深入理解卷积

Posted 2023-03-19 天空天空sky

一、深入理解积分

\\[\\int_ - \\infty ^\\infty  f\\left( t \\right) dt\\]

\\[\\sum\\nolimits_ - \\infty ^\\infty  f(t)  \\cdot 1\\]

       对比积分和求和可知，积分就是连续版本的求和，或者更本质的说，积分就是求和。

二、深入理解卷积

       连续形式：

\\[\\left( f * g \\right)(n) = \\int_ - \\infty ^\\infty  f(t)g(n - t)dt \\]

　　离散形式：

\\[\\left( f * g \\right)(n) = \\sum\\nolimits_ - \\infty ^\\infty  f(t)g(n - t) \\]

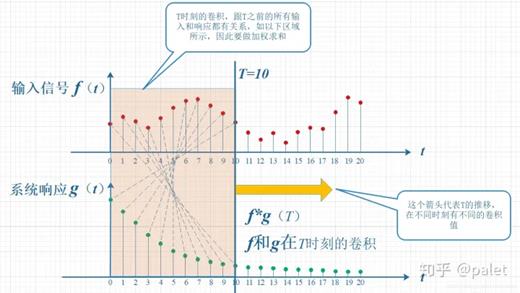
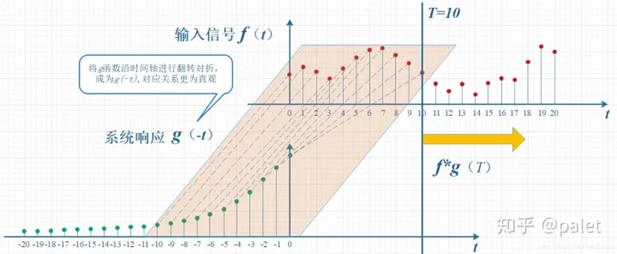
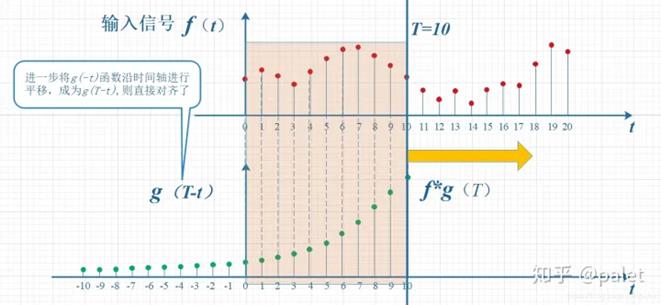
       “卷”：先对g函数进行翻转，然后再把g函数平移到n。

       “积”：对两个函数的对应点相乘，然后求和。或者看成对f进行加权(g)求和。

 

       整体看来是这么个过程：

　　翻转——>滑动——>叠加——>滑动——>叠加——>滑动——>叠加.....

　　多次滑动得到的一系列叠加值，构成了卷积函数。

三、应用场景

　　1. 信号分析

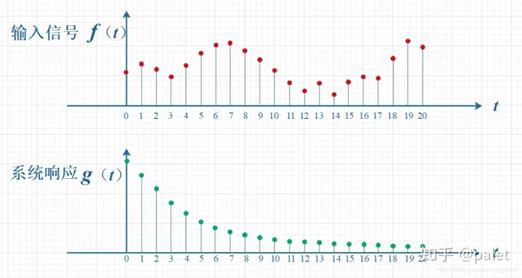
　　2. 图像处理(例如卷积神经网络)

       实际在计算的时候，都是用翻转以后的矩阵（或者理解成省略了翻转步骤），直接求矩阵内积。

四、参考资料

1.知乎. Tetradecane. 《如何通俗易懂地解释卷积？》. https://www.zhihu.com/question/22298352/answer/637156871