卷积神经网络结构——LeNet-5(卷积神经网络入门,Keras代码实现)
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了卷积神经网络结构——LeNet-5(卷积神经网络入门,Keras代码实现)相关的知识,希望对你有一定的参考价值。
参考技术A 要深入理解卷积神经网络的结构,我们需要追根溯源,只有这样才能更好的理解 CNN 网络。1998年 LeCun 和 Bengio 等人利用 LeNet-5 网络在手写体数字识别领域上的识别效果超过了传统方法,从此开启了卷积神经网络的在图像上的应用大门。据说,一开始美国银行的手写体数字识别就是用的这个算法。
Gradient -Based Learing Applied to Document Recognition
http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf
论文有点长,46页,估计很难读下来。
LeCun 做了一些网页展示,有兴趣可以去浏览。
http://yann.lecun.com/exdb/lenet/
https://github.com/uestcsongtaoli/LeNet-5
上图是 LeCun 原论文中 LeNet-5 的结构图。
卷积神经网络03-1 AlexNet网络结构与原理分析
戳一戳!和我一起走进深度学习的世界
导读
之前,我们学习了LeNet,我想大家应该还是有比较深刻印象的,作为卷积神经网络的鼻祖,它为卷积神经网络的发展起到了非常重要的作用,我们今天要讲的AlexNet是LeNet的进化版本。
今天要分享这篇文章带我们一起了解LeNet存在的问题,AlexNet做了哪些改进,AlexNet的特点,AlexNet结构详细介绍及分析。
如果你想深入了解AlexNet对应的论文翻译,可以看这篇文章:
如果你想更加深入了解技术讲解,那就让我们走进这篇文章,一起来了解一下吧!如果你有什么问题,或者有什么想法,欢迎评论与我一起沟通交流。
1 温故知新
1 LeNet的网络结构
从这篇文章开始,我们就要深入学习一个新的卷积神经网络模型了。
在学习之前,我们先来回顾一下上次讲到的LeNet网络,LeNet-5是比较简单的卷积神经网络,结构较为简单,一个完整的结构图如下:
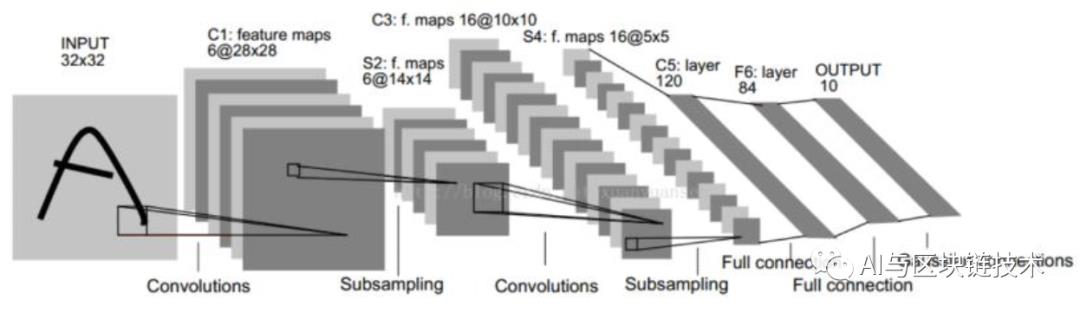
LeNet-5的网络结构
不考虑输入层,一个LeNet网络 如下7层:
C1卷积层
S2池化层
C3卷积层
S4池化层
C5卷积层-全连接层
F6全连接层
输出层-全连接层
所以,其实我们看卷积神经网络也很简单,无非就是卷积-池化-全连接的排列组合。
2 LeNet的弊端
作为第一个提出来的卷积神经网络,LeNet有及其重要的意义,但是这也免不了,它也是存在一定问题的。
第一个就是激活函数的问题,LeNet中使用的是Sigmoid函数,这个函数虽然可以将线性转化为非线性,但是Sigmoid函数有很大的问题,我们也专门用一篇文章来讲了各种各样的激活函数,讲了他们的优缺点。具体内容,大家可以看下面的文章:
第二就是模型太过简单,只有7层,提出的时候,只是解决了十个手写数字,虽然也能用在ImageNet数据集上,但是结果有点感人。
当然这个是客观评价LeCun大神的LeNet,还是让我们膜拜一下大神!
2 AlexNet 简介
我们回顾完了,我们先来看了解AlexNet。
虽然第一个典型的CNN是LeNet5网络结构,但是第一个引起大家注意的网络却是AlexNet,也就是文章《ImageNet Classification with Deep Convolutional Neural Networks》介绍的网络结构。
1 ImageNet
要说AlexNet,最先说的,我觉得应该是ImageNet,或者说是李飞飞大神。

李飞飞教授
李飞飞教授应该算是计算机视觉领域中最著名的华人科学家之一。2009年,李飞飞教授等在CVPR2009上发表了一篇名为《ImageNet: A Large-Scale Hierarchical Image Database》的论文,从此开启了深度学习-计算机视觉的新世界。
这个和我们今天的文章有什么关系呢?了解AlexNet的同学都知道,AlexNet能引发卷积神经网络的大潮,就是因为AlexNet在2012年的ImageNet大赛上获得了冠军。
遥想那一年,我还在考虑世界末日,是不是真的要来了。
2 作者介绍
先来欣赏一下三位作者的容颜:

本文的一作,Alex Krizhevsky,这个网络的名字就是用他的名字命名的,网上有关于他的介绍比较少,可能大牛就是这样,只给我们留下一个英俊的背影,和一篇惊世巨作。
二作Ilya Sutskever,还是比较出名的,因为他是OpenAI的联合创始人,有人称他为计算机视觉、机器翻译、游戏和机器人的变革者。
三作,可以说是幕后的大佬了,Geoffrey E. Hinton(杰夫·欣顿)教授,别人尊称他为“神经网络之父”,因为是他将“深度学习”从边缘课题变成了我们现在最火热的计算机技术之一,正是他多年如一日的坚持,才让曾经不被看好的神经网络成为主流,当然不可否认的是,能成为主流的一个重要原因是计算机硬件的飞速发展促进了算力的极大提升。上面提到的两位大牛,都是杰夫·欣顿教授的弟子。
3 原作
大家也可以通过下面的链接下载原作先拜读一下。
https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
2 AlexNet 结构层次
了解了Alex的一些情况之后,我们先来看一下它的结构层次,等我们对AlexNet有个比较深刻的了解之后,我们再分析它的一些特点。
首先我们先来看一下AlexNet整体的结构层次
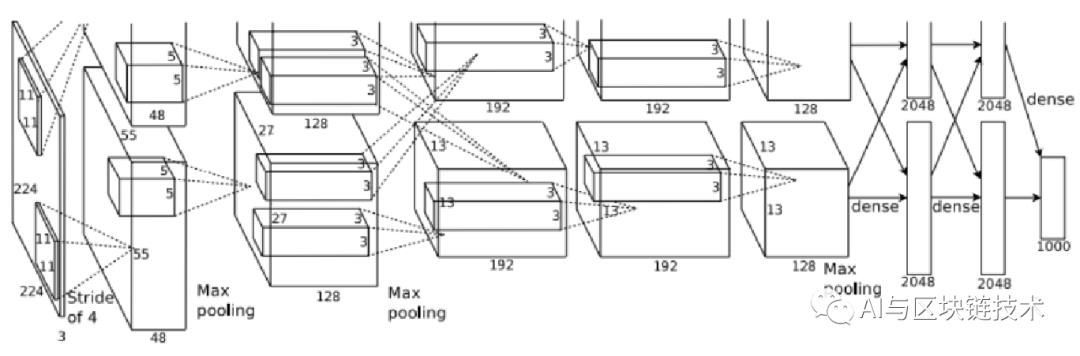
AlexNet结构
总体来看,AlexNet分为了上下两部分,这个是因为AlexNet网络中使用了两块GPU进行协作训练,这样可以大幅度提高效率,到了后面会进行交互。
AlexNet使用了除输入层外的八层结构,前五层以卷积层为核心,后三层以全连接层为核心,接下来我们一层一层分析。
1 输入层
AlexNet解决的是彩色图像的分类问题,彩色图像的深度是3,对应红蓝绿三种颜色。
图像的尺寸为224×224的正方形。但是在具体的计算过程中,输入图像的尺寸变为了227×227,这个是为了方便后面的操作。
为什么要改成227呢,让我们在第一层详细分析一下吧!
2 第一层
第一层是多个操作的集合,第一层如下图:
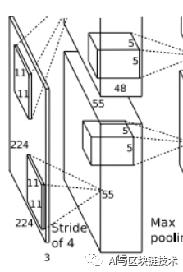
该层的处理流程是:
卷积-->ReLU-->池化-->归一化。
在AlexNet网络中,卷积核的大小为11×11×3。这个时候,卷积操作的步长不再是1了,而是变成了4,这样我们就会得到一个55×55×1的特征图,在第一层中有96个卷积核,分两个GPU,所以每个GPU就会有55×55×48的特征图。
这个时候,我们就要考虑两个问题了:
1.为什么要把224改为227?
2.55是如何计算的?
有人说,是因为:(227-11)/4+1=55
而且很多文章都是这样说明的。具体原因不得而知。但真实原因不是这样的,首先希望大家能够看一下下面的文章,先了解一下相关的原理及计算方法,然后我们再往下看。
对于一个n×n×3的图像,经过卷积核为m×m×3,步长为s的卷积运算,满足什么条件,图像的所有像素才会参与卷积运算?
我们知道结论如下:
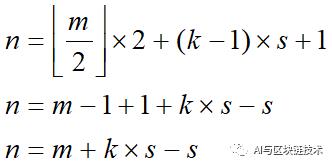
现在n=224,m=11,s=4,则:
但是:
也就是说,参与运算的只有219×219的图像,那想要保证所有的都参与运算,还可以再在行列方向各走两个步长,即再增加8,即为227。
那为什么是走两个步长呢?
我们既要保证所有的都参与运算,还要保证,尽可能少扩展边缘,也就是说,最后的情况要选择大于等于当前尺寸中满足条件的最小值。走一个步长不够,走三个步长过了。所以我们再多走两个步长。
多走两个步长,则一共走了55个步长,最后生成的特征图的尺寸为55×55。
然后我们知道有96个卷积核,并且要分到两个GPU进行训练,则生成的最终特征图尺寸为:
经过卷积操作后,我们就要执行线性整流操作,使用ReLU函数对得到的结果进行处理,这一步操作就是激活函数操作,具体有关于激活函数请看:
再下一步就是池化操作,这里的池化是重叠池化,因为池化的区域大小为3×3,而步长为2。AlexNet采用的是最大池化。使用最大池化而不是平均池化的目的是为了避免平均池化的模糊化效果,从而保留最显著的特征。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖。
在池化操作中,具体的计算方法和卷积操作的原理是一致的,所以我们有:
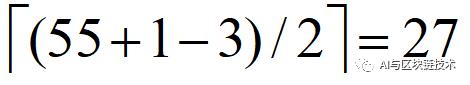
为什么是向上取整呢?给大家看一张图就明白了:
即我们池化后生成的特征图大小为
一般的池化层因为没有重叠,即池化尺寸和步长一般是相等的,而在AlexNet中步长小于池化尺寸,这就会导致一些像素会参与很多池化操作,这样的目的是为了提升特征的丰富性,减少信息的丢失,从而可以减少过拟合。
最后就是局部响应归一化操作,目的是为了提高准确度。
总结一下,在这一层中:
输入图片尺寸:224×224×3(扩展为227×227×3)
卷积核大小与步长:11×11×3 / 4
卷积核个数:96(分两部分)
卷积后特征图大小:55×55×48*2
池化大小与步长:3×3 / 2
池化后特征图大小:27×27×48*2
3 第二层
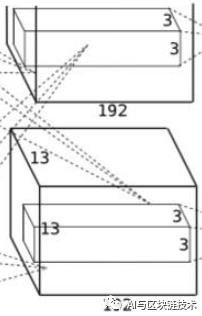
第二层是第一层的继续,第二层如下图:
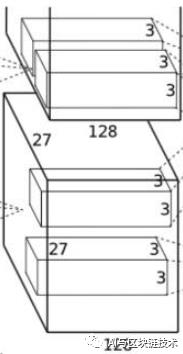
第二层的操作如下:
卷积-->ReLU-->池化-->归一化。
第二层的输入就是第一层的输出。即输入为:
第二层使用256个5×5×48的卷积核,即卷积核为:
卷积步长为1,在这里作者使用了四边各2像素的边缘填充(扩展),这样就能保证卷积后图像行列尺寸不会改变:
所以卷积后的特征图为:
然后再做最大池化,池化尺寸还是3×3,池化步长还是2,池化后为:
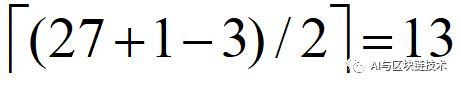
所以池化后的特征图为:
总结一下,在第二层中:
输入特征图:27×27×48*2(四边做两像素的边缘填充)
卷积核大小与步长:5×5×48 / 1
卷积核个数:256(分两部分)
卷积后特征图大小:27×27×128*2
池化大小与步长:3×3 / 2
池化后特征图大小:13×13×128*2
4 第三层
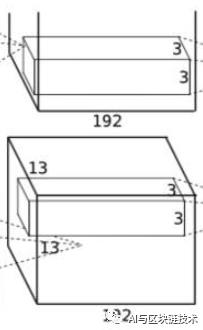
第三层是第二层的继续,第三层如下图:
第三层的操作如下:
卷积-->ReLU
第三层的输入就是第二层的输出。即输入为:
第三层使用384个3×3×128的卷积核,即卷积核为:
卷积步长为1,跟上面原理一样,在这里作者使用了四边各1像素的边缘填充(扩展),这样就能保证卷积后图像行列尺寸不会改变,所以卷积后的特征图为:
第三层没有后续的池化操作。
总结一下,在第三层中:
输入特征图:13×13×128*2(四边做一像素的边缘填充)
卷积核大小与步长:3×3×128 / 1
卷积核个数:384(分两部分)
卷积后特征图大小:13×13×192*2
5 第四层
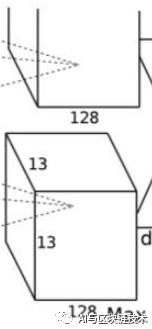
第四层是第三层的继续,第四层如下图:
而且第四层和第三层十分类似,具体的区别就在于第三层上下两个GPU训练的会进行特征图的特征融合,而第四层没有做特征融合,只在GPU内部进行操作。
第四层的操作如下:
卷积-->ReLU
第四层的输入就是第三层的输出。即输入为:
第三层使用384个3×3×192的卷积核,即卷积核为:
卷积步长为1,跟上面原理一样,在这里作者使用了四边各1像素的边缘填充(扩展),这样就能保证卷积后图像行列尺寸不会改变,所以卷积后的特征图为:
第四层没有后续的池化操作。
总结一下,在第四层中:
输入特征图:13×13×192*2(四边做一像素的边缘填充)
卷积核大小与步长:3×3×128 / 1
卷积核个数:384(分两部分)
卷积后特征图大小:13×13×192*2
6 第五层
第五层是第四层的继续,第五层如下图:
第五层的操作如下:
卷积-->ReLU-->池化
第五层的输入就是第四层的输出。即输入为:
第五层使用256个3×3×192的卷积核,即卷积核为:
卷积步长为1,跟上面原理一样,在这里作者使用了四边各1像素的边缘填充(扩展),这样就能保证卷积后图像行列尺寸不会改变,所以卷积后的特征图为:
第五层采取了和前面一样的池化操作,采用最大池化,池化核为3×3,步长为2。
则我们最终会得到的特征图为:
总结一下,在第五层中:
输入特征图:13×13×192*2(四边做一像素的边缘填充)
卷积核大小与步长:3×3×192 / 1
卷积核个数:256(分两部分)
卷积后特征图大小:13×13×256*2
池化大小与步长:3×3 / 2
池化后特征图大小:6×6×128*2
7 第六层
第六层如下图:

第六层的操作如下:
全连接-->ReLU-->Dropout
第六层的输入就是第五层的输出。即输入为:
然后第六层使用4096个6×6×128的全连接核与输入进行全连接运算,即全连接核为:
全连接核和卷积核其实就是一个多维矩阵,本质上是一样的,卷积核只针对某个范围进行特征提取,不断形成特征图,而全连接核是针对特征图中的所有像素进行运算。全连接后后的特征图为:
即最后只有4096个神经元,分为两组,每组由2048个神经元构成一列。
从这一层开始引入Dropout,在这里,先暂时不具体讲解,后面我们专门写一篇文章,来说明Dropout,目前我们只需要知道的就是Dropout可以通过让某些神经元不工作来减少过拟合问题。
总结一下,在第六层中:
输入特征图:6×6×128*2
全连接核大小:6×6×128
全连接核个数:4096(分两部分)
全连接后大小:1×1×2048*2
8 第七层
第七层和第六层很类似,第七层如下图:
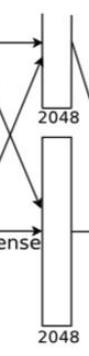
第七层的操作如下:
全连接-->ReLU-->Dropout
很多文章并没有把第七层讲明白,只是说前后全连接,至于如何全连接,并没有讲清楚。
第七层的全连接核第六层的全连接是不同的。
第六层的全连接是卷积操作,所以,我们也会把第六层的全连接称之为卷积全连接。
但是第七层做的是线性变换,即矩阵运算。
这两个具体有什么区别呢?
卷积就是简单地对应位置相乘最后再相加(求平均)。卷积不能算作矩阵运算。
全连接是矩阵乘积,而又因为,全连接层是1×1×n的,所以计算过程也是线性变换的过程。
但这两者又是可以转化的!
如果把第六层的拉长为一个1×1×n的,那么这个也可以算作是矩阵运算。但是要给参数w进行转置。
第七层输入为:
第七层经过全连接输出为:
总结一下,在第七层中:
输入特征图:1×1×2048*2
输出特征图:1×1×2048*2
8 第八层
第八层如下图:
第八层和第七层是类似的,他们进行的操作都是矩阵运算。而且他们都包括如下操作:
全连接-->ReLU-->Dropout
不同点在于输出不同,第八层最后输出的是1000个神经元。这个1000是所有的能识别的类别个数,这1000个神经元的值是每种类别可能的概率。
3 AlexNet 分析
讲完了AlexNet结构层次,我们来分析一下AlexNet。
1 使用ReLU激活函数
在AlexNet中首次使用了AlexNet函数,相比较LeNet中使用的Sigmoid函数,ReLU操作更加简单粗暴,一方面能够加快运算速度,另一方面,不会存在正值的梯度消失问题。
当然ReLU也有其自己的缺点,具体想了解激活函数的优缺点对比,就看下面这篇文章吧:
2 多GPU训练
作为第二个知名卷积神经网络(LeNet是第一个),一上来就使用双GPU,确实猛!!!
不由得想给个双击666,大赞!
说正经的,这个想法为后面的分布式深度学习提供了很好的借鉴作用。
双GPU极大的提升了训练效率,以更短的时间得到了更高的准确率。
3 局部响应归一化
局部响应归一化被用来增强泛化能力,有助于模型快速收敛并提高准确度。
局部响应归一化是仿造生物学中活跃的神经元对相邻神经元的抑制现象。这个思路是很对的,因为深度学习就是在模拟人的神经网络。
但是后面再VGG中,发现是否使用局部响应归一化对准确率并没有太大帮助,使用了局部响应归一化的模型并没有在准确率上得到提升。所以,局部响应归一化具体有没有用,在什么时候有用,怎么样改变更有用,还有待考证。
在我看来,局部响应归一化对于AlexNet有用,而对VGG模型没用,可能是因为AlexNet本身模型准确度比较差,而局部响应归一化能提升一定的准确度,所以效果较为明显。而对于VGG来说,模型相对准确度很高了,局部响应归一化的提升在VGG面前“不值一提”。所以就在VGG里被摒弃了吧!
4 多种方式减少过拟合
在AlexNet中使用了很多种方式减少过拟合问题。我们在这里统一说明。
减少过拟合一共使用了如下几种方式:
重叠池化数据增强Dropout
重叠池化可以使某一个像素值影响到多个最终生成的像素。重叠池化的目的我们前面也讲过了,是为了提升特征的丰富性,减少信息的丢失,从而可以减少过拟合。
数据增强,这一步是在输入数据时做的操作,数据增强是通过对数据做变换来强化数据中的一些重要特征,从而更好地被提取,减少过拟合。
Dropout是Hinton中提出的,这种方法会暂时屏蔽掉某些神经元,使得这些神经元不参与运算,这样的一个直接好处是,极大的减少运算量。而通过减少这些神经元的作用,能够阻止某些特征检测器之间的相互作用,减少过拟合的情况。
4 说在后面的话
AlexNet真正让深度学习走到舞台中央,至此以后,深度学习开始了蓬勃发展。
希望大家能够通过今天这篇文章,了解AlexNet原理,了解AlexNet中一些思想,能够在以后的学习研究中给自己一些启发。
后续,我们会专门再用一篇文章来讲解代码实战。也感谢大家一直以来的支持,我会一直努力,为大家带来好的文章,让我们一起努力,共同营造一个好的学习和科研氛围吧!
AI与区块链技术
长按二维码关注
如果喜欢这篇文章
麻烦给我一个在看
以上是关于卷积神经网络结构——LeNet-5(卷积神经网络入门,Keras代码实现)的主要内容,如果未能解决你的问题,请参考以下文章