深入浅出图神经网络|GNN原理解析☄学习笔记卷积神经网络
Posted 白鳯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深入浅出图神经网络|GNN原理解析☄学习笔记卷积神经网络相关的知识,希望对你有一定的参考价值。
《深入浅出图神经网络》GNN原理解析☄学习笔记(三)卷积神经网络
文章目录
卷积神经网络(Convolutional Neural Network,
CNN或
ConvNet)是一种具有局部连接、权值共享等特点的前馈神经网络,在图像和视频分析领域,比如图像分类、目标检测、图像分割等各种视觉任务上取得了显著的效果,是目前应用最广泛的模型之一。
卷积与池化
信号处理中的卷积
卷积的一个典型应用是:针对某个线性时不变的系统,给定输入信号f(x)和系统响应g(τ),求系统的输出:
(
f
∗
g
)
(
t
)
=
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
(f*g)(t)=\\int_-∞^∞f(τ)g(t-τ)
(f∗g)(t)=∫−∞∞f(τ)g(t−τ)
卷积定理:它的意义在于可以将时域中复杂的卷积运算转换为频域中简单的相乘运算,即
(
f
∗
g
)
(
t
)
等
价
于
F
(
w
)
G
(
w
)
(f*g)(t)等价于F(w)G(w)
(f∗g)(t)等价于F(w)G(w)
要理解卷积,需要先知道傅里叶变换。傅里叶变换是将时域中的数据转换到频域中的一种方法,它将函数分解为一系列不同频率的三角函数的叠加,可以将它理解为从另一个维度去观察数据。
单通道卷积
H m , n = ∑ i = − k 2 k 2 ∑ j = − k 2 k 2 X m + i , n + j ⋅ G i , j H_m,n=\\sum_i=-\\frack2^\\frack2\\sum_j=-\\frack2^\\frack2X_m+i,n+j·G_i,j Hm,n=i=−2k∑2kj=−2k∑2kXm+i,n+j⋅Gi,j
其中,k/2是下取整的,G是卷积核。
通常将卷积得到的输出为特征图(feature map)。
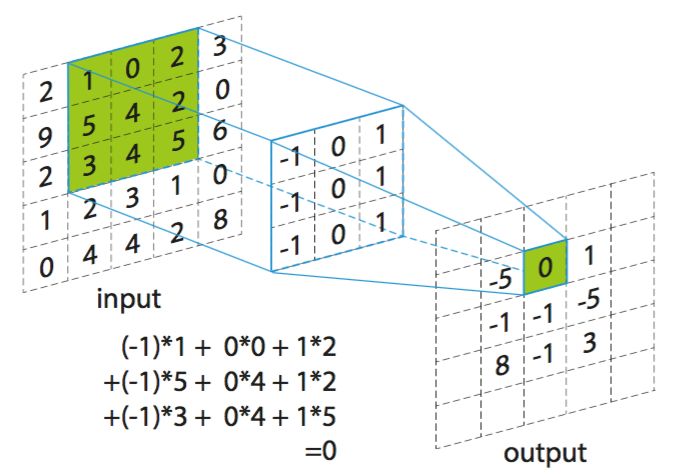
图片来源于:https://pic2.zhimg.com/v2-61e5fa30572aa4e8bd6f88518d7364c8_1200x500.jpg
在上图的例子中,输入维度在卷积之后减小了,这是由于输入的边界导致的,卷积的起始位置无法取到输入的每一个位置。这会带来以下两个问题:
- 当进行多次卷积运算后,输出的尺寸会越来越小;
- 越是边缘的像素点,对于输出的影响越小,因为卷积运算在移动到边缘的时候就结束了。中间的像素点会参与多次计算,但是边缘的像素点只会参与一次运算,导致了
边缘信息的丢失。
为了解决上述问题,通常对边缘使用0值进行填充(padding)
有时在计算时,不必对每个位置进行计算,可以每隔几个位置计算一次,这个间隔称为步长(stride)。
多通道卷积
假 设 输 入 X ∈ R H × W × C , C 表 示 通 道 数 ( c h a n n e l s ) , 卷 积 核 的 长 宽 都 为 k 假设输入X∈R^H×W×C,C表示通道数(channels),卷积核的长宽都为k 假设输入X∈RH×W×C,C表示通道数(channels),卷积核的长宽都为k
k × k 的 卷 积 核 构 成 G c ′ ∈ R k × k × C k×k的卷积核构成G^c'∈R^k×k×C k×k的卷积核构成Gc′∈Rk×k×C
H m , n , c ′ = ∑ i = − k 2 k 2 ∑ j = − k 2 k 2 X m + i , n + j , : ⋅ G i , j , : c ′ H_m,n,c'=\\sum_i=-\\frack2^\\frack2\\sum_j=-\\frack2^\\frack2X_m+i,n+j,:·G_i,j,:^c' Hm,n,c′=i=−2k∑2kj=−2k∑2kXm+i,n+j,:⋅Gi,j,:c′
多通道卷积的过程可以看做一个3D的卷积核滑过输入层。
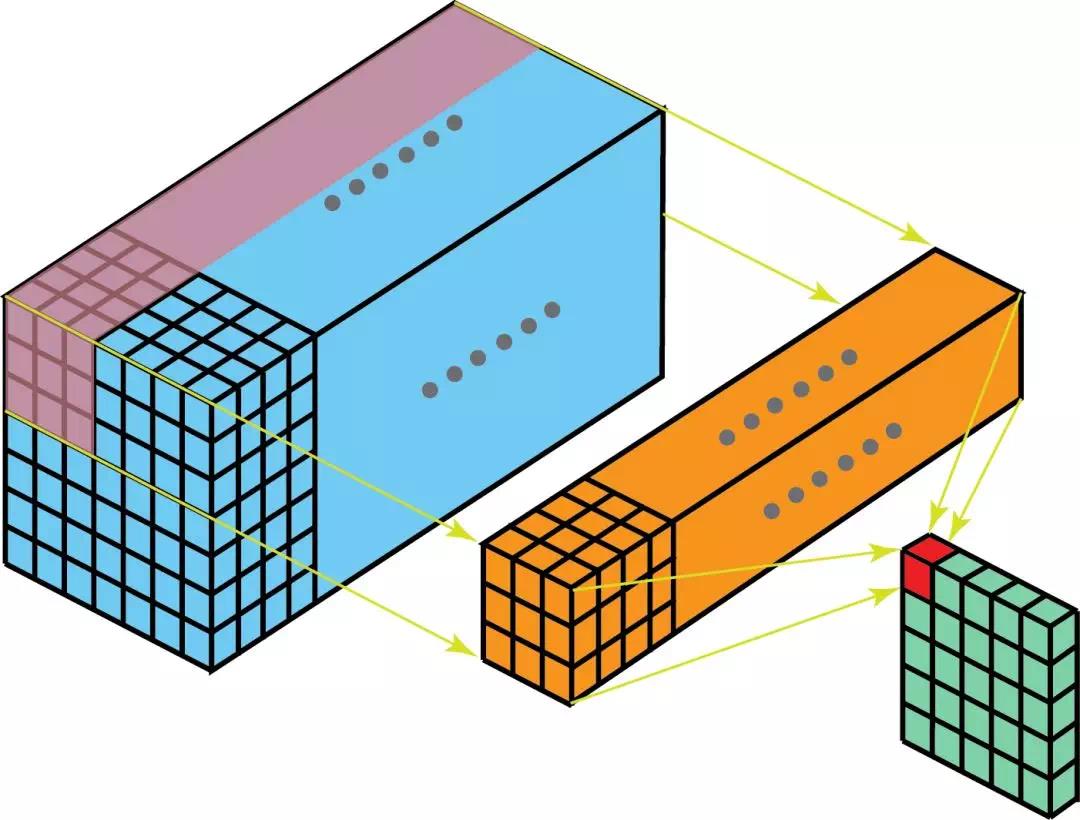
图片来源于:http://xukeqiniu.xukeai.cn/9a56f1208b252c44913367ce9754a392.png
卷积完成后,通常会为每个特征图加一个偏置。
池化
池化的主要目的是降维,以降低计算量,并在训练初期提供一些平移不变性。常用的两种池化操作是平均池化和最大值池化。
池化操作就是使用一个固定大小的划窗在输入上滑动,每次将划窗内的元素聚合为一个值作为输出。根据聚合方式的不同,可以分为平均池化和最大值池化。
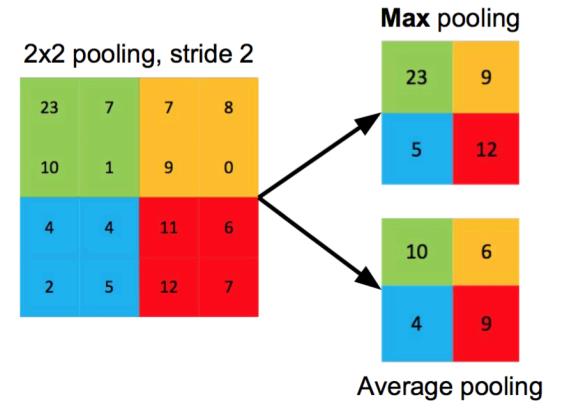
图片来源于:http://xukeqiniu.xukeai.cn/9a56f1208b252c44913367ce9754a392.png
假设输入维度为HxWxC,卷积核的大小为k,填充值为p,步长为s,输出的特征图为H’xW’xC’,那么它们之间的关系可以通过下式给出,W’的计算方式也相同:
H
′
=
H
+
2
p
−
k
s
+
1
H'=\\fracH+2p-ks+1
H′=sH+2p−k+1
卷积神经网络
卷积神经网络是通过将卷积层与池化层进行堆叠得到的。
AlexNet结构
卷积神经网络的结构一般可以分为两个部分:一部分是由卷积层和池化层交替堆叠构成的骨干网络,它主要用于从输入层提取丰富的特征;另一部分是全连接层,它将卷积得到的特征图展开,也就是说丢弃了特征图的空间信息,它的主要作用是聚合全局信息并将其映射到输出空间。
卷积神经网络的特点
卷积神经网络具有以下3个特点:局部连接、权值共享、层次化表达
-
局部连接
由于图像通常具有局部相关性,因此卷积计算每次只在与卷积核大小对应的区域进行,也就是说输入和输出是局部连接的。
-
权值共享
在图像中,不同的区域使用相同的卷积核参数,这一方面减少了参数量,另一方面带来了平移不变形。
-
层次化表达
卷积网络通过卷积层堆叠得到,每一层都是对前一层进行变换,提取的特征从底层次到高层次,逐渐变得抽象。
特殊的卷积形式
1x1卷积
卷积核的大小为1,通常1x1卷积有以下功能:一是用于信息聚合,同时增加非线性,1x1卷积可以看做是对所有通道的信息进行线性加权,即信息聚合,同时,在卷积之后可以使用非线性激活函数,可以一定程度地增加模型的表达能力;二是用于通道数的变换,可以增加或者减少输出特征图的通道数。
转置卷积
转置卷积(Transposed Convolution),它是语义分割任务中必不可少的模块。语义分割指的是对图像在像素级别上进行分类,属于同一类别的像素常对应着某个目标。
基于CNN的语义分割模型通常由都由两部分组成,一部分是编码器,用于将原始的输入图像映射到某个低维的特征空间中,它既需要编码目标的特征信息,也要编码位置信息,以正确地预测每个像素位置的类别。另一部分是解码器,它将编码的低维特征映射回像素空间,已对每个像素的具体类别进行判断。
解码器部分我们无法使用前面介绍的标准卷积,因为前面的卷积操作不会使得特征图的长宽维度增加,而转置卷积则相反,它可以完成长宽维度的增加,将编码的低维特征逐步映射回像素空间。
对于转置卷积 中输入维度、卷积核大小、填充以及步长与输出维度的关系,可以通过下式来确定:
H
′
=
s
(
H
−
1
)
−
2
p
+
k
H'=s(H-1)-2p+k
H′=s(H−1)−2p+k
空洞卷积
空洞卷积(Dilated Convolution)通过在卷积核元素之间插入空格来“扩张”卷积核,其中有个超参数用于控制扩张的程度,称为空洞率r(dilation rate),指的是在卷积核中插入r-1个0,因此对于原先大小为k的卷积核,在使用空洞卷积之后实际的卷积核大小变为k+(k-1)(r-1)。由于卷积核扩大,感知野也会扩大。因此空洞卷积是一种不断增加参数量而可以快速扩大感知野的有效方式。
分组卷积
分组卷积最早是在AlexNet中出现的,当时训练AlexNet时卷积操作不能全部放在同一个GPU中进行处理,因此作者把特征图分给了多个GPU来处理,最后再把多个GPU的处理结果融合,这实际上就是分组卷积。
可减少参数量。
深度可分离卷积
深度可分离卷积由两部分组成,一部分是沿着深度的逐层卷积,另一部分是1x1卷积。
深度可分离卷积相比较于标准卷积,不仅减少了参数量,而且可以降低计算量、提高运算效率,因此这类卷积通常用于对速度有要求的卷积结构设计中。
参考资料:《深入浅出图神经网络》GNN原理解析
以上是关于深入浅出图神经网络|GNN原理解析☄学习笔记卷积神经网络的主要内容,如果未能解决你的问题,请参考以下文章