照片重复取样法计算原理

Posted 2023-05-13

参考技术A 重组计算原理。
图像重采样是指对采样后形成的由离散数据组成的数字图像按所需的像元位置或像元问距重新采样,以构成几何变换后的新图像。重采样过程本质上是图像恢复过程,它用输入的离散数字图像重建代表原始图像二维连续函数,再按新的像元间距和像元位置进行采样。其数学过程是根据重建的连续函数(曲面),用周围若干像元点的值估计或内插出新采样点的值。图像重采样在图像处理中应用非常广泛，如SIFT特征提取。图像重采样后图像的维数会发生改变。当重采样图像小于原图像维数时，称为降采样；当重采样图像维数大于原图像时，称为升采样。VTK中可以方便的对图像进行重采样。vtkImageShrink3D类实现图像降采样。降采样需要设置每个方向的采样率，降采样率越大，图像越模糊。升采样的原理与降采样原理一致，只是增加采样点数来增加图像的维数。VTK中vtkImageMagnify来实现图像的升采样。

[数学建模]蒙特卡罗方法

1.概念

蒙特卡罗方法（随机取样法）是一种计算方法。原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。

2.两个应用例子

例子1：求π的值。

正方形内部有一个相切的圆，它们的面积之比是π/4。现在，在这个正方形内部，随机产生1000000个点（即1000000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。

 

MATLAB实现：

N=1000000;    %随机点的数目

x=rand(N,1);  %rand 生成均匀分布的伪随机数。分布在（0~1）之间

y=rand(N,1);  %矩阵的维数为N×1

count=0;

for i=1:N

   if (x(i)^2+y(i)^2<=1)

     count=count+1;

    end

end

PI=4*count/N

例子2：计算积分

计算函数 y = x^2 在 [0, 1] 区间的积分，就是求出红色曲线下面的面积。这个函数在 (1,1) 点的取值为1，所以整个红色区域在一个面积为1的正方形里面。在该正方形内部，产生大量随机点，可以计算出有多少点落在红色区域（判断条件 y < x^2）。这个比重就是所要求的积分值。

 

 

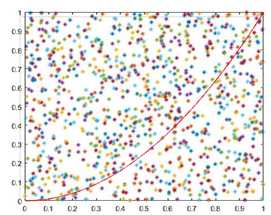
MATLAB实现：

clear

clc

N=10000;  

x=rand(N,1); 

y=rand(N,1);

count=0;

for i=1:N

   if (y(i)<=x(i)^2)

     count=count+1;

   end

end

result=count/N

3. 与拉斯维加斯方法的比较

（1）蒙特卡罗算法：假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。——尽量找好的，但不保证是最好的。

特点：采样越多，越近似最优解；

（2）拉斯维加斯方法：假如有一把锁，给我100把钥匙，只有1把是对的。于是我每次随机拿1把钥匙去试，打不开就再换1把。我试的次数越多，打开（最优解）的机会就越大，但在打开之前，那些错的钥匙都是没有用的。——尽量找最好的，但不保证能找到。

特点：采样越多，越有机会找到最优解。

4.更深度的应用

蒙特卡洛树搜索---深度学习，强化学习