matlab稀疏矩阵

Posted 2023-05-11

用maltab稀疏矩阵函数表示

%% 方法一
Ai = [1 2 2 3 3 4]; %列索引
Aj = [1 1 2 2 3 3]; %行索引
As = [15 2 15 2 15 2]; %对应索引元素
Am = 4;  %矩阵列
An = 3;  %矩阵行
A = sparse(Aj,Ai,As,An,Am)
full(A)
%% 方法二（题意应该是用该方法，因为对角线有明显规律）
BD =[15 2;15 2;15 2];  %对角线元素
Bp = [0 1];  %对角线个数，0-主对角线，1-向上移对角线，-1-向下移
Bm = 3;  %矩阵行
Bn = 4;  %矩阵列
B = spdiags(BD,Bp,Bm,Bn)
full(B)

参考技术A sparse([1 1 2 2 3 3],[1 2 2 3 3 4],[1.5 2 1.5 2 1.5 2],3,4)

图像去噪基于matlab稀疏表示KSVD图像去噪含Matlab源码 2016期

一、低秩稀疏图像重建简介

1 矩阵的低秩稀疏分解理论
从数学上讲, 矩阵的秩反应了矩阵的固有属性, 矩阵的低秩性是指矩阵的秩相对于矩阵的行数和列数而言很小.低秩矩阵稀疏分解模型是将已知矩阵M (M∈Rm×n) 分解为一个低秩矩阵部分L (L∈Rm×n, rank (L) ≤m, n) 和一个稀疏矩阵部分S (S∈Rm×n) , 即M=L+S.

其优化问题描述如下:

其中, ‖L‖*表示矩阵L的核范数即L的奇异值之和, ‖S‖1表示矩阵的1范数即S每一列元素绝对值之和的最大值.该问题的求解采用文献中介绍的目前最有效的增广拉格朗日乘子法 (exact augmented Lagrangian method, EALM) 求解.

2 图像的稀疏表示模型
2.1 信号的稀疏表示
信号的稀疏是指在某些变换域内, 信号的大多数变换系数为零或者绝对值很小, 只有少部分变换系数的绝对值较大, 我们就认为信号是稀疏的.信号的稀疏性被广泛应用于数据压缩、通信以及视频图像处理领域.

在变换域字典D∈Rn×K (n≤K) 下, y∈Rn表示为字典原子的稀疏线性组合, 系数向量α∈Rn是稀疏的, 则信号的稀疏表示问题可以描述为:

其中, l0范数计算的是α中非零元素的个数, 这是一个非凸问题.可以将其凸松弛为l1范数, 则信号的稀疏表示问题可以表示为如下的凸优化问题:

2.2 基于稀疏表示模型的超分辨率重建
目前最有效的基于稀疏表示的超分辨率重建算法是由Yang等人提出并改进的双字典学习算法.该方法的基本思想是:首先训练样例中的HR图像和对应的LR图像得到一对HR字典和LR字典;然后利用LR字典求解LR图像块的稀疏表示系数;最后利用HR字典和这个稀疏系数来重建对应的HR图像块.

将高分辨率图像x降质为低分辨率图像y的模型表示如下：

其中, S表示下采样处理, H表示模糊处理, n代表噪声向量.
用Dh表示由一组高分辨率图像样本训练得到的过完备字典, 在Dh下, x的稀疏表示为α, 其式子表达如下:

但是式 (6) 是一个NP-hard问题, 凸优化为L1范数最小化问题表示如下:

由图像的降质模型可得到相应的低分辨率图像块表示为:

根据优化理论, 对低分辨率图像块进行稀疏表示的优化过程可描述为:

其中, ‖y-Dlα‖22≤ξ为重建高分辨率图像块与输入低分辨率图像块的匹配程度的一个约束.根据对应的高、低分辨率图像块在字典对下有相同的稀疏表示, 则通过^x=Dhα即可重建出高分辨率图像^x.通过图像融合技术可进一步得到完整的高分辨率图像.

3 基于低秩约束和字典学习的重建方法
3.1 初步重建
将图像的观察模型表示为:Xl=SBXh+n, 建立从观察到的低分辨率图像Xl重建出高分辨率图像Xh的问题模型:

图像的超分辨率重建问题具有不适定性, 为此我们需要挖掘更多的图像先验信息解决这一问题.图像的非局部自相似性就是指的自然图像自身所蕴含的先验知识, 它是指在一副自然图像中会存在一些重复或相似的微结构, 这种特性称为图像的的非局部自相似性.对低分辨率图像Xl进行分块, 进行块重叠提取操作, 对于图像中的一个图像块pl0∈Rm×n, 通过块匹配的方法在图像中可以为其提取s个相似块pi0, pi1, …pic.将这些相似的图像块排成矩阵Pi∈Rm×n× (c+1) , 由矩阵列向量间的相关性分析我们知道, 矩阵Pi具有天然的低秩性或近似低秩的性质.将图像的自相似性先验信息引入模型 (10) 得到矩阵低秩约束下的图像重建模型:

Ei表示从图像Xh中提取相似图像块的操作.式 (11) 第二项采用核范数‖·‖*计算矩阵的秩, 即为图像Xh中全部N个小块对应的非局部自相似矩阵的秩总和.

在矩阵Pi中, 不同的图像块与pi0的相似程度不同, 为了充分利用这些图像块间非局部相似先验信息的有效性, 我们引入权重矩阵Wi表征不同图像块间的相似程度.这里图像块之间的相似度一般通过他们之间的欧几里得距离进行测量.其中,

在上式中第三项Wi对Ei·Xh和H的相似程度进行加权, 第二项通过约矩阵Ei·H的秩, 来达到约束Ei·Xh的秩的目的.式 (13) 为最终的图像超分辨率的重建模型, 所求得的Xh1即为原始高分辨率图像Xh的一个初步估计图像.

3.2 高频成分恢复
初步重建得到的高分辨率图像在低秩矩阵模型的约束下, 可以保证图像在整体结构上与原始高分辨率图像保持一致, 但是在图像信号的成分上仍缺失一些必要的高频分量.这一节的主要工作, 借鉴Yang提出的一种低分辨图像到高分辨率图像的映射方法恢复初步重建出的高分辨率图像中缺失的高频成分.创新点主要是结合图像低秩矩阵稀疏分解理论提出了一种新的字典训练集构建方法.

3.2.1 字典学习
首先搜集一些高质量的高分辨率图像, 作为字典训练集样本.通过对输入的高分辨率图像样本信号进行低秩矩阵稀疏分解, 根据各部分的结构信息特征将低秩部分作为低分辨率图像块样本集的构建输入, 稀疏部分作为高分辨率样本集的构建输入, 进行联合高低分辨率字典训练.图1所示为字典学习过程.

图1 字典学习过程结构框图

基于相应的高低图像块之间存在着相同的稀疏表示系数, 得phk≈HD·qk, 从而推导出高频主要字典HD, 通过如下优化方法求解得到:

其中矩阵Ph和Q分别有集合phk和qk组成, 这里Q是行满秩的, 则公式 (15) 封闭解为:

这里, 我们得到最终的高低分辨率字典HD和MD.

3.2.2 图像恢复阶段

将第一步重建得到的高分辨率图像的初始估计Xh1分解为相互重叠的图像块, 构成低分辨率图像块集合pkl, 这里我们利用正交匹配追踪算法 (OMP) 在主要低频字典LD下对每一个向量pkl进行稀疏编码, 得到每一个图像块向量的稀疏表示系数集合qk

然后依据phk=HD·qk重构出高分辨率的图像块, 重构模型为

这里RK算子表示从图像位置为K处提取图像块的操作.上述公式的最小二成解为

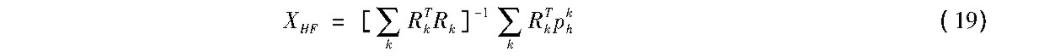
这样我们得到了高分辨率主要高频成分图像XHF, 将其与第一步重建得到的高分辨率图像求和, 得到含有更多高频成分的临时高分辨率图像Xh2.

二、部分源代码

param.L = 3;   % number of elements in each linear combination.
param.K = 50; % number of dictionary elements
param.numIteration = 50; % number of iteration to execute the K-SVD algorithm.

param.errorFlag = 0; % decompose signals until a certain error is reached. do not use fix number of coefficients.
%param.errorGoal = sigma;
param.preserveDCAtom = 0;

%%%%%%% creating the data to train on %%%%%%%%
N = 1500; % number of signals to generate
n = 20;   % dimension of each data
SNRdB = 20; % level of noise to be added
[param.TrueDictionary, D, x] = gererateSyntheticDictionaryAndData(N, param.L, n, param.K, SNRdB);
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%% initial dictionary: Dictionary elements %%%%%%%%
param.InitializationMethod =  'DataElements';

param.displayProgress = 1;
disp('Starting to  train the dictionary');

[Dictionary,output]  = KSVD(D,param);

disp(['The KSVD algorithm retrived ',num2str(output.ratio(end)),' atoms from the original dictionary']);

[Dictionary,output]  = MOD(D,param);

disp(['The MOD algorithm retrived ',num2str(output.ratio(end)),' atoms from the original dic

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.
[5]穆瑞娟,徐胜南,王春兴.基于低秩约束和字典学习的图像超分辨率重建[J].山东师范大学学报(自然科学版). 2016,31(04)