我想问关于主成分分析法的计算中,需要求特征值,特征向量,但是求它们的原因是啥?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了我想问关于主成分分析法的计算中,需要求特征值,特征向量,但是求它们的原因是啥?相关的知识,希望对你有一定的参考价值。
为什么求出特征值和向量就能得到贡献率,它们两个的具体含义是什么?
参考技术A 贡献率反应的是某个因子相对的影响大小,反映的是相关矩阵,它对应的是相关矩阵的特征值:特征值大的,贡献率就大意义:大的特征值表示了相关矩阵中某一成分的方差影响大,这样的因子分析起来才会有效果。
小的特征值则说明相关矩阵中对应部分的方差小,这样,这个因子在不同情况下的变动就小,我们就可以选择不分析这样的因子
因而,可以通过贡献率来得到“主成分”本回答被提问者采纳
一篇弄懂主成分分析及matlab实现
主成分分析及matlab实现
在实际问题研究中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的。因此,人们会很自然地想到,能否在相关分析的基础上,用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息?
事实上,这种想法是可以实现的,主成分分析方法就是综合处理这种问题的一种强有力的工具。主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。从数学角度来看,这是一种降维处理技术。
例如,某人要做一件上衣要测量很多尺寸,如身长、袖长、胸围、腰围、肩宽、肩厚等十几项指标,但某服装厂要生产一批新型服装绝不可能把尺寸的型号分得过多
?而是从多种指标中综合成几个少数的综合指标,做为分类的型号,利用主成分分析将十几项指标综合成3项指标,一项是反映长度的指标,一项是反映胖瘦的指标,一项是反映特体的指标。
一、主成分分析的基本原理
假定有n个样本,每个样本共有p个变量,构成一个n×p阶的数据矩阵
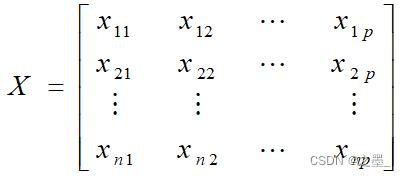
当p较大时,在p维空间中考察问题比较麻烦。为了克服这一困难,就需要进行降维处理,即用较少的几个综合指标代替原来较多的变量指标,而且使这些较少的综合指标既能尽量多地反映原来较多变量指标所反映的信息,同时它们之间又是彼此独立的。
二、定义
记x1,x2,…,xP为原变量指标,z1,z2,…,zm(m≤p)为新变量指标
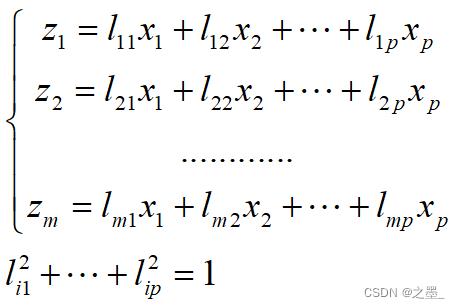
系数lij的确定原则:
① zi与zj(i≠j;i,j=1,2,…,m)相互无关;
② z1是x1,x2,…,xP的一切线性组合中方差最大者,z2是与z1不相关的x1,x2,…,xP的所有线性组合中方差最大者;
zm是与z1,z2,……,zm-1都不相关的x1,x2,…xP, 的所有线性组合中方差最大者。
则新变量指标z1,z2,…,zm分别称为原变量指标x1,x2,…,xP的第1,第2,…,第m主成分。
从以上的分析可以看出,主成分分析的实质就是确定原来变量xj(j=1,2 ,…, p)在诸主成分zi(i=1,2,…,m)上的荷载 lij( i=1,2,…,m; j=1,2 ,…,p)。 从数学上可以证明,它们分别是相关矩阵m个较大的特征值所对应的特征向量。
三、主成分分析的计算步骤
设有 n 个样品,每个样品观测 p 个指标,将原始数据写成矩阵

1. 将原始数据标准化
这里不妨设上边矩阵已标准化了
2. 建立变量的相关系数阵:

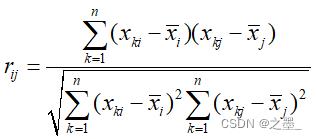
3. 求R的特征根及相应的单位特征向量:


4.写出主成分


5.计算主成分贡献率及累计贡献率

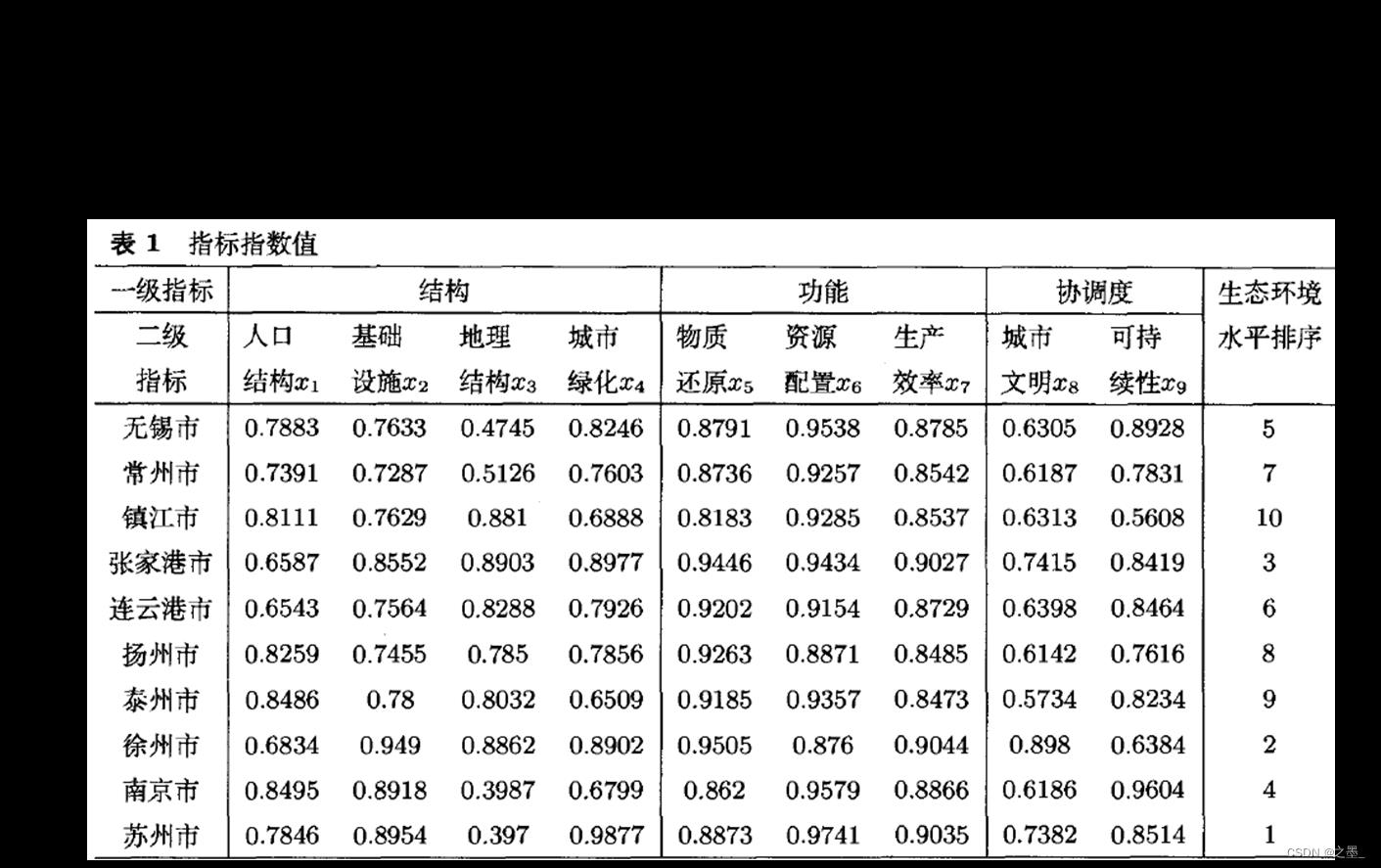
四、 实例









五、主成分分析的应用











以上是关于我想问关于主成分分析法的计算中,需要求特征值,特征向量,但是求它们的原因是啥?的主要内容,如果未能解决你的问题,请参考以下文章
主成分分析法中特征向量有啥意思 ,能用来评估对应变量的权值吗