行列式的计算方法

Posted 2023-05-05

行列式的计算方法如下：

1、逆推法：逆推法主要是建立起来两个行列式之间的一个递推关系式，将整个式子逐步的推下去，从而可以求出来一个具体的值。

2、范德蒙行列式：范德蒙行列式的用法主要是将一些行列式的特点找到变形的一些地方，将我们需要求的一个行列式化成一个已知的或者是简单的形式，而这一种解题方法我们就叫做范德蒙行列式，这也是一种最为常见最为常用到的解题方法。

行列式的性质

1、单位矩阵的行列式为 1 ，与之对应的是单位立方体的体积是 1。

2、行列式的某一行(列)中所有的元素都乘以同一数k，等于用数k乘此行列式。

3、在消元的过程中，行列式不会改变，如果有行交换的话，符号不同。

参考技术A

行列式的计算方法：

1、利用行列式定义直接计算：行列式是由排成n阶方阵形式的n²个数aij确定的一个数，其值为n！项之和。

2、利用行列式的性质计算。

3、化为三角形行列式计算：若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。

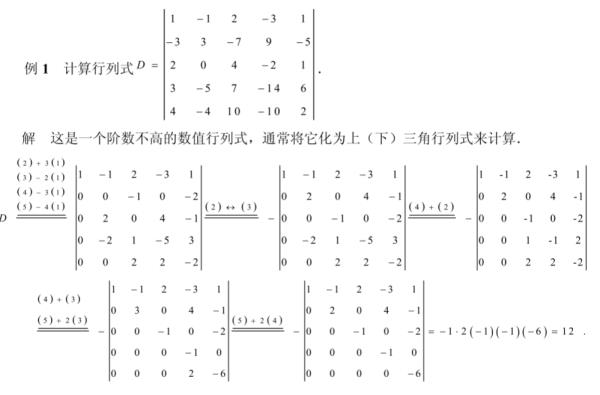
行列式的重要性质：

如果行列式的值为0，则矩阵是奇异矩阵，也就是矩阵没有逆。将某一行的乘以某个数加到另一行上，行列式的值不会变。这一条是我们计算行列式的重要方法，实际上，在很多计算软件中，都是先进行消元过程将矩阵转化为上三角矩阵，然后再进行计算。

计算行列式的最快方法是啥？

【中文标题】计算行列式的最快方法是啥？

【英文标题】：What is the fastest way to calculate determinant?计算行列式的最快方法是什么？

【发布时间】：2016-03-28 00:18:29

【问题描述】：

我正在编写一个库，我想在其中拥有一些没有任何依赖关系的基本 NxN 矩阵功能，这有点像一个学习项目。我正在将我的表现与 Eigen 进行比较。我已经能够与 SSE2 相当，甚至在几个方面都击败了它，而 AVX2 在很多方面都击败了它（它只使用 SSE2，所以并不令人惊讶）。

我的问题是我正在使用高斯消元法创建一个上对角矩阵，然后将对角线相乘以获得行列式。我在 N

可以进行更多优化，但时序看起来更像是算法时序复杂性问题，或者我没有看到主要的 SSE 优势。尝试时，简单地展开循环对我来说并没有多大作用。

有没有更好的计算行列式的算法？

标量代码

/*
    Warning: Creates Temporaries!
*/
template<typename T, int ROW, int COLUMN> MML_INLINE T matrix<T, ROW, COLUMN>::determinant(void) const

    /*
    This method assumes square matrix
    */
    assert(row() == col());
    /*
    We need to create a temporary
    */
    matrix<T, ROW, COLUMN> temp(*this);
    /*We convert the temporary to upper triangular form*/
    uint N = row();
    T det = T(1);
    for (uint c = 0; c < N; ++c)
    
         det = det*temp(c,c);
        for (uint r = c + 1; r < N; ++r)
        
            T ratio = temp(r, c) / temp(c, c);
            for (uint k = c; k < N; k++)
            
                temp(r, k) = temp(r, k) - ratio * temp(c, k);
            
        
    

    return det;

AVX2

template<> float matrix<float>::determinant(void) const

    /*
    This method assumes square matrix
    */
    assert(row() == col());
    /*
    We need to create a temporary
    */
    matrix<float> temp(*this);
    /*We convert the temporary to upper triangular form*/
    float det = 1.0f;

    const uint N = row();
    const uint Nm8 = N - 8;
    const uint Nm4 = N - 4;

    uint c = 0;
    for (; c < Nm8; ++c)
    
        det *= temp(c, c);
        float8 Diagonal = _mm256_set1_ps(temp(c, c));

        for (uint r = c + 1; r < N;++r)
        
            float8 ratio1 = _mm256_div_ps(_mm256_set1_ps(temp(r,c)), Diagonal);

            uint k = c + 1;
            for (; k < Nm8; k += 8)
            
                float8 ref = _mm256_loadu_ps(temp._v + c*N + k);
                float8 r0 = _mm256_loadu_ps(temp._v + r*N + k);

                _mm256_storeu_ps(temp._v + r*N + k, _mm256_fmsub_ps(ratio1, ref, r0));
            

            /*We go Scalar for the last few elements to handle non-multiples of 8*/
            for (; k < N; ++k)
            
                _mm_store_ss(temp._v + index(r, k), _mm_sub_ss(_mm_set_ss(temp(r, k)), _mm_mul_ss(_mm256_castps256_ps128(ratio1),_mm_set_ss(temp(c, k)))));
            
        
    

    for (; c < Nm4; ++c)
    
        det *= temp(c, c);
        float4 Diagonal = _mm_set1_ps(temp(c, c));

        for (uint r = c + 1; r < N; ++r)
        
            float4 ratio = _mm_div_ps(_mm_set1_ps(temp[r*N + c]), Diagonal);
            uint k = c + 1;
            for (; k < Nm4; k += 4)
            
                float4 ref = _mm_loadu_ps(temp._v + c*N + k);
                float4 r0 = _mm_loadu_ps(temp._v + r*N + k);

                _mm_storeu_ps(temp._v + r*N + k, _mm_sub_ps(r0, _mm_mul_ps(ref, ratio)));
            

            float fratio = _mm_cvtss_f32(ratio);
            for (; k < N; ++k)
            
                temp(r, k) = temp(r, k) - fratio*temp(c, k);
            
        
    

    for (; c < N; ++c)
    
        det *= temp(c, c);
        float Diagonal = temp(c, c);
        for (uint r = c + 1; r < N; ++r)
        
            float ratio = temp[r*N + c] / Diagonal;
            for (uint k = c+1; k < N;++k)
            
                temp(r, k) = temp(r, k) - ratio*temp(c, k);
            
        
    

    return det;

【问题讨论】：

鉴于您显然已准备好深入研究细节，并且 Eigen 是开源的...why not look at what it does 或逐步完成...？

他们的方法对我来说没有多大意义，因此很难适应我的图书馆的运作方式。如果我理解它背后的数学推理，我就能很容易地适应它。我认为这与我开始研究的部分旋转有关。其他方法对我来说很有意义，但这是我第一次无法理解其背后的方法。一般来说，只是好奇另一个大脑是否有“最好的方法”的想法。即使在发布了这个问题之后，我仍然非常关注它，当我找到更好的方法时会发布我的代码。

this 你可能会感兴趣。

我认为您需要进行旋转以处理 (0 1; 1 0) 等具有行列式 -1 的矩阵，但我认为您的方法将在该矩阵上失败。

是的，它会的，我正在努力弄清楚我想在这样做之前使用什么算法。

【参考方案1】：

通过高斯消元法将 n × n 矩阵缩减为上（或下）三角形形式的算法通常具有 O(n^3) 的复杂度（其中 ^ 表示“幂”）。

存在计算行列式的替代方法，例如评估特征值集（方阵的行列式等于其特征值的乘积）。对于一般矩阵，完整特征值集的计算也是 - 实际上 - O(n^3)。

然而，理论上，特征值集的计算具有n^w 的复杂性，其中 w 介于 2 和 2.376 之间 - 这意味着对于（很多）更大的矩阵，它比使用高斯消元法更快。查看 James Demmel、Ioana Dumitriu 和 Olga Holtz 在 Numerische Mathematik 中的文章“快速线性代数是稳定的”，第 108 卷，第 1 期，第 59-91 页，2007 年 11 月。如果 Eigen 使用复杂度更低的方法比 O(n^3) 更大的矩阵（我不知道，从来没有理由调查这些事情）可以解释你的观察。

【讨论】：

感谢这篇论文很有趣。我认为“块 LU 分解”是 Eigen 用于 8x8 子块的方法。那篇论文说时间复杂度约为 O(n^2.5)。我也会更多地研究特征值选项。

【参考方案2】：

大多数地方的答案似乎都是使用 Block LU Factorization 在同一内存空间中创建下三角矩阵和上三角矩阵。它是 ~O(n^2.5) 取决于您使用的块的大小。

这是莱斯大学的一个简报，用于解释该算法。

www.caam.rice.edu/~timwar/MA471F03/Lecture24.ppt

除以矩阵意味着乘以它的逆矩阵。

这个想法似乎是显着增加 n^2 操作的数量，但减少 m^3 的数量，这实际上降低了算法的复杂性，因为 m 具有固定的小尺寸。

要花一点时间以一种有效的方式写出来，因为要有效地写出来需要我还没有写过的“就地”算法。