pytorch常用normalization函数

Posted 2023-04-27

参考技术A 将输入的图像shape记为[N, C, H, W]，这几个方法主要的区别就是在，
batchNorm是在batch上，对NHW做归一化，对小batchsize效果不好；
layerNorm在通道方向上，对CHW归一化，主要对RNN作用明显；
instanceNorm在图像像素上，对HW做归一化，用在风格化迁移；
GroupNorm将channel分组，然后再做归一化；
SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

归一化与反归一化
https://blog.csdn.net/rehe_nofish/article/details/111413690

pytorch优雅的反归一化
https://blog.csdn.net/square_zou/article/details/99314197?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control

重点关注

图片保存：torchvision.utils.save_image(img, imgPath)
https://blog.csdn.net/weixin_43723625/article/details/108159190

PyTorch学习（十四）Batch_Normalization（批标准化）

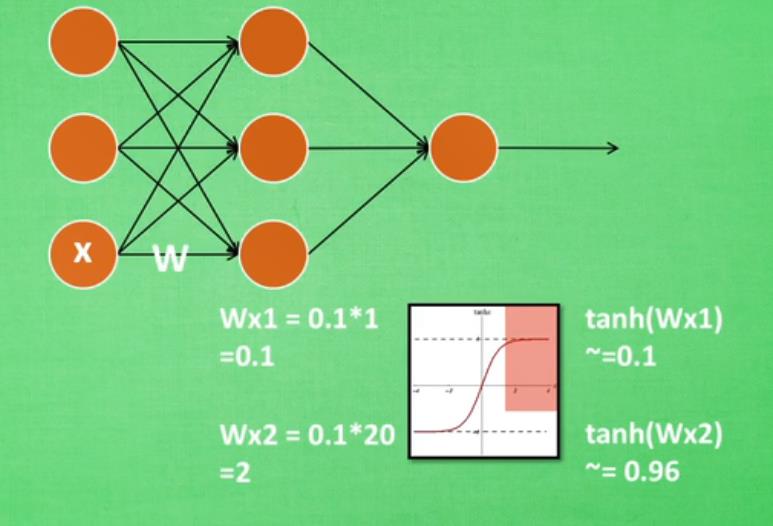
神经网络太深的话，传到后面，受到激励函数饱和区间、失效期间的影响，最后导致神经网络学不到了。

批标准化：将分散数据统一的一种方法，优化神经网络。处理方式大概为下图：

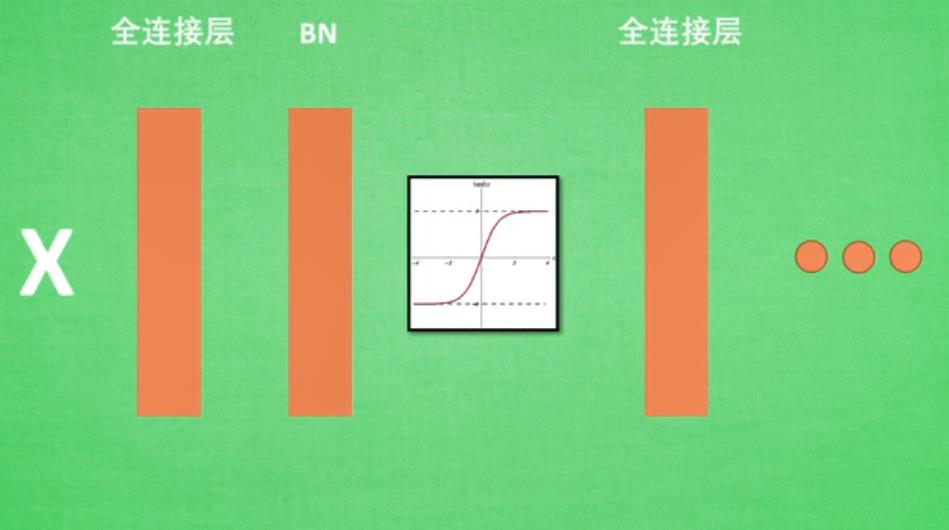
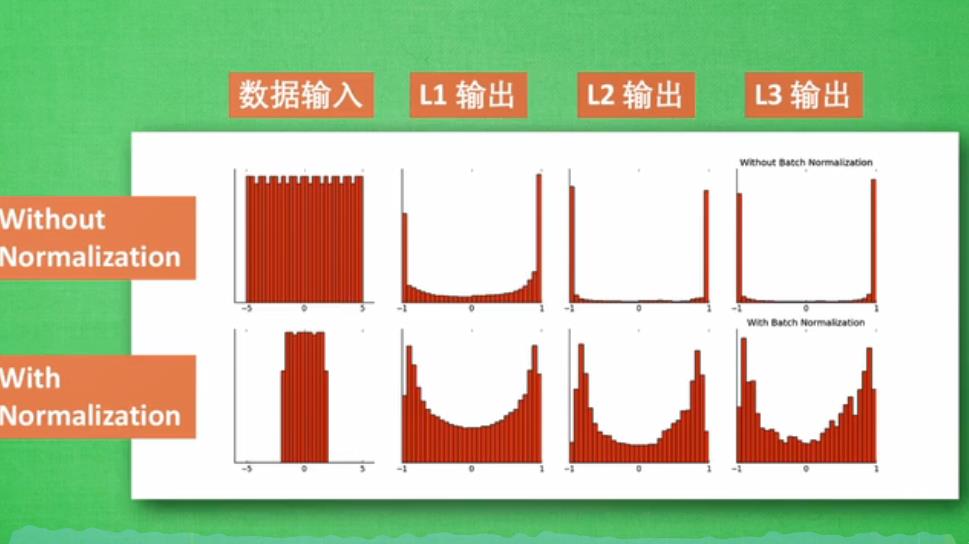
代码如下：

import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np

# torch.manual_seed(1)    # reproducible
# np.random.seed(1)

# 
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8 #8层
ACTIVATION = torch.tanh#采用的激活函数
B_INIT = -0.2   #

# 训练数据
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise

# 测试数据
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise

train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()

train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

# 看一下数据
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')

#搭建网络
class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        self.do_bn = batch_normalization   #批处理
        self.fcs = []#定义两个list
        self.bns = []
        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   #  

        #下面定义hiddenlayer
        for i in range(N_HIDDEN):               # 
            input_size = 1 if i == 0 else 10
            fc = nn.Linear(input_size, 10)
            setattr(self, 'fc%i' % i, fc)       # 
            self._set_init(fc)                  # 
            self.fcs.append(fc)
            if self.do_bn:
                bn = nn.BatchNorm1d(10, momentum=0.5)
                setattr(self, 'bn%i' % i, bn)   # 
                self.bns.append(bn)

        self.predict = nn.Linear(10, 1)         # 
        self._set_init(self.predict)            #  

    def _set_init(self, layer):
        init.normal_(layer.weight, mean=0., std=.1)
        init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        pre_activation = [x]
        if self.do_bn: x = self.bn_input(x)     # input batch normalization
        layer_input = [x]
        for i in range(N_HIDDEN):
            x = self.fcs[i](x)
            pre_activation.append(x)
            if self.do_bn: x = self.bns[i](x)   # batch normalization
            x = ACTIVATION(x)
            layer_input.append(x)
        out = self.predict(x)
        return out, layer_input, pre_activation


#没有和有批处理的神经网络
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]


#创建两个优化函数
opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]

loss_func = torch.nn.MSELoss()


def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
    for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
        [a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
        if i == 0:
            p_range = (-7, 10);the_range = (-7, 10)
        else:
            p_range = (-4, 4);the_range = (-1, 1)
        ax_pa.set_title('L' + str(i))
        ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)
        ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')
        for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())
        ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)
        axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')
    plt.pause(0.01)


if __name__ == "__main__":
    f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))
    plt.ion()  
    plt.show()

    # 训练
    losses = [[], []]  # 

    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        layer_inputs, pre_acts = [], []
        for net, l in zip(nets, losses):
            net.eval()              #  
            pred, layer_input, pre_act = net(test_x)
            l.append(loss_func(pred, test_y).data.item())
            layer_inputs.append(layer_input)
            pre_acts.append(pre_act)
            net.train()             #  
        plot_histogram(*layer_inputs, *pre_acts)     #    

        for step, (b_x, b_y) in enumerate(train_loader):
            for net, opt in zip(nets, opts):     #  
                pred, _, _ = net(b_x)
                loss = loss_func(pred, b_y)
                opt.zero_grad()
                loss.backward()
                opt.step()    #  

    plt.ioff()

    plt.figure(2)
    plt.plot(losses[0], c='#FF9359', lw=3, label='Original')
    plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')
    plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')

    #  
    #  
    [net.eval() for net in nets]    #  
    preds = [net(test_x)[0] for net in nets]
    plt.figure(3)
    plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')
    plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')
    plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
    plt.legend(loc='best')
    plt.show()

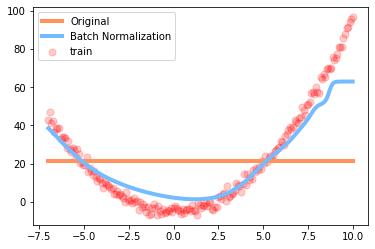
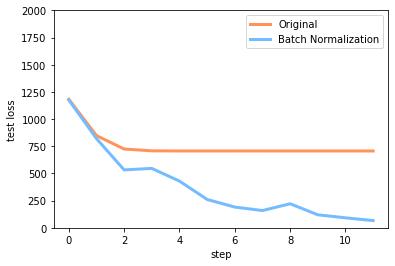
结果图：
学习效果：原来的神经网络死掉了，而批处理的还可以进行学习。

误差变换曲线：原来的误差基本不变了，批处理的还在进行学习，减小误差。