只有方阵才能是满秩矩阵，满秩矩阵存在逆矩阵。也就是 |A|≠0
矮胖矩阵A(m,n),m<n不存在逆矩阵，因为利用Ax=y进行空间映射空间维度被压缩了，也就是说对于目标空间中的y坐标，在原始空间中有多个x与之对应。属于满射。
高瘦矩阵A(m,n),m>n不存在逆矩阵，因为在目标空间中的某个y可能找不到原始空间的某个x与之对应。比如A(3,2)映射后的目标空间是R^3,但是实际上映射的结果是R^3中的一个二维平面。在平面外的目标空间中的任意一点找不到原始空间的x与之对应。

矩阵的秩

列秩：即A的列空间的维度，也就是列向量组的秩，记做rank(col(A))，矩阵的列向量组线性无关则称为列满秩，单射。反之，列向量组线性相关则列不满秩，非单射，非单射则Ax=0有非零解。
不会升维：值域的维度小于等于定义域的维度，也就是不会出现升维的情况。
行秩：行向量组的秩叫做行秩，行向量组线性无关，称为行满秩。行秩=列秩。由m个行向量组成的向量组的秩为m，则行向量组满秩，即行满秩。

单射、满射、双射

单射：每一个y至多有一个x与之对应，对于矩阵函数Ax=y，如果定义域和值域维度相同则为单射。如果变换后值域维度缩小则不是单射。单射等价于列满秩
满射：每一个y至少有一个x与之对应。此时值域与到达域相等。

对于线性函数而言，满射只可能全部是一对一或全部是多对一，不会两者同时在一个映射中存在。满射等价于行满秩。

矩阵A行满秩，则Ax=b为满射，则方程存在解且不唯一。

双射：既是单射又是满射，称为双射，也就是一一映射。双射等价于行满秩+列满秩。既是列满秩又是行满秩（行秩=列秩）的矩阵称为“满秩矩阵”，定义域=值域=到达域。说明方阵才可能是满秩矩阵。

矩阵A若同时满足行满秩和列满秩，则Ax=b为双射，则映射为一一映射，因此方程Ax=b一定有解，且为唯一解。

逆矩阵<----->满秩矩阵（方阵）<----->双射

矩阵Ax的映射法则：是将标准基用A的列向量（c1，c2）来取代。比如如果c1和c2线性无关则维度保持不变为2，如果c1和c2线性相关则维度小于2.所以基向量c1、c2线性无关是单射，线性相关是非单射。
满秩矩阵可以看作是有限个初等矩阵的乘积，一个矩阵经过初等变换，它仍然是同型同秩矩阵。

矩阵列向量线性无关——>列满秩——>值域维度与定义域相同——>单射

矩阵列向量线性相关——>列不满秩——>值域维度降低——>非单射

满射<——>行满秩
非单非满射=行不满秩+列不满秩

线性方程组Ax=b既不是单射函数，也不是满射函数，可能没有解，也可能是多个解。

对矩阵函数而言，满秩矩阵是双射函数。因此，满秩矩阵存在逆矩阵

逆矩阵求法：

1高斯若尔当法

初等行变换法

西尔维斯特不等式：r(AB) ≥ r(A) + r(B) - n
求矩阵的秩的思路：将矩阵变换为阶梯矩阵形式

线性相关与线性无关

要判断一个向量组是否线性相关，归结为判断齐次线性方程组是否有非零解，若方程组有非零解，则线性相关，否则线性无关。

A为m×n矩阵,则A^TA为可逆方阵的充要条件是，A各列线性无关。

矩阵函数的四个重要概念

矩阵的秩和线性方程组的解

总结：

对于m*n的矩阵A的方程Ax=b，rank(A）= rank(B)时有解，且rank（A）=n时有唯一解，当rank(A)<n时有无数个解。

当A中列向量线性无关时，即A列满秩时rank(A)=rank(B)

非齐次矩阵方程Ax=b的解集，其实是齐次矩阵方程Ax=0的解集的平行线..非齐次矩阵方程的解集是Ax=b的特解p加上Ax=0的通解(也就是零空间N(A))
齐次线性方程组的基础解析的秩=n-r，其中r矩阵A的秩，n为方程组的未知数个数。

转置矩阵的性质

列空间、行空间、零空间之间的关系

对于矩阵Ax=y而言，列空间是值域
行空间和零空间都是定义域的子空间
当Ax=0，行空间与零空间正交

r(行空间)+r(零空间)=n，即行空间和零空间一起构成了整个定义域。或者说行空间与零空间的秩关于定义域互补。

线性代数基本定理，也称为秩零定理

行列式

A满秩 <=> |A|≠0

行列式的目的：行列式出现的目的是为了求解线性方程组
逆序数：在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
奇排列与偶排列
逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列

一个排列中任意的两个元素对换，排列改变奇偶性。
三阶行列式的逆序数表示法
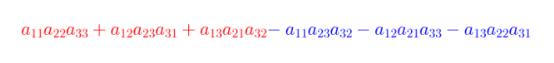
行列式的严格定义
|行列式D|=|行列式D的转置|
只有方阵才有行列式
A不满秩 <=> |A|=0
二阶行列式的三重意义：运算法则、有向面积、线性变换的伸缩比。
交换两行，行列式变号

三维空间的有向面积公式

三阶行列式的有向体积公式

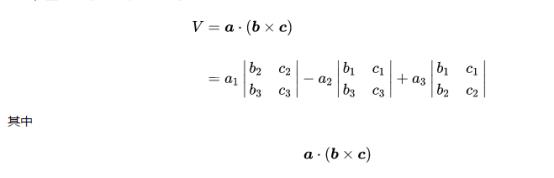
代数余子式

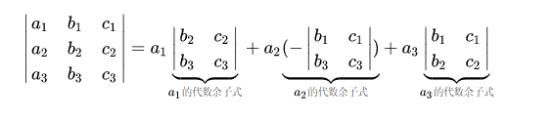
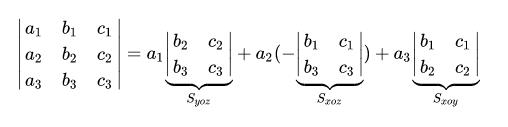
拉普拉斯展开

克莱姆法则--使用行列式解线性方程组

定义：

行列式的解

方阵|A|=0,则列不满秩，行不满秩，非单射，非满射。

方阵|A|≠0，则矩阵A满秩，A可逆，矩阵函数Ax=b为双射（一一映射），方程有唯一解。

方阵|A|≠0<->A满秩<->A可逆，方程Ax=b有唯一解。<->:表示为充要条件

伴随矩阵

A为可逆矩阵，则(A^-1)^* = (A^*)^-1
伴随矩阵的秩

范德蒙行列式

相似矩阵和二次型

基变换：在同一个向量空间中的不同的基下进行坐标变换，就是基变换
完整的基变换图

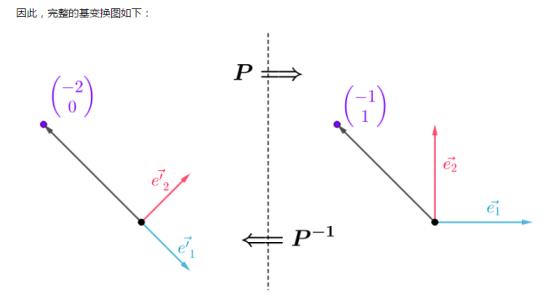
分为正向和反向两种操作，P逆矩阵可以把P所变换的坐标转回去。

过渡矩阵

存在逆矩阵的过渡矩阵是满秩矩阵

等价矩阵的定义

行等价与列等价

列等价：矩阵AQ相当于对A进行了初等列变换，则A~AQ

行等价：矩阵PA相当于对A进行了初等列变换，则A~PA

等价关系的性质

反身性：A~A

对称性：A~B,则B~A

传递性：若A~B,B~C,则A~C

矩阵AB等价的充要条件

相似矩阵

相似矩阵的定义

几何意义

针对指定向量的同一个空间变换，用来在不同基底下进行描述的不同矩阵，彼此之间称之为相似矩阵。

相似矩阵所表示的线性变换，彼此之间称之为相似变换。

表示了矩阵向量在两个不同基底下的相似变换。

相似矩阵的性质

若A和B相似，则A的转置相似B的转置，A的逆相似B的逆，A^k相似B^k
相似矩阵的性质

相似矩阵的用途

把普通的非对角矩阵转换为与其相似的对角矩阵来进行计算处理，简化我们的过程，或者用于提取主要的特征成分等。

矩阵对角化

对角化的定义

其中△是以特征值为主对角线的对角矩阵，P是由特征向量组成的特征矩阵（或者说是过度矩阵）。对角化其实是A相似于△

对角化的条件

n阶矩阵A可以对角化的充要条件是存在n个线性无关的特征向量p1,p2,....pn

特征的含义

在方阵 A 的变换作用下，特征向量 p 的线性变换就是在其向量方向上进行 λλ 倍的伸缩变换。说得更直白一些，就是仅仅只有向量的长度发生改变，但是方向并不改变。具备了这种特殊性，就称之为特征。

一般来说，一个向量在某个矩阵的作用下，其空间变换反映为长度和方向的改变：即旋转、平移和拉伸，有些情况下甚至连维度都会发生变化，而这里的特殊之处就在于，矩阵作用于它的特征向量，仅仅只有长度发生了改变。

特征向量和特征值

线性变换后没有发生方向改变的向量，称为特征向量。

变换前后的伸缩比λ称为特征值。

变换前后的基相同。可表示为：(A-λI)x=0，其中x为非零向量，则(A-λI)是不可逆矩阵。

这个齐次线性方程组有非零解解的条件是：|A-λI|=0，

注意：零向量不是特征向量。同一个特征向量v不能有两个特征值.

A和B相似，则A和B有相同的特征值，有相同的行列式|A|=|B|,有相同的迹，对任意t有tI-A相似tI-B

特征值的相关性质

☆ λ是A的特征值，那么也是A的转置的特征值，而且kλ是kA的特征值，1/λ是A逆的特征值。

特征值λ=0时，如果一个方阵A的某个特征值λ＝0，那么Ap＝0p=0，则意味着该矩阵的零空间就是特征向量p，p是非零向量。该矩阵表示的是空间压缩变换，不可逆，为奇异矩阵。
对角阵diag(1,2,3)表示其特征值分别是1,2,3，对应的特征向量是

如果矩阵 A 的特征向量为 p，特征值为λ，则它的相似矩阵的特征值不变S^-1AS,仍是λ，但是特征向量变为S^-1p。
不同的特征值肯定对应着线性无关的特征向量，但是不能说相同的两个特征值对应的特征向量就一定线性相关，比如我们最熟悉的单位对角矩阵diag(1,1,1)，它的三个特征值都是 1，但是其特征向量分别是:

特征空间的定义

特征值不同---------->特征向量线性无关<---------------------->矩阵A可对角化
特征值相同，要判断特征空间的维度

正交阵的定义

☆ 若A，B是正交阵，则A逆是正交阵，A^n 正交阵，AB也是正交阵。

施密特正交化得到标准正交基

对称矩阵

对称矩阵的定义和性质

定义

一个对称矩阵通过转置操作，得到的仍然是它自身，即满足S=S^T,对称矩阵必须是方阵。

性质：

一个矩阵乘以自己的转置矩,即AA^T，得到的结果必然是一个对称矩阵
对于任意一个实数对称矩阵，都一定可以被对角化。

换句话说，对于一个对称矩阵，无论它的特征值是否重复，它的特征向量都一定线性无关。

实对称矩阵都可以获得一组标准正交的特征向量。
任何一个对称矩阵分解得到的特征向量矩阵都可以是标准正交矩阵Q

由上式，矩阵Q可以表示为

任意一个 n 阶对称矩阵 S，都可以分解成 n 个秩 1 方阵乘以各自权重系数 λi，然后相加的结果。

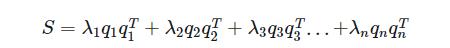
对称矩阵的对角正交化

既对角又正交的矩阵称对角正交矩阵

充要条件：

对称矩阵可以被对角正交化，矩阵可以被对角正交化也说明矩阵是对称矩阵。

正交阵：A转置=A逆

☆ 实对称矩阵特征值互不相同，对应的特征向量相互正交

这里A为对称矩阵A=A^T，P为正交矩阵p^T=P^-1，也就是说对称矩阵A，一定存在正交矩阵P满足以上对角化公式。

二次型矩阵的性质

矩阵合同

二次型的基变换---合同矩阵

对称矩阵的合同矩阵也是对称矩阵
合同矩阵的秩相同

标准型与规范型

标准型：二次型只有二次项，就是二次型的标准型。

二次型的标准型化法

正交变换法

用正交变换化二次型成标准形，具有保持几何形状不变的优点

拉格朗日配方法

若二次型含有xi的平方项，则先把含有xi的乘积项集中，然后配方，再对其余的变量同样进行，直到都配成平方项为止。

正定矩阵

如果一个矩阵的所有特征值都为正，我们称它是“正定的”，如果均为非负（即，最小特征值为 0），相当于结论稍稍弱了一些，我们称之为“半正定的”，如果它含有负的特征值，那么它是非正定的。

那么换句话说，对于一个对称矩阵而言，从特征值的正负性角度来看的话，它一定是正定、半正定或非正定的其中一种。

对称矩阵 A^TA的所有特征值都是非负的，特别的，如果矩阵 A 的列向量线性无关，则该矩阵是正定矩阵，特征值均为正。

A^TA和 AA^T 拥有完全一样的非零特征值。

向量空间补充

矩阵A(m,n)作用下的向量映射

映射后的向量维数和原始向量维数的关系取决于 m 和 n 的关系

如果 m>n，那么目标向量的维数就大于原始向量的维数.

如果 m<n，那么目标向量的维数就小于原始向量的维数。

空间映射

☆ 矩阵A（m，n）存在映射就意味着映射后的点可以被唯一还原。

矮胖矩阵：

m<n即矩阵行数<列数,进行Ax=y映射后，x空间压缩（降维）为y，矩阵A无逆映射

高瘦矩阵：

m>n，即矩阵行数大于列数，进行Ax=y映射后，x空间上升（升维）为y，比如二维向量x经过高瘦A映射后变为三维向量空间y的一个切面（真实是二维），在切面外的点无法被唯一还原为原空间的坐标。矩阵A无可逆映射。

方块矩阵：

m=n，即矩阵行数等于列数，方阵。

当矩阵A的三个列向量线性无关的时候，矩阵A有逆映射，空间没有被压缩，也没有升维。

当矩阵A的三个列向量线性相关的时候，相当于高瘦矩阵的情况。

空间映射形态的决定因素：矩阵A的秩，确切的说是矩阵A线性无关的列向量的个数。

零空间：

记做N(A),满足Ax=0的x的集合。N(A)零空间矩阵A可逆的条件是对应的点是原空间的一个点，比如(0,0,0).

列空间：

矩阵A的每一列组成的空间，记做C(A)，对于矩阵函数Ax=y而言，列空间是值域。

逆映射前提是方阵，但并非每个方阵都可逆，逆矩阵存在的条件是方阵A的各个列向量线性无关。

奇异矩阵：不可逆矩阵就叫奇异矩阵。

向量空间及其子空间

定义

R^n向量空间：R^n必须包含所有的n维向量

向量空间的定义：针对一个向量集合V，若任取V中的两个向量u和v，只要满足u+v仍然V中，同时任取标量c，只要满足cu仍然在V中，则V就构成一个向量空间

子空间：若一个向量空间U的子集V也是一个向量空间，那么V是U的子空间。

R^3空间的子空间：① R^3空间自身 ② R^3空间中过原点的平面或直线 ③ 零向量自身

一个向量的任意子空间都包含零向量

注意区别目标空间和映射后向量的构成空间之间的区别

矩阵A(m,n)的四个重要的子空间

①列空间

由A的列向量张成的空间。包含了n个m维的列向量的线性组合，记做C(A),它是R^m空间的子空间，对于一个线性方程组Ax=b，只有当向量b可以写成矩阵A的各列的线性组合，值域一定在列空间中。x1a1+x2a2+.....+xnan的方式,方程组才有解，换句话说，当且仅当b在矩阵A的列空间中时，方程才有解。

② 零空间：

所有满足 Ax=0 的向量 x 的集合就称之为矩阵 A 的零空间。

如果矩阵 A 的各列线性无关，则 x 就只有零向量这个唯一解.

如果 A 的各列线性相关，那么 x 就有非零解

零空间满足向量空间的定义，因此也是一个向量空间。

对于m×n矩阵A而言，零空间里的向量是n维的，是R^n的子空间

③ 行空间：

对于m×n矩阵A而言，矩阵各行向量所张成的空间，其实是A^T的列空间，记做C(A^T),因为行向量有n个成分，所以其行空间为R^n的子空间。

④ 左零空间

矩阵线性代数笔记整理汇总，超全面

javascript的笔记精简版

纯手工修复fstab文件以及boot目录(Centos6.8)

机器学习笔记线性回归

李宏毅线性代数笔记6：矩阵的计算

数据分析学习汇总