《搜索和推荐中的深度匹配》——2.2 搜索和推荐中的匹配模型

Posted 2022-12-10 小爷毛毛（卓寿杰）

接下来，我们概述搜索和推荐中的匹配模型，并介绍潜在空间中的匹配方法。

2.2.1 搜索中的匹配模型

当应用于搜索时，匹配学习可以描述如下。一组查询文档对$D=（q_1，d_1，r_1），（q_2，d_2，r_2），...，（q_N，d_N，r_N）$作为训练数据给出，其中$q_i，d_i和r_i（i=1，...，N）$分别表示查询，文档和查询文档匹配度（相关性）。每个元组$（q，d，r）\in D$的生成方式如下：查询q根据概率分布$P（q）$生成，文档d根据条件概率分布$P（d|q）$生成，并且相关性r是根据条件概率分布$P（r|q，d）$生成的。这符合以下事实：将query独立提交给搜索系统，使用query words检索与query关联的文档，并且文档与query的相关性由query和文档的内容确定。带有人类标签的数据或点击数据可以用作训练数据。

匹配学习以进行搜索的目的是自动学习一个表示为得分函数$f（q，d）$（或条件概率分布$P（r|q，d）$）的匹配模型。可以将学习问题形式化为公式（2.1）中的 pointwise loss function，公式（2.2）中的 pairwise loss function 或公式（2.3）中的 listwise loss function 的最小化。学习的模型必须具有泛化能力，可以对看不见的测试数据进行匹配。

2.2.2 推荐中的匹配模型

当应用于推荐时，匹配学习可以描述如下。给出了一组M个用户$U=u_1，...，u_M$和一组N个项目$V=i_1，...，i_N$，以及评级矩阵$R\in R^{M\times N}$，其中每个条目$r_{ij}$表示用户$u_i$在项目$i_j$上的评分（互动），如果该评分（互动）未知，则$r_{ij}$设置为零。我们假定每个元组$（u_i，i_j，r_{ij}）$的生成方式如下：用户$u_i$是根据概率分布$P（u_i）$生成的，项目$i_j$是根据概率分布$P（i_j）$生成的，根据条件概率分布$P（r_{ij}|u_i，i_j）$生成评级$r_{ij}$。这对应于以下事实：在推荐系统中显示了用户和项目，而用户对项目的兴趣由系统中用户对项目的已知兴趣确定。

匹配学习推荐的目的是学习基础匹配模型$f（u_i，i_j）$，该模型可以对矩阵R中零项的评分（相互作用）做出预测：

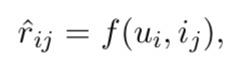
其中${\hat{r}}_{ij}$表示用户$u_i$和项目$i_j$之间的估计得分，以此方式，给定用户，可以推荐相对于该用户具有最高分数的项目的子集。学习问题可以形式化为最小化正则经验损失函数。仍然，损失函数可以是pointwise loss、pairwise loss 或 listwise loss，如公式（2.1），公式（2.2）或公式（2.3）所示。如果损失函数是像平方损失或交叉熵之类的pointwise loss，则模型学习将成为回归或分类问题，其中预测值表示感兴趣的强度。如果损失函数为成pairwise loss 或 listwise loss，则成为排序问题，其中预测值指示用户对商品的兴趣的相对强度。

2.2.3 潜在空间中匹配

如第1节所述，在搜索和推荐中进行匹配的基本挑战是来自两个不同空间（查询和文档以及用户和项目）的对象之间的不匹配。解决挑战的一种有效方法是在一个公共空间中匹配表示两个对象，并在公共空间中执行匹配任务。由于空间可能没有明确的定义，因此通常称为“潜在空间”。这是潜在空间中匹配方法【1】【2】背后的基本思想。

在不失一般性的前提下，让我们以搜索为例。图2.2说明了潜在空间中的query-文档匹配。

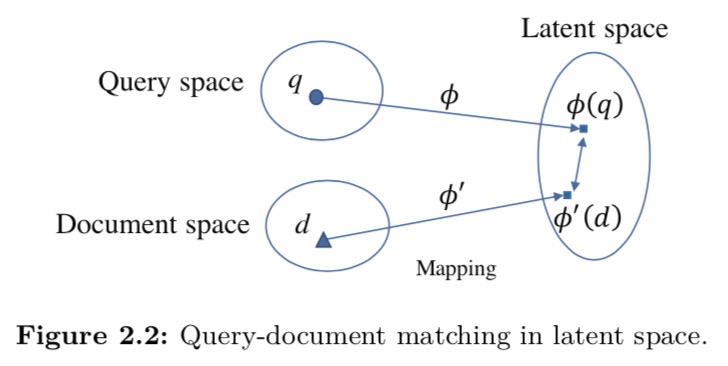
存在三个空间：query空间，文档空间和潜在空间，并且query空间和文档空间之间存在语义间隙。query和文档首先映射到潜在空间，然后在潜在空间中进行匹配。两个映射函数指定从query空间和文档空间到潜在空间的映射。在潜在空间中使用不同类型的映射函数（例如，线性和非线性）和相似性度量（例如，内积和欧几里得距离）会导致不同类型的匹配模型。

形式上，令Q表示query空间（query q∈Q），而D表示文档空间（文档d∈D），而H表示潜在空间。从Q到H的映射函数表示为φ：Q→H，其中φ（q）代表H中q的映射向量。类似地，从D到H的映射函数表示为φ’：D→H，其中φ’（d）代表H中d的映射向量。q和d之间的匹配分数定义为映射向量之间的相似性潜在空间中q和d的（表示），即φ（q）和φ’（d）。

在深度学习盛行之前，大多数方法都是“浅”的，因为分别采用线性函数和内积作为映射函数和相似性。

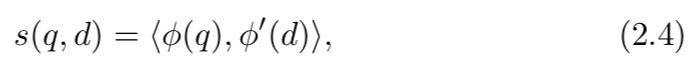
其中φ和φ’表示线性函数，⟨·⟩表示内积。

在学习模型时，给出了query查询和文档之间的匹配关系的训练实例。例如，点击数据可以自然使用。训练数据表示为$（q_1，d_1，c_1），（q_2，d_2，c_2），...，（q_N，d_N，c_N）$，其中每个实例是一个三元组query，文档和点击数（或点击数的对数）。

引文

【1】Wu, W., Z. Lu, and H. Li (2013b). “Learning bilinear model for matching
queries and documents”. Journal of Machine Learning Research. 14(1): 2519–2548. url: http://dl.acm.org/citation.cfm?id=2567709. 2567742.
【2】Koren, Y., R. Bell, and C. Volinsky (2009). “Matrix factorization tech- niques for recommender systems”. Computer. 42(8): 30–37.