《搜索和推荐中的深度匹配》——经典匹配模型 2.1 学习匹配

Posted 2021-05-21 卓寿杰_SoulJoy

2. 经典匹配模型

已经提出了使用传统的机器学习技术进行搜索中的查询文档匹配和推荐中的用户项目匹配的方法。这些方法可以在一个更通用的框架内形式化，我们称之为“学习匹配”。除了搜索和推荐外，它还适用于其他应用，例如释义，问题解答和自然语言对话。本节首先给出学习匹配的正式定义。然后，它介绍了传统学习以匹配为搜索和推荐而开发的方法。最后，它提供了该方向的进一步阅读。

2.1 学习匹配

2.1.1 匹配函数

匹配问题的学习可以定义如下。假设存在两个空间X和Y。在两个空间$x\in X$和$y\in Y$的两个对象上定义了一个匹配函数$F=f（x，y）$，其中每个函数$f：X\times Y\to R$表示两个对象x和y之间的匹配程度。两个对象x和y及其关系可以用一组特征$\Phi （x，y）$来描述。

匹配函数f（x，y）可以是特征的线性组合：

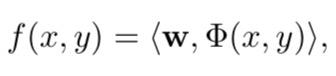
其中w是参数向量。它也可以是广义线性模型，树模型或神经网络。

2.1.2 学习匹配函数

可以采用监督学习来学习匹配函数f的参数，如图2.1所示。

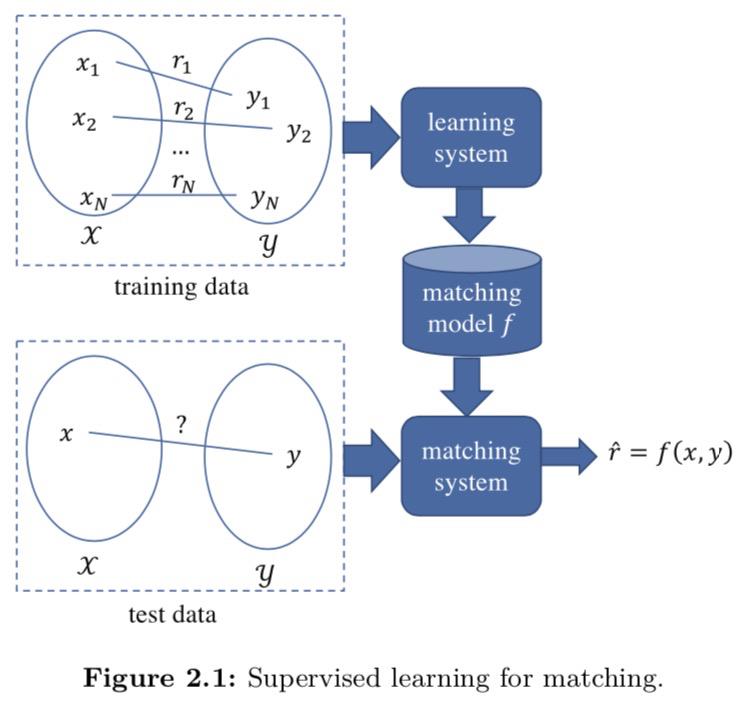
监督学习的匹配通常包括两个阶段：离线学习和在线匹配。在离线学习中，给出了一组训练实例 D = { （ x 1 ， y 1 ， r 1 ） ， . . . ， （ x N ， y N ， r N ） } D = \\{ （x_1，y_1，r_1），...，（x_N，y_N，r_N）\\} D={（x1​，y1​，r1​），...，（xN​，yN​，rN​）}，其中$r_i$是指示对象之间匹配程度的布尔值或实数$x_i$和$y_i$，N是训练数据的大小。进行学习以选择可以在匹配中表现最好的匹配函数f∈F。在在线匹配中，给定一个测试实例（一对对象）$（x，y）\in X\times Y$，学习到的匹配函数f用来预测对象对之间的匹配度，表示为$f（x，y）$。

与其他监督学习问题类似，我们可以将学习匹配的目标定义为最小化损失函数，该函数表示匹配函数在训练数据和测试数据上可以达到多少精度。更具体地，给定训练数据D，学习等于解决以下问题：

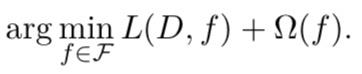
目标由两部分组成：经验损失$L（D，f）$衡量匹配函数f对训练数据产生的总损失，而正则化器$\Omega （f）$防止过拟合训练数据。通常选择$\Omega （f）$来惩罚f的复杂度。流行的正则化器包括l1，l2以及它们的混合。

经验损失函数$L（D，f）$的不同定义导致不同类型的学习以匹配算法。文献中已广泛使用三种类型的损失函数，分别称为点向损失函数(pointwise loss function)，成对损失函数(pairwise loss function)和列表损失函数(listwise loss function)【1】。接下来，我们简要描述三种类型的损失函数。

Pointwise Loss Function

Pointwise Loss Function 仅在一个实例（即源对象和目标对象）上定义。假设存在一对真正匹配度为r的对象$（x，y）$。此外，假设由匹配模型给出的$（x，y）$的预测匹配度是$f（x，y）$。逐点损失函数定义为表示匹配度之间差异的度量，表示为$l^{point}（r，f（x，y））$。$ f（x，y）$与r越近，损失函数的值越小。

在学习中，给定训练数据集 D = { （ x 1 ， y 1 ， r 1 ） ， . . . ， （ x N ， y N ， r N ） } D = \\{（x_1，y_1，r_1），... ，（x_N，y_N，r_N）\\} D={（x1​，y1​，r1​），...，（xN​，yN​，rN​）}，我们将训练数据的总损失或对象对损失的总和最小化：

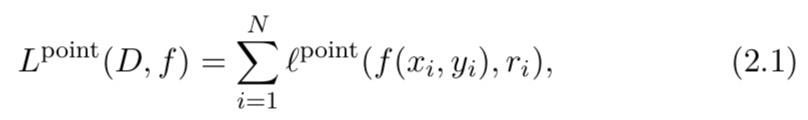
其中$r_i$是训练实例$（x_i，y_i）$的真实匹配度。

作为 Pointwise Loss Function 的一个示例，均方误差（MSE）是广泛使用的损失函数。给定一个带标签的实例$（x，y，r）$和匹配模型f，MSE定义为：

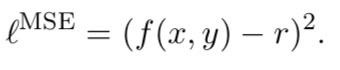
另一个例子是交叉熵损失函数。交叉熵损失函数假设$r\in 0,1$，其中1表示相关，否则为0。进一步假设$f（x，y）\in [0,1]$是x和y相关的预测概率。然后，交叉熵损失定义为：

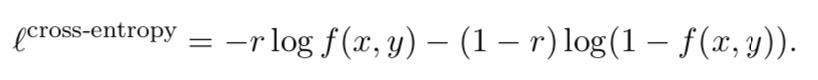
Pairwise Loss Function

假设有两对对象$（x，y^{+}）$和$（x，y^{-}）$，其中一个对象x是共享的。我们称x源对象（例如查询或用户）、$y^{+}$和$y^{-}$为目标对象（例如文档或项目）。进一步假设在给定对象x的情况下，在对象$y^{+}$和$y^{-}$之间存在顺序，表示为$r^{+}>r^{-}$。在此，$r^{+}$和$r^{-}$分别表示$（x，y^{+}）$和$（x，y^{-}）$的匹配度。对象之间的顺序关系可以显式或隐式获得。

引文

【1】Cao, Y., J. Xu, T.-Y. Liu, H. Li, Y. Huang, and H.-W. Hon (2006). “Adapting ranking SVM to document retrieval”. In: Proceedings of the 29th Annual International ACM SIGIR Conference on Re- search and Development in Information Retrieval. SIGIR ’06. Seattle, Washington, DC, USA: ACM. 186–193.
【2】He, X., L. Liao, H. Zhang, L. Nie, X. Hu, and T.-S. Chua (2017c). “Neural collaborative filtering”. In: Proceedings of the 26th Interna- tional Conference on World Wide Web. WWW ’17. Perth, Australia.
173–182.
【3】Joachims, T. (2002). “Optimizing search engines using clickthrough
data”. In: Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’02.
Edmonton, Alberta, Canada: ACM. 133–142.
【4】Nallapati, R. (2004). “Discriminative models for information retrieval”.
In: Proceedings of the 27th Annual International ACM SIGIR Con- ference on Research and Development in Information Retrieval. SIGIR ’04. Sheffield, UK: ACM. 64–71.
【5】Rendle, S., C. Freudenthaler, Z. Gantner, and L. Schmidt-Thieme
(2009). “BPR: Bayesian personalized ranking from implicit feedback”. In: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence. UAI ’09. Montreal, Quebec, Canada: AUAI Press. 452–461. url: http://dl.acm.org/citation.cfm?id=1795114.1 795167.