数据的正态性检验

Posted 2023-04-18

参考技术A 对于我们得到的一组数据，我们日常生活中遇到最多的，应用范围最广的就是正态分布。如果要确定数据是否为正态分布，就要进行正态性检验。检验数据分布常用的检验方法有χ²检验，偏度-峰度检验以及夏皮罗-威尔克法较为有效。

随机变量X的偏度和峰度是指的是X的标准化变量[X-E(X)]/D(X)½的三阶矩和四阶矩。
（PS：关于数据的描述：随机变量的0阶矩为总概率1，1阶矩为数据的期望，2阶矩为表示方差，3阶矩表示偏度，4阶矩表示峰度）
设X1，X2，.....,Xn是来自总体X的样本，则v1,v2的矩估计量分别是，若总体X为正态变量，则可证明当n充分大时，近似的有

相关正态性检验方法有K-S检验，明日再补充

相关软件包在python scipy.stats.kstest中
KS检验是基于样本累积分布函数来进行判断的。可以用于判断某个样本集是否符合某个已知分布，也可以用于检验两个样本之间的显著性差异。KS检验是基于累积分布函数的，如果要进行分布检验，以正态分布为例，首先会画出典型正态分布的累积分布图。然后绘制出数据的累积分布图，通过比较二者最大差值是否大于边界值来判断边界值和D的关系， 如果D小于边界值，则可以认为样本的分布符合已知分布，否则不可以。

除KS检验方法外，还有AD检验和W检验可以用来检测数据的分布特性：

如何判断数据是否符合正态分布？
常见正态性检验方法总结

R语言-数据的正态性检验

关注我

不迷路

R语言-数据的正态性检验

R语言-数据的正态性检验

     数据的分布形势是进行统计学处理的基础，在没有掌握数据结构的情况下进行统计学分析，极有可能得出不可靠的结论，因此对于数据分布的检验就显得非常重要。正态分布是几种常见的数据分布形势，在体育学研究中也较为常见，使用R语言进行数据的正态性的检验非常简单。欲知详情，请点赞关注！

1

01

数据

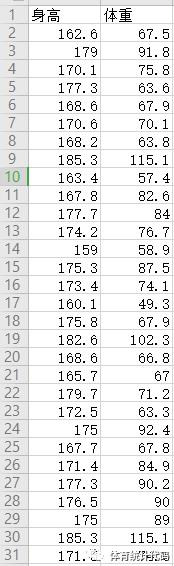
数据如下，这是一份根据真实数据改编的改编数据。

02

读入数据到RStudio

1

方式一

     给出文件的相对路径，首先设置R-Studio的工作目录，然后打开数据文件。设置工作目录为“数据”文件夹。

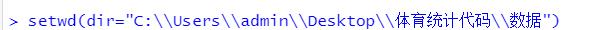
>setwd(dir="C:\Users\admin\Desktop\正在处理\体育统计代码\数据")

读取数据，将数据存放在df数据框里

> read.csv("正态性检验数据.csv",header=T)

2

方式二

     给出文件的绝对路径，无需设置工作目录。

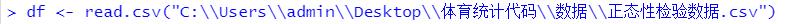
df<-read.csv("C:\Users\admin\Desktop\正在处理\体育统计代码\数据\正态性检验数据.csv",header=T)

3

查看数据

03

绘制条形图

1

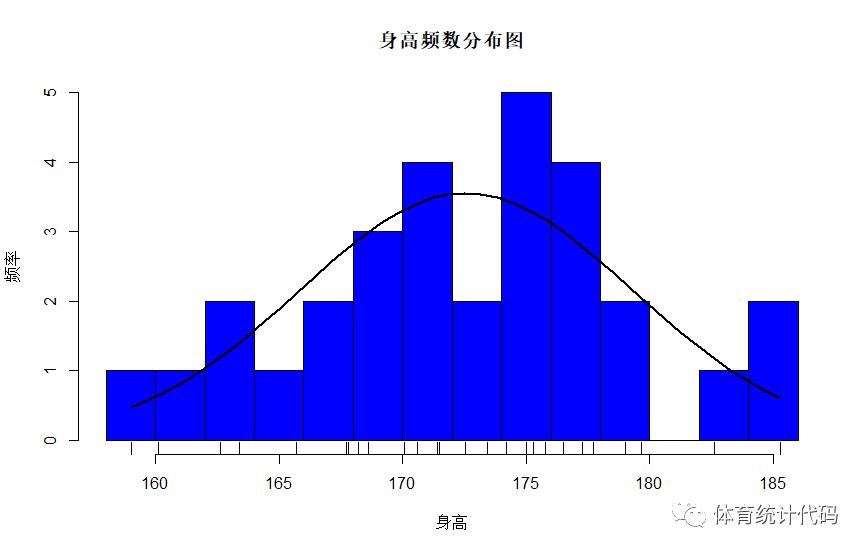
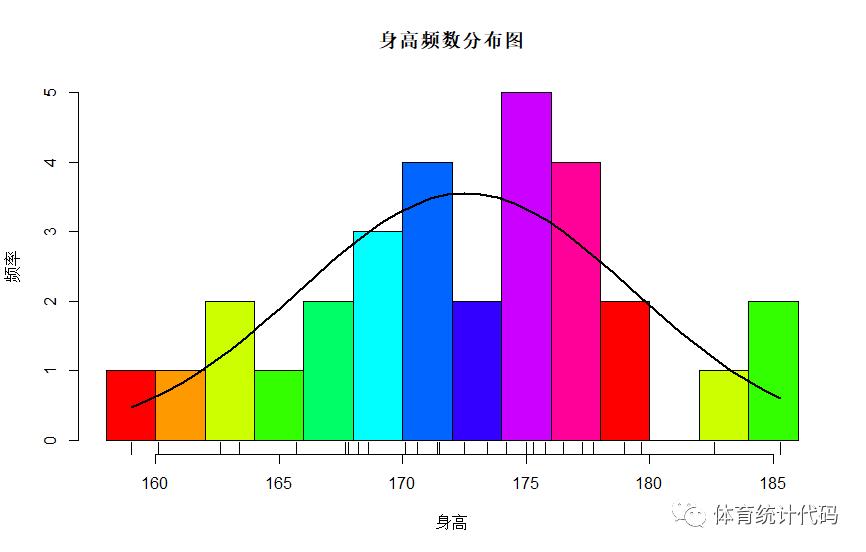
绘制彩色条形图

> h <- hist(df$身高,breaks = 12,col=rainbow(10),xlab="身高",ylab="频率",main = "身高频数分布图")

> x <- df$身高

> xfit <- seq(min(x),max(x),length=40)

> yfit <- dnorm(xfit,mean = mean(x),sd = sd(x))

> yfit <- yfit*diff(h$mids[1:2])*length(x)

> lines(xfit,yfit,col="black",lwd=2)

> rug(jitter(df$身高))#添加轴虚图

> shapiro.test(df$身高)

04

正态性检验

     Shapiro-Wilk (SW) 检验，用于验证一个随机样本数据是否来自正态分布。

1

结果解读

H0：该样本数据服从正态分布。

H1：该样本数据不服从正太分布。

SW检验结果为：p＞0.05，因此接受原假设，认为该样本符合正态分布。

04

参考资料

[1]https://blog.csdn.net/zzminer/article/details/8858469