滞后环节对系统的影响

Posted 2023-04-17

滞后环节是指系统的输出响应相对于输入信号存在一定的延迟或滞后。滞后环节通常由惯性元件或传输延迟等因素引起，会对系统的性能和稳定性产生一定的影响。

下面列举几种滞后环节对系统的影响：

1. 影响系统的稳定性。滞后环节会导致系统的动态特性变慢、惯性增大，降低了系统对外界干扰的适应能力，从而可能导致系统不稳定。

2. 影响系统的精度。滞后环节会使系统输出与实际输出存在一定的误差，从而影响系统的控制精度。

3. 影响系统的响应速度。滞后环节会减缓系统的响应速度，降低系统的快速响应能力，导致系统动态响应时间变长。

4. 增加系统的复杂度。为了克服滞后环节的影响，需要在系统中增加调节器件、滤波器、预测控制器等额外的环节，增加了系统的复杂度。

综上所述，滞后环节对系统的影响主要表现为降低系统的稳定性、控制精度和响应速度，增加系统复杂度。针对不同的系统，需要根据具体情况进行分析和优化设计。 参考技术A 滞后环节对系统的影响一般有以下几点：

1. 延迟响应：由于滞后环节的存在，系统输出的响应会有一定的延迟，导致系统的动态响应变慢。

2. 减小增益：滞后环节的存在会导致系统的增益减小，即使在没有滞后环节的情况下，系统的增益也会比较大，但是加上滞后环节后系统的增益会降低。

3. 稳态误差：滞后环节会引起系统稳态误差，使系统输出无法完全达到期望值。

4. 相位滞后：滞后环节会导致系统输出相位滞后，使系统的相位变得不稳定，影响系统的稳定性和控制性能。

因此，滞后环节对系统的影响是比较明显的，需要在系统设计和控制中进行合理的考虑和处理。 参考技术B 滞后环节会对系统的性能产生负面影响，因为它会延迟系统的响应，使系统变得缓慢。滞后环节还会使系统失去准确性，因为它会影响系统的输出，而这可能会造成潜在的风险。此外，滞后环节还可能影响系统的可靠性，因为它可能会导致系统出现问题，从而影响系统的可用性。 参考技术C 滞后环节对系统的影响是因为有误差的时候，控制器的输出在纯滞后的影响下，会比较晚的作用到被控量上，而同时检测变送测得的数值仍没改变，控制器继续增大输出，超调量会增加，系统就不稳定咯。

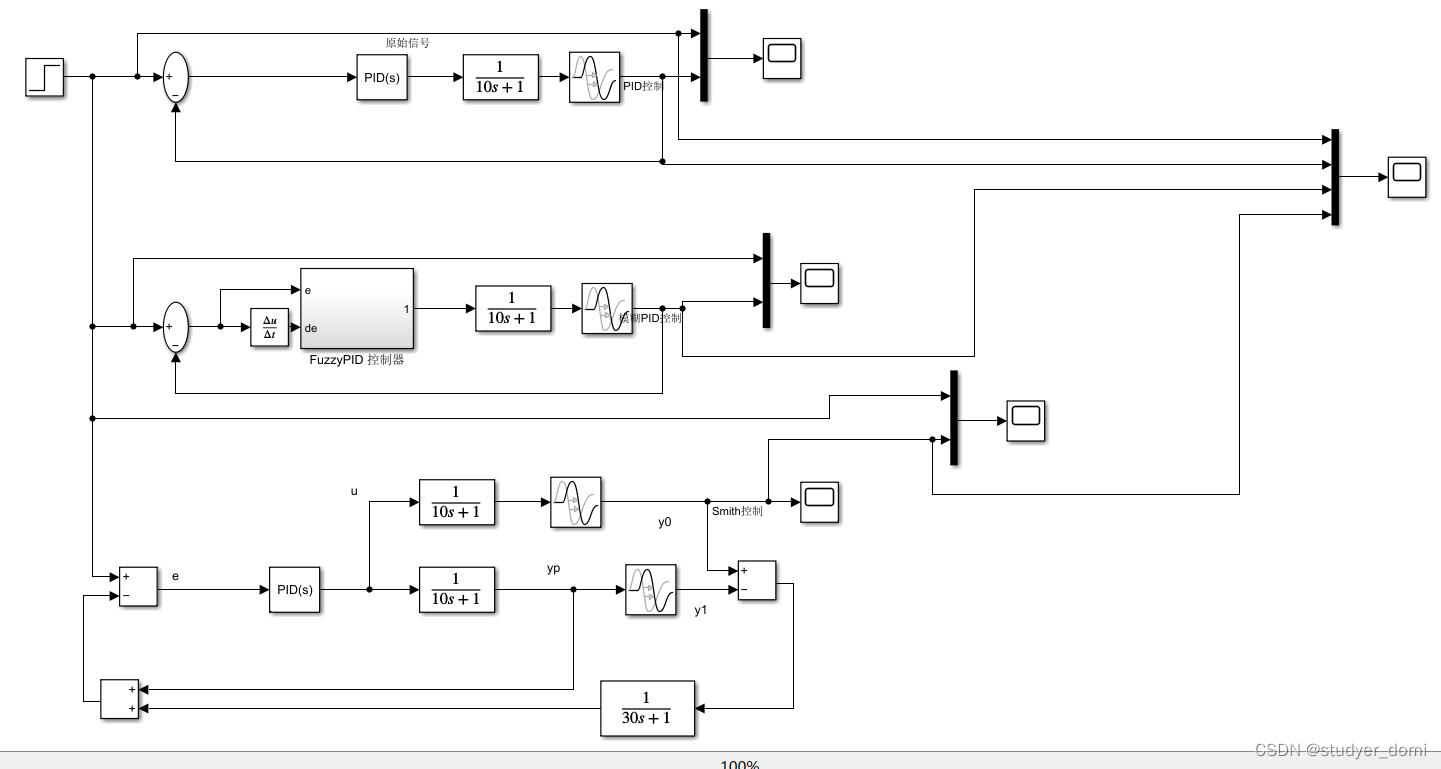
matlab simulink 温度控制时延系统 模糊pid和smith控制

1、内容简介

略
494-可以交流、咨询、答疑

2、内容说明

3 SMITH控制

3.1 SMITH预测原理

 在控制系统中，纯滞后的环节可以出现在不同的位置，它们对过程调节的影响是不同的。以纯滞后单回路控制系统为例，说明了如何减少纯滞后对系统的影响。其结构图如下:

   R(s) Y(s)

           -     -  

图3.1纯滞后补偿的结构图

Gc(s)为普通调节器的传递函数，G(s) exp(-s)为对象的传递函数。则在没有滞后补偿的控制系统的传递函数为:      

                                (3-1)

在闭环传递函数的分母中，还有纯滞后环节exp(一二)，这将导致稳定的减少，当足够大的时候，系统将是不稳定的。为了使系统得到充分补偿，应该有:  

                                    (3-2)

经过完全补偿后，完全补偿后的闭环传递函数为:

                                   (3-3)

它消除了纯滞后部分对控制系统的影响，因为公式中的exp(-s)在闭环控制回路之外，不影响系统的稳定性，拉普拉斯变换定理表明，exp(-s)仅仅为控制作用在时间坐标上推移了一个时间z，而控制系统的过渡过程及其他性能指标都与对象特性为G(s)时完全相同。此种补偿为SMITH预估补偿。

3.2 SMITH预估补偿结构的改进

由于被控对象的参数是会改变的，纯滞后环节通常会用近似式表达式表示，使得出现了预估补偿器不能实现完全补偿，系统的稳定性会变差，为了提高系统的稳定性，将滤波器加入到SMITH预估值和实际系统的输出值的误差回路中，以此增加系统的稳定性。其结构图如下:

图3.2改进的SMITH预估补偿

在这里，GF (s)取为加权平均滤波器，此滤波器的特征:

方法:数据在不同的时间加以不同的权，通常越接近现时刻的数据，权值取得越大。新的采样值权系数越大，灵敏度越高，但信号平滑度越低。

优点:适用于较大纯滞后时间常数的对象和较短的采样周期的系统。

缺点:对于纯滞后时间常数较小，采样周期较长，变化缓慢的信号不能迅速反应系统当前所受干扰的严重程度，滤波效果差。

    由于中央空调的湿度控制通常是存在大滞后，滞后时间长，采样周期不长，故此滤波器适用。

3、仿真分析

略

4、参考论文

略