（高分）用Matlab模拟ASK系统（数字信号处理实验）

Posted 2023-05-04

一、 目的
通过本课程设计使学生深入理解和掌握ASK通讯系统的各个关键环节，包括基带信号形成、调试、解调、滤波、传输、噪声对通信质量的影响等。在数字信号处理实验课的基础上更加深入地掌握数字滤波器的设计原理及实现方法。使学生对ASK系统各个关键点的信号波形及频谱有深刻的认识。
二、 设计内容
本次设计的主要内容是用软件模拟ASK系统。
基带信号采用双极性二元码。基带信号经过低通滤波后再与载波相乘进行调制，经过调制后的信号送入信道传输，在传输过程中，有用信号会受到各种信道噪声影响，我们用白噪声模拟信道噪声。在接收端先经过通带滤波器提取信号，再采用相干解调和抽样判决恢复基带信号。
三、 设计要求

1、 基带信号由本人学号的最低四位生成，每位学号用4位二进制表示，共16位。如学号为98042099，最低四位为2099，其相应的基带信号为：0010000010011001，用双极性二元码表示为：
－1－11－1－1－1－1－11－1－111－1－11。基带信号的码元宽度T＝1/200s，载波频率fc为1000hz。
2、 BPF及LPF均采用有限长滤波器，用频率采样法或窗函数法设计，滤波器的阶数可选63、64、127、128。LPF及BPF的特性如下图：

3、 滤波在时域中用卷积实现。
4、 用C语言或matlab语言实现整个系统，并在屏幕上绘出各点的时域及频域图。
5、 实验不同的噪声强度对系统的影响。
四、 设计步骤
1、 设计滤波器。
2、 绘软件流程图。
3、 软件设计。
4、 软件调试。
五、 程序流程
1、 设计LPF、BPF，得到它们的单位冲激响应h1(n)及h2(n)。画出它们的时域图及频率特性。
2、 由学号的最低四位产生相应的基带信号，以fs对基带信号进行抽样，每个码元用fsT个采样点表示，产生离散的基带信号s(n)，画出s(n)的时域图及频谱。
3、 基带信号进行低通滤波，滤波后的信号b(n)=s(n)*h1(n)。画出b(n)的时域图及频谱。注意：滤波后信号的长度为N＋M－1，M为输入信号的长度，N为滤波器的长度，为了消除滤波器延时特性的影响，可以去掉滤波后的序列的前(N－1)/2点和最后的(N－1)/2点，这样滤波后的序列长度仍然为M。后面的滤波也照此处理。
4、 对b(n)进行调制得到c(n)，c(n)=b(n)cos(2πfcn/fs)，fs为抽样频率。画出c(n)的时域图及频谱。
5、 对b(n)叠加白噪声得到d(n)，d(n)=c(n)+N(n)，N(n)为白噪声。画出d(n)的时域图及频谱。
6、 对d(n)进行带通滤波得到e(n)，e(n)=d(n)*h2，画出e(n)的时域图及频谱。
7、 对e(n)进行相干解调得到f(n)，f(n)=e(n)cos(2πfcn/fs)，画出f(n)的时域图及频谱。
8、 对f(n)进行低通滤波，滤波后的信号g(n)=f(n)*h1(n)。画出g(n)的时域图及频谱。
9、 对g(n)进行判决得到基带信号s1(n)，画出s1(n)的时域图并且与s(n)作比较。
七、 附加题
1、 改变滤波器带宽，观察各个点的信号波形有何变化，从理论上解释观察到的现象。为了避免码元干扰，滤波器应该具有什么特性?
2、 噪声强度多大时有误判决？与理论推导的结果比较。
3、 不同的抽样频率fs对系统有何影响？
4、 滤波器采用不同的阶数对系统有何影响？
5、 用窗函数法设计滤波器，采用不同的抽样位置对系统的性能有何影响？如何确定最佳抽样位置？
6、 在判决前要进行抽样，不同的抽样位置对系统的性能有何影响？如何确定最佳抽样位置？
7、 考察加上纠错编码（如汉明码、BCH码）后对通讯可靠性有什么影响？
8、 选用不同的基带波形（如三角波、升余弦波）对系统有何影响？
9、 如果把2ASK改为4ASK（即基带信号用4进制表示），程序应该如何修改？判决规则是什么？结构如何？
PS：实验图粘不过来了，那个如果回答的时候也遇到相应问题，请回复后给我离线留言，我会提供邮箱的（百度协议规定不能附带邮箱提问），谢谢！
PS又PS：如果能够提供完整答案，我会再追加50-100分不等的，谢谢！

附：
1楼，我要的是全部的过程，而非简单的提示
2楼你找的不是我要的，我要的是用Matlab设计的，而非Systemview

[UsingMatLabsimulationcommunicationprincpleseriesof] - 本毕业设计用Matlab中的建模仿真工具SIMULINK对通信原理实验进行仿真。作为系列实验的第一部分，包括模拟信号的线性调制解调(AM、DSB、SSB)过程、扰码与解扰实验和低通信号的抽样定理实验。论文中讲述了Matlab的基础知识、Simulink仿真操作方法以及在通信系统中的应用，对被仿真实验
[2ASK.rar] - 2ASK调制与解调包含顶层文件，各模块文件和仿真波形
[blooPressure.rar] - 上臂袖带式电子血压计的单片机处理程序和设计说明
[duozhijishu.rar] - 此内容是对多址技术即cdma,fdma,tdma技术的原理详细介绍，然后利用matlab7.0仿真软件进行SIMULINK仿真框图设计，进行仿真实验，对教师教学和学生自学都非常有帮助哦 ！
[ASKPSk.rar] - ASK，PSK，BASK,BPSK的产生程序。用MATLAB来实现的。 参考技术A [UsingMatLabsimulationcommunicationprincpleseriesof] - 本毕业设计用Matlab中的建模仿真工具SIMULINK对通信原理实验进行仿真。作为系列实验的第一部分，包括模拟信号的线性调制解调(AM、DSB、SSB)过程、扰码与解扰实验和低通信号的抽样定理实验。论文中讲述了Matlab的基础知识、 参考技术B 基于Systemview的通信系统的仿真
摘 要
数字通信系统, 按调制方式可以分为基带传输和带通传输。数字基带信号的功率一般处于从零开始到某一频率低频段，因而在很多实际的通信中就不能直接进行传输，需要借助载波调制进行频谱搬移，将数字基带信号变换成适合信道传输的数字频带信号进行传输，这种传输方式，称为数字信号的频带传输或调制传输。数字调制在实现的过程中常采用键控的方法，从几个不同参量的独立振荡源中选参量，由此产生的三种基本调制方式分别称为振幅键控（ASK,Amplitude-Shift keying）、移频键控（FSK ，Frequency-Shift keying）和移相键(PSK,Phase-Shift keying )或差分移相（DPSK,DifferentPhase-Shift keying）。
本文通过Systemview仿真软件，对2ASK、2FSK、2PSK、2DPSK系统进行仿真，分析2ASK、2FSK、2PSK和2DPSK的信号的调制方式，频谱特性，2ASK的相干解调和非相干解调系统、利用Costas环对2FSK、2PSK信号进行解调以及2FSK、2PSK的相干解调系统，并且对2PSK的抗噪声性能做了一定的分析，最后同样用两种方式对2DPSK信号解调，并进行仿真分析。通过对2ASK、2FSK、2PSK和2DPSK系统的分析，对几种调制方式的抗噪声性能、频带利用率及相干解调和非相干解调的抗噪声性能等有了更加清楚的认识。

关键字：2ASK；2FSK；2PSK；2DPSK；相干解调；非相干解调；Systemview

一、绪论
数字通信系统, 按调制方式可以分为基带传输和带通传输。数字基带信号的功率一般处于从零开始到某一频率（如0～6M）低频段，因而在很多实际的通信（如无线信道）中就不能直接进行传输，需要借助载波调制进行频谱搬移，将数字基带信号变换成适合信道传输的数字频带信号进行传输，这种传输方式，称为数字信号的频带传输或调制传输、载波传输。
所谓调制，是用基带信号对载波波形的某参量进行控制，使该参量随基带信号的规律变化从而携带消息。对数字信号进行调制可以便于信号的传输；实现信道复用；改变信号占据的带宽；改善系统的性能。
和模拟调制不同的是，由于数字基带信号具有离散取值的特点，所以调制后的载波参量只有有限的几个数值，因而数字调制在实现的过程中常采用键控的方法，就像用数字信息去控制开关一样，从几个不同参量的独立振荡源中选参量，由此产生的三种基本调制方式分别称为振幅键控（ASK,Amplitude-Shift keying）、
移频键控（FSK,Frequency-Shift keying）和移相键(PSK,Phase-Shift keying )或差分移相键（DPSK,DifferentPhase-Shift keying）。数字调制系统的基本结构如图：

在数字调制中，数字基带信号可以是二进制的，也可以是多进制的，对应的就有二进制数字调制和多进制数字调制两种不同的数字调制，最简单的情况即是以二进制数字基带信号作为调制信号的二进制数字调制，本次课程设计主要针对就是最常用的二进制数字调制方式即二进制振幅键控、移频键控和移相键控三进行系统仿真分析，通过学习Systemview仿真软件，对对三种系统进行仿真，熟悉2ASK、2FSK、2PSK和2DPSK的原理、已调信号的频谱特点和各系统的抗噪声性能。

二、Systemview软件简介
2.1 Systemview软件特点
Systemview是El ANIX公司推出的一个完整的动态系统设计、模拟和分析的可视化软件。他可以提供大量的信号源供系统分析使用；其丰富的算子图符和函数库便于设计和分析各种系统；其多种信号接受器为时域和频域的数值分析提供便捷的途径；其无限制的分层结构使建立大而复杂的系统变得容易；另外他还提供对于外部数据文件的接口，使信号分析更加灵活方便。
Systemview操作简单，使用方便，只要用鼠标从Systemview 库中选择图符并将他们拖拽到设计窗口中连接起来创造线性和非线性，离散和连续，模拟、数字和混合模式的系统，Systemview 的所有图符都有相似的参数定义窗口，我们所要做的只是修改各个图符的参数，无需编程即可实现系统的设计和模拟。
Systemview 的界面直观，设计窗口中各功能模块都用形象直观的图符表示，分析窗口中分析结果以各种图形直观显示，使我们对系统的结构，功能和分析结果一目了然。他的另一个重要特点是可扩展性，Systemview 允许用户插入使用C++编写的用户代码库，插入的用户库自动集成到Systemview 中，能够像内建库一样使用。
Systemview提供了智能化的辅助设计。在系统设计仿真时，Systemview 能自动执行系统连接检查，给出连接错误信息或尚悬空的待连接端信息。通知用户连接出错并通过显示指出出错的图符。并在编译时，给出系统运行的大约时间，方便了设计人员进行调试。其带有的API功能可以利用VC 环境，将系统编译成可脱离Systemview独立运行的可执行文件，大大提高了运行速度和仿真效率。

2.2 使用Systemview进行系统仿真的步骤
使用Systemview进行系统仿真，一般要经过以下几个步骤：
(1)建立系统的数学模型 根据系统的基本工作原理，确定总的系统功能，并将各部分功能模块化，找出各部分的关系，画出系统框图。
(2)从各种功能库中选取、拖动可视化图符，组建系统在信号源图符库、算子图符库、函数图符库、信号接受器图符库中选取满足需要的功能模块，将其图符拖到设计窗口，按设计的系统框图组建系统。
(3)设置、调整参数，实现系统模拟参数设置包括运行系统参数设置(系统模拟时间，采样速率等)和功能模块运行参数(正弦信号源的频率、幅度、初相，低通滤波器的截止频率、通带增益、阻带衰减等)。
(4)设置观察窗口， 分析模拟数据和波形 在系统的关键点处设置观察窗口，用于检查、监测模拟系统的运行情况，以便及时调整参数，分析结果。

三、二进制频移键控（2FSK）
3.1 二进制频移键控（2FSK）的基本原理
FSK是在数字信号调制中使用较典型的一种调制方式,其利用载波的频率变化来传递数字信息0 或1. 由于其实现起来较容易、抗噪声与抗衰减的性能较好,因此,在中低速数据传输(传输速率在1 200 bit/ s 以下) 中得到了广泛的应用.在二进制FSK中载波频率随着调制信号1或0而变,1 对应于载波频率f1,0对应于载波频率f2 .二进制FSK已调信号的时域表达式为:
S2FSK( t) = ∑nang(t-nTS )cosω1t +∑na-ng(t- nTS)cosω2t其中：ω1 = 2πf1，ω2 = 2πf2
an =0 概率为P a-n = 1 概率为P
1 概率为1–P 0 概率为1 - P
式中：a-n—an 的反码；g—码元波形；TS—码元周期f1、f2 —2FSK的两个不同的载波频率.
3.1.1 2FSK调制的方法
同2ASK调制的方法相同，2FSK也有两种调制方式：模拟调频法，如图3.1.1-1（a）和数字键控的方法，如图3.1.1-1（b），
图3.1.1-1 2FSK信号产生的方法
由3.1.1-1（b）可得2FSK的表达式如下：

数字键控法实现二进制移频键控信号的原理图如下 ：

图3.1.1-2数字键控法实现2FSK信号的原理图

由上图可得二进制移频键控信号的时间波形如下：

图3.1.1-3 2FSK信号的时间波形

可得2FSK的时域表达式如下：

（2）2FSK信号的解调
3.1.2 2FSK解调的方法

图3.1.2-1 2FSK信号非相干解调

3.2 使用Systemview软件对2FSK系统进行仿真
3.2.1 2FSK信号的产生
调频法:在SystemView 中二进制数据用伪随机序列PNSeq仿真出随机的0 ,1 二进制数字信号,通过调频器FM 调制,0 对应50 Hz ,1 对应100 Hz.幅度A 均为1 V.
键控法:在SystemView中二进制数据用伪随机序列PNSeq仿真出随
机的0,1二进制数字信号,作为键控开关的控制信号，0 对应50 Hz 正弦波,1对应100 Hz 正弦波. 幅度A 均为1V.

（1）调频法产生2FSK信号

图3.2.1-1 调频法实现2FSK信号

仿真结果如下：

图3.2.1-2 2FSK信号波形图

（1）键控法产生2FSK信号

图3.2.1-3数字键控法实现2FSK信号
分析：
系统的参数设计如下：Token0为调制信Amplitude=-0.5v,
Offset=0.5v,Rate=10Hz,Levels=2,Phase=0，Token1、3为载波，载波1频率=50HZ，载波3频率=100HZ。 Token2、4为乘法器Token7为Adder。 Token6为反相器，系统运行时间为0.3S，采样频率=20000HZ。

仿真分析如下：

图3.2.1-4 2FSK信号波形
分析：
从上到下依次是调制信号波形、频率为f1的已调信号波形，频率为f2的已调信号波形，2FSK信号波形。由图中可以观察到2FSK信号就是两个2ASK信号叠加而成.。
3.2.2 2FSK信号的频谱图

图3.2.2-1 2FSK信号的离散频谱图
分析：
在观察2FSK信号的频谱图时将载波的频率改为f1=2500HZ f2=5000HZ，得如图3.2.1-3所示2FSK信号的频谱
从上到下，从左到右上图依次是调制信号的频谱图，已调信号的频谱图，频率为f1已调信号的频谱图，频率为f1已调信号的频谱图。由于FFT频谱是对称的，故图中只画出了前一半。分析图3.2.1-3可得2FSK信号频谱特性如下：
2FSK信号频谱特性：由连续谱和离散谱两部分组成。连续谱由两个双边谱叠加而成，而离散谱则出现在两个载频上。若两个载频之差较小，如小于fs,则连续谱出现单峰；若载频之差逐步增大，则连续谱将出现双峰。2FSK是非线性调制。
2FSK信号带宽为：

3.2.3 2FSK非相干解调系统
（1）2FSK非相干解调系统框图如下：

图3.2.3-1 2FSK非相干解调系统框图
分析：
设计解调电路时,先用中心频率为500Hz 和1kHz的两个带通滤波器将已调信号滤成两路并联信号。这里选用通带分别为480～520Hz 和980～1020Hz 的Chebyshev 带通滤波器。接下来选用合适的器件实现包络检波器的功能。包络检波法解调方法,包络检波器可由半波整流器(Half Rctfy) 与低通滤波器串联实现其功能。半波整流器的功能描述是y ( t) = x ( t) - z , x ( t) ≥z其中, y ( t) 为输出信号, x ( t ) 为输入信号, z 为所设置的零点。当z 取0 时,其功能为：y ( t) =x ( t)； x ( t) ≥0
0 ； x ( t) < 0
低通滤波器选用Chebyshev 模拟滤波器,截止频率设置为20 Hz。这样设置后通过包络检波的两路信号波形如图3.2.2-1所示。在图5 中,上面一路信号为带通滤波器中心频率为500Hz 的那路信号;下面一路信号为带通滤波器中心频率为1000 Hz 的那路信号,再经过包络检波后的两路信号的高低电平。在图3.2.2-1中,因为这里的抽样判决器是判定哪一个输入样值大, 可以选用逻辑库中的模拟比较器(AnaCmp) 来进行抽样判决。AnaCmp 是一个两端输入一端输出的逻辑器件。选择输出时,其逻辑功能是当INPUT + > = INPUT - 时,输出高电平的值;当INPUT +< INPUT - 时,输出低电平的值。当选择Q 输出时,其逻辑功能是当INPUT + > = INPUT - 时,输出低电平的值;当INPUT + < INPUT - 时,输出高电平的值。将两路信号接入,高低电平值分别设置为1 V 和-1 V ,选择输出,输出的信号就将是解调信号【图3.2.2-2中（c）】 。

波形仿真结果如下：

图3.2.3-2 2FSK非相干解调波形（a）
分析：
从上到下，从左到右依次是调制信号波形、本地载波波形、经过中心频率为f1的带通滤波器后的波形、经过中心频率为f2的带通滤波器后的波形。

图3.2.3-2 2FSK非相干解调波形（b）
分析：
从上到下，从左到右依次是经过中心频率为f1的带通滤波器后的波形、频率为f1的信号半波整流后的波形、经过中心频率为f2的带通滤波器后的波形、频率为f2的信号半波整流后的波形。

图3.2.3-2 2FSK非相干解调波形（c）
分析：
从上到下，从左到右依次是频率为f1的信号经过低通滤波i器后的波形、频率为f2的信号经过低通滤波i器后的波形、调制信号的波形、已调信号的波形。
3.2.4 2FSK锁相鉴频法解调系统
调制采用“载波调频法”产生2FSK信号，解调采用“锁相鉴频法”。系统组成如图3.2.4-1所示。

根据图3.2.4-1所示系统，在SystemView系统窗下建立仿真系统，首先设置时间窗，运行时间：0.3秒，采样速率：20000Hz，组成系统如图3.2.4-2所 示，

3.2.4-2 2FSK锁相鉴频法解调系统框图

其中：
Token0：PN码源，参数：Amp＝1v、Offset＝0v、Rate＝10Hz、No.of levels＝2；
Token1：直接调频器，参数：Amp＝1v、F＝1700Hz、Phase＝0、Mod Gain＝400Hz/V；
Token5，6，4：锁相环路，其中Token6为Butterworth_LPF、No.of Poles＝1、Lo Cuttoff＝1200Hz； Token5：VCO，参数：Amp=2v、F=1700Hz、Phase=0、Mod Gain=800Hz/v；
Token8：低通滤波器，参数：Butterworth_BPF、No.of Poles＝7、Lo Cuttoff＝2400Hz；
Token14：过零比较器，参数：选a>b模式、a输入为Token8输出、b输入为门限电平、 True Output＝1v、false Output＝-1v ；
Token15：比较门限电平，选正弦信号源，Amp＝0V、F＝0Hz，即比较门限为0电平；
Token10，11，16，17，13：信宿接收分析器Sink。
仿真结果如下图：

3..2.4-3 2FSK锁相鉴频法解调波形图
分析：从上到下，从左到右波形图依次是基带信号、解调信号、滤波1输出信号、滤波2输出信号.

四、二进制振幅键控（2ASK）
4.1、二进制振幅键控的基本原理
2ASK信号时间波形e(t)随二进制基带信号是s(t)的通断的变化，如下图g(t)、s(t)、e(t)如下图

图4.1-1 2ASK信号时间波形

（1）2ASK信号的解调方法通常有两种，如下图：

图4.1—2

（2）e(t)的功率谱密度为：

单极性随机脉冲序列功率谱密度的一般表达式为：

得e（t）的功率谱为：

4.2 Systemview软件对2ASK系统进行仿真
4.2.1 2ASK调制系统
①2ASK调制系统框图如下：

图4.2.1-1 2ASK调制系统
分析：如下图2ASK调制的方法通常有两种：一般模拟幅度的调制方法，如图4.2.1-2（a）和数字键控的方法，如图4.2.1-2（a），图中开关受s（t）的控制；
图4.2.1-2 2ASK调制的方法

②仿真分析：

图4.2.1-3 2ASK信号波形
4.2.2 2ASK频谱及功率谱

图4.2.1-1 2ASK频谱及功率谱
分析：
上图中从上到下，从左到右依次是基带信号频谱，已调信号的频谱，调制信号的功率谱和已调信号的功率谱。由于FFT频谱是对称的，故图中只画出了前一半。分析图2.2.1-4可得2ASK频谱特性如下：
2ASK频谱特性：①由连续谱和离散谱两部分组成。连续谱取决于g(t)经线性调制后的双边带谱，离散谱由载波分量决定。②2ASK信号的频谱只是将基带信号的频谱沿频率轴平移了一个fc,而基带信号的频谱结构并不改变。③基带信号带宽为fs,2ASK信号带宽为2fs。频带利用率仅为直接传输基带信号的1/2。
4.2.3 2ASK相干解调的系统

图4.2.3-1 2ASK相干解调的系统框图
分析：
系统的参数设计如下：Token1、3为乘法器，Token2、6为载波，载波频率=1000HZ， Token4为Adder为高斯脉冲形成滤波器；Token5为高斯噪声产生器，设标准偏差 Std Deviation=0.3v，均值Mean=0v；Token7为模拟低通滤波器，来自选操作库中的“LinearSys”图符按钮，在设置参数时，将出现一个设置对话框，在“Design”栏中单击Analog…按钮，进一步单击“Filter PassBand”栏中Lowpass按钮，选择Butterworth型滤波器，设置滤波器极点数目：No.of Poles=5（5阶），设置滤波器截止频率：LoCuttoff=200 Hz。Token11为基带信号，频率=50HZ，电平=2，偏移=1
系统运行时间为0.3S，采样频率=20000HZ。

仿真结果如下：

图4.2.3-2 2ASK相干解调波形
分析：上图的结果依次是基带信号、已调信号和解调信号

4.2.4 ASK非相干解调的系统

（1）2ASK非相干解调的系统的框图如下：
①
图4.2.4-1 2ASK非相干解调的系统的框图
系统的参数设计如下：
Token1、3为乘法器，Token2、6为载波，载波频率=1000HZ， Token4为Adder为高斯脉冲形成滤波器；Token5为高斯噪声产生器，设标准偏差 Std Deviation=0.3v，均值Mean=0v；Token7为模拟低通滤波器，来自选操作库中的“LinearSys”图符按钮，在设置参数时，将出现一个设置对话框，在“Design”栏中单击Analog…按钮，进一步单击“Filter PassBand”栏中Lowpass按钮，选择Butterworth型滤波器，设置滤波器极点数目：No.of Poles=5（5阶），设置滤波器截止频率：LoCuttoff=200 Hz。Token11为基带信号，频率=50HZ，电平=2，偏移=1
系统运行时间为0.3S，采样频率=20000HZ。

② 仿真结果如下：

图4.2.4-2 2ASK非相干解调的波形
分析：上图的结果依次是基带信号、已调信号和解调信号

五、二进制移相键控（2PSK）
5.1 二进制移相键控（2PSK）的基本原理
2PSK,二进制移相键控方式，是键控的载波相位按基带脉冲序列的规律而改变的一种数字调制方式。就是根据数字基带信号的两个电平(或符号)使载波相位在两个不同的数值之间切换的一种相位调制方法。两个载波相位通常相差180度，此时称为反向键控(PSK),也称为绝对相移方式。

（1）2PSK信号的产生
2PSK的产生：模拟法和数字键控法，就模拟调制法而言，与产生2ASK信号的方法比较，只是对s(t)要求不同，因此2PSK信号可以看作是双极性基带信号作用下的DSB调幅信号。而就键控法来说，用数字基带信号s(t)控制开关电路，选择不同相位的载波输出，这时s(t)为单极性NRZ或双极性NRZ脉冲序列信号均可。
2PSK信号与2ASK信号的时域表达式在形式上是完全相同的，所不同的只是两者基带信号s(t)的构成，一个由双极性NRZ码组成，另一个由单极性NRZ码组成。因此，求2PSK信号的功率谱密度时，也可采用与求2ASK信号功率谱密度相同的方法。

（2）2PSK信号的功率谱
2PSK信号的功率谱密度 及其功率谱示意图如下:

分析2PSK信号的功率谱：（1）当双极性基带信号以相等的概率（p=1/2）出现时，2PSK信号的功率谱仅由连续谱组成。而一般情况下，2PSK信号的功率谱由连续谱和离散谱两部分组成。其中，连续谱取决于基带信号经线性调制后的双边带谱，而离散谱则由载波分量确定（2）2PSK的连续谱部分与2ASK信号的连续谱基本相同因此，2PSK信号的带宽、频带利用率也与2ASK信号的相同
其中， 数字基带信号带宽。这就表明，在数字调制中，2PSK的频谱特性与2ASK相似。相位调制和频率调制一样，本质上是一种非线性调制，但在数字调相中，由于表征信息的相位变化只有有限的离散取值，因此，可以把相位变化归结为幅度变化。这样一来，数字调相同线性调制的数字调幅就联系起来了，为此可以把数字调相信号当作线性调制信号来处理了。
（3）2PSK的解调系统
①2PSK信号属于DSB信号,它的解调,不再能采用包络检测的方法,只能进行相干解调。2PSK相干解调系统框图及个测试行波形如下：
5.1-1 2PSK相干解调系统框图及个测试点波形
②利用Costas环对2PSK信号进行解调
2PSK 调制和Costas环解调系统组成如下图所示：

5.1.-2 2PSK 调制和Costas环解调系统组成
5.2 Systemview软件对2PSK系统进行仿真
5.2.1 2PSK信号的产生

5.2.1-1 键控法产生2PSK信号框图
分析：
键控法产生2PSK信号，用数字基带信号s(t)控制开关电路，选择不同相位的载波输出，这时s(t)为单极性NRZ或双极性NRZ脉冲序列信号均可。

仿真结果如下：

4.2.1-2 2PSK信号的波形
分析：
2PSK信号与2ASK信号的时域表达式在形式上是完全相同的，所不同的只是两者基带信号的构成，一个由双极性NRZ码组成，另一个由单极性NRZ码组成。

5.2.2 2PSK相干解调系统

5.2.2-1 2PSK相干解调系统框图
分析：2PSK信号相干解调的过程实际上是输入已调信号与本地载波信号进行极性比较的过程，故常称为极性比较法解调。由于2PSK信号实际上是以一个固定初相的末调载波为参考的，因此，解调时必须有与此同频同相的同步载波。如果同步载波的相位发生变化，如0相位变为π相位或π相位变为0相位，则恢复的数字信息就会发生“0”变“1”或“1”变“0”，从而造成错误的恢复。这种因为本地参考载波倒相，而在接收端发生错误恢复的现象称为“倒π”现象或“反向工作”现象。绝对移相的主要缺点是容易产生相位模糊，造成反向工作。这也是它实际应用较少的主要原因。
仿真结果如下：

图5.2.2-2 2PSK相干解调系统框图
分析：以上波形从上到下依次是调制信号波形、2PSK波形、相乘输出波形、滤波后的波形、解调出的波形。

5.2.3 2PSK 调制和Costas环解调系统组成

图5.2.3-1 2PSK 调制和Costas环解调系统框图

仿真结果如下：

图5.2.3-2 2PSK Costas环解调出波形
分析：
从上到下依次是：调制信号波形、低通滤波后的波形、解调出的波形。
5.2.4 2PSK信号的频谱和功率谱

图5.2.4 2PSK信号的频谱和功率谱
分析：
2PSK信号的功率谱特点：（1）当双极性基带信号以相等的概率（p=1/2）出现时，2PSK信号的功率谱仅由连续谱组成。而一般情况下，2PSK信号的功率谱由连续谱和离散谱两部分组成。其中，连续谱取决于数字基带信号s(t)经线性调制后的双边带谱，而离散谱则由载波分量确定。 （2）2PSK的连续谱部分与2ASK信号的连续谱基本相同（仅差一个常数因子）。因此，2PSK信号的带宽、频带利用率也与2ASK信号的相同

5.2.5 误比特率BER分析
（1）原理：误比特率（BER：Bit Error Rate）是指二进制传输系统出现码传输错误的概率，也就是二进制系统的误码率，它是衡量二进制数字调制系统性能的重要指标，误比特率越低说明抗干扰性能越强。对于多进制数字调制系统，一般用误符号率（Symble Error Rate）表示，误符号率和误比特率之间可以进行换算，例如采用格雷编码的MPSK系统，其误比特率和误符号率之间的换算关系近似为： 其中，M为进制数，且误比特率

小于误符号率。
（2）2PSK系统BER分析的仿真分析系统

图5.2.5-1 2PSK系统BER分析的仿真分析系统

编
号 图符块属性
（Attribute） 类型
（Type） 参数设置
（Parameters）
0 Source PN Seq Amp=1v, Offset=0v, Rate=50Hz, Level=2
3、.6 Source Sinusoid Amp=1v, Freq=1000Hz, Phase= 0 deg
4 Source Gauss Noise Pwr Density=0.007W/Hz, Mean=0v,
System=50 ohms
13 Operator Gain Gain Unit=dB Power, Gain=-30dB
5 Operator Linear Sys Butterworth, Lowpass IIR, 5 Poles, Fc=200Hz
1 Operator Sampler Interpolating, Rate=50Hz
21 Comm BER Rate No.Trials=3 bits, Threshoid=0v, Offset=1 Sec
18 Operator Smpl Delay Fill Last register, Delay=1 samples
19 Operator Sampler Interpolating, Rate=50Hz
14 Sink Final Value -- （终值显示图符块）
15 Fuction Cmlty Avg Gain=1 （累积平均图符块）
17 Sink Analysis -- （观察叠加的高斯噪声每次循环的强度变化）
（3）仿真分析：

图5.2.5-2 叠加高斯噪声强度随循环每次减小3dB变化

图5.2.5-3 随解调信号SNR改变的BER曲线

分析：
输入的2PSK信号功率保持不变，而叠加的高斯噪声功率逐次衰减，即SNR不断增加。系统的误信率一直在下降。

数字信号调制基于matlab GUI数字信号调制系统（2ASK+2FSK+2PSK+4ASK+4FSK+4PSK带面板）含Matlab源码 1658期

一、数字信号调制系统简介

二进制数字信号调制原理
数字调制是指用数字基带信号对载波的某些参量进行控制, 使载波的这些参量随基带信号的变化而变化。在通信系统中, 作为载波的正弦波有幅度、频率和相位3个参数, 对应的也就有3种基本的调制方式:调幅、调频和调相。由于数字信号不同与模拟信号的特殊性, 在数字载波通信中, 这3种基本的调制方式分别被称为幅移 (ASK) 、频移键控 (FSK) 和相移键控 (PSK) 。调制信号是二进制数字基带信号时, 这种调制称为二进制数字调制。在二进制数字调制中, 载波的幅度、频率和相位只有两种变化方式。

1 ASK调制
振幅键控是利用载波的幅度变化来传递数字信息, 而其频率和初相位保持不变。二进制幅度键控 (2ASK) 方式是数字调制方式中出现最早也是最简单的一种方法。这种方法最初用于电报系统, 二进制振幅键控常常作为研究其它数字调制方式的基础。2ASK调制信号只有0或1两个电平相乘的, 结果相当于将载频或者关断, 或者接通, 它的实际意义是当调制的数字信号为“1”时, 传输载波;当调制的数字信号为“0”时, 不传输载波。

2ASK信号的一般表达式为:

其中

2 FSK调制
频移键控是利用载波的频率变化来传递数字信息。在2FSK中, 载波的频率随二进制基带信号在f1和f0的两个频率点变化。它的实际意义是当调制的数字信号为“1”或“0”时传输f1或f2频率的载波。

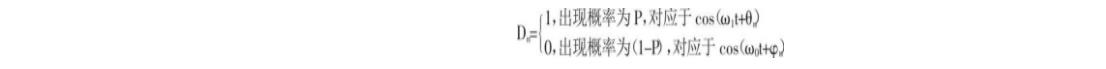
其中ω1=2nf1, ω0=2nf0, θn为频率为f1的载波的初始相位, φn为频率为f0的载波的初始相位。令 为Dn的反码, 即

则2FSK信号可表示为:

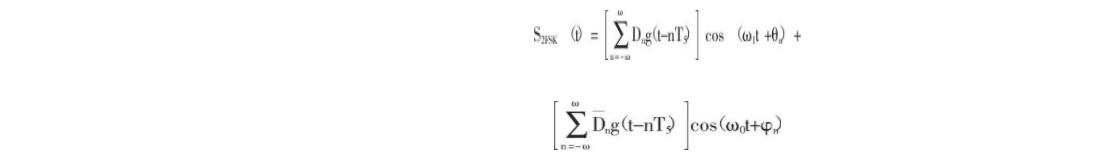
3 PSK调制
相移键控是利用载波的相位变化来传递数字信息, 而振幅和频率保持不变。PSK调制时, 载波的相位随调制信号状态不同而改变。如果两个频率相同的载波同时开始振荡, 这两个频率同时达到正最大值, 同时达到零值, 同时达到负最大值, 此时它们就处于“同相”状态;如果一个达到正最大值时, 另一个达到负最大值, 则称为“反相”。一般把信号振荡一次 (一周) 作为360度。如果一个波比另一个波相差半个周期, 我们说两个波的相位差180度, 也就是反相。当传输数字信号时, “1”码控制发0度相位, “0”码控制发180度相位。相移键控有很好的抗干扰性, 在有衰落的信道中也能获得很好的效果。

二、部分源代码

function varargout = xhcl(varargin)
% XHCL MATLAB code for xhcl.fig
%      XHCL, by itself, creates a new XHCL or raises the existing
%      singleton*.
%
%      H = XHCL returns the handle to a new XHCL or the handle to
%      the existing singleton*.
%
%      XHCL('CALLBACK',hObject,eventData,handles,...) calls the local
%      function named CALLBACK in XHCL.M with the given input arguments.
%
%      XHCL('Property','Value',...) creates a new XHCL or raises the
%      existing singleton*.  Starting from the left, property value pairs are
%      applied to the GUI before xhcl_OpeningFcn gets called.  An
%      unrecognized property name or invalid value makes property application
%      stop.  All inputs are passed to xhcl_OpeningFcn via varargin.
%
%      *See GUI Options on GUIDE's Tools menu.  Choose "GUI allows only one
%      instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help xhcl

% Last Modified by GUIDE v2.5 07-Jan-2022 15:44:18

% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',       mfilename, ...
                   'gui_Singleton',  gui_Singleton, ...
                   'gui_OpeningFcn', @xhcl_OpeningFcn, ...
                   'gui_OutputFcn',  @xhcl_OutputFcn, ...
                   'gui_LayoutFcn',  [] , ...
                   'gui_Callback',   []);
if nargin && ischar(varargin1)
    gui_State.gui_Callback = str2func(varargin1);
end

if nargout
    [varargout1:nargout] = gui_mainfcn(gui_State, varargin:);
else
    gui_mainfcn(gui_State, varargin:);
end
% End initialization code - DO NOT EDIT


% --- Executes just before xhcl is made visible.
function xhcl_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
% varargin   command line arguments to xhcl (see VARARGIN)

% Choose default command line output for xhcl
handles.output = hObject;

% Update handles structure
guidata(hObject, handles);

% UIWAIT makes xhcl wait for user response (see UIRESUME)
% uiwait(handles.figure1);


% --- Outputs from this function are returned to the command line.
function varargout = xhcl_OutputFcn(hObject, eventdata, handles) 
% varargout  cell array for returning output args (see VARARGOUT);
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout1 = handles.output;


% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global sj;
N_m = 10;%随机信号长度
sj= randi([0,1],1,N_m);
t_begin=0;
t_end=1;
mt=0;
t=0:0.01:10;
for i=1:length(sj)
    if(sj(i)==1);
        mt=mt+1.*(t>=t_begin&t<t_end);
    else
        mt=mt+0.*(t>=t_begin&t<t_end);
    end
    t_begin=t_begin+1;
    t_end=t_end+1;
end
axes(handles.axes1);
plot(t,mt);

% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton2 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global sj;
t_begin=0;
t_end=1;
ASK2=0;
t=0:0.01:10;
for i=1:length(sj)
%     t=t_begin:0.01:t_end
    if(sj(i)==1)
        ASK2=ASK2+sin(2*pi*t).*(t>=t_begin&t<t_end);
    else
        ASK2=ASK2+0.*(t>=t_begin&t<t_end);
    end
    t_begin=t_begin+1;
    t_end=t_end+1;
end
axes(handles.axes3);
plot(t,ASK2);

% --- Executes on button press in pushbutton3.
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton3 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global sj;
t_begin=0;
t_end=1;
FSK2=0;
t=0:0.01:10;
for i=1:length(sj)
    if(sj(i)==1)
        FSK2=FSK2+sin(4*pi*t).*(t>=t_begin&t<t_end);
    else
        FSK2=FSK2+sin(2*pi*t).*(t>=t_begin&t<t_end);
    end
    t_begin=t_begin+1;
    t_end=t_end+1;
end

axes(handles.axes3);
plot(t,FSK2);

% --- Executes on button press in pushbutton4.
function pushbutton4_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton4 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global sj;
t_begin=0;
t_end=2;
PSK4=0;
t=0:0.01:10;
for i=1:2:length(sj)

    if(sj(i)==1)
        if(sj(i+1)==1)
            PSK4=PSK4+sin(2*pi*t+1.5*pi).*(t>=t_begin&t<t_end);
        else
            PSK4=PSK4+sin(2*pi*t+pi).*(t>=t_begin&t<t_end);
        end
   else
        if(sj(i+1)==1)
            PSK4=PSK4+sin(2*pi*t+0.5*pi).*(t>=t_begin&t<t_end);
        else
            PSK4=PSK4+sin(2*pi*t).*(t>=t_begin&t<t_end);
        end
    end
    t_begin=t_begin+2;
    t_end=t_end+2;
end

三、运行结果

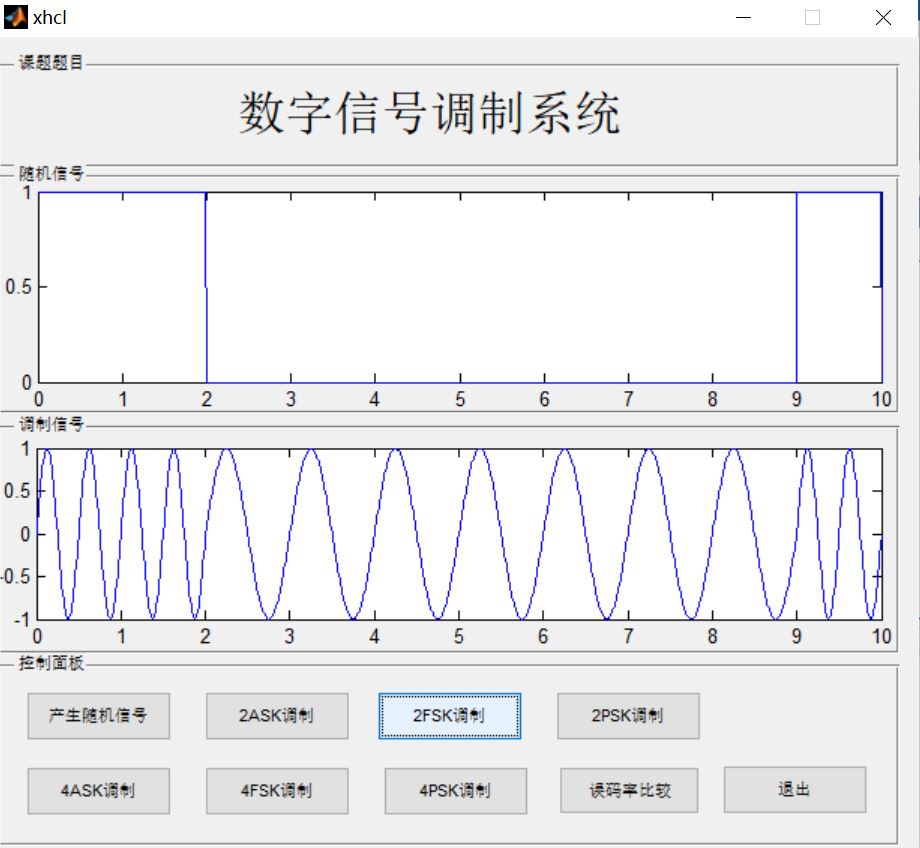
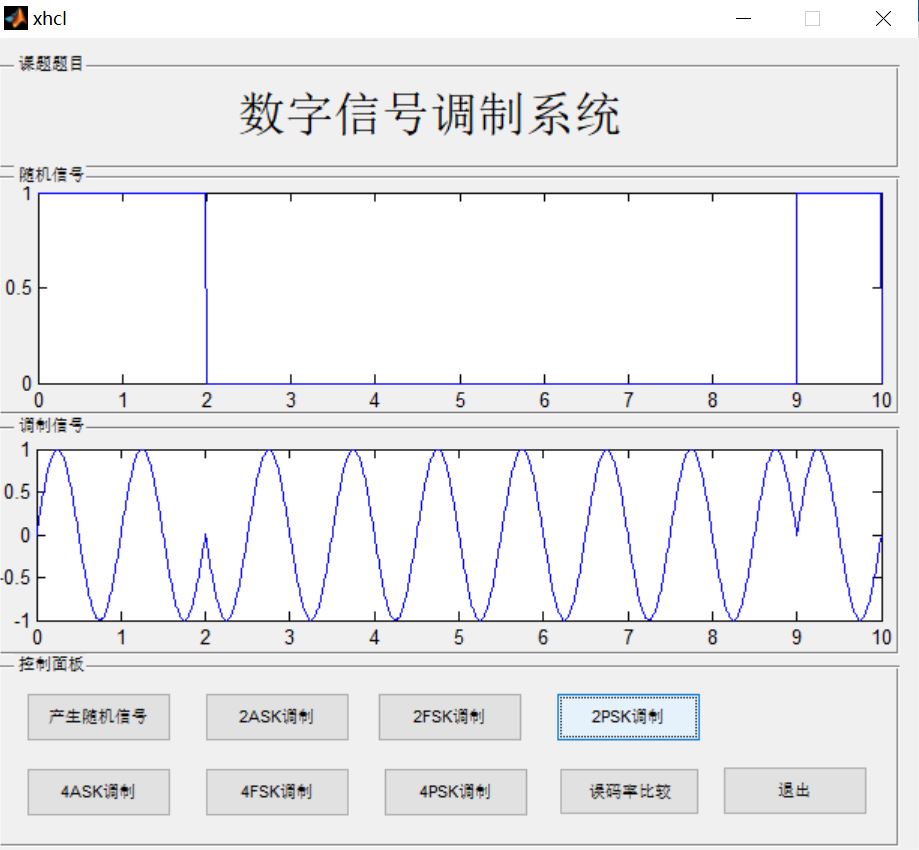
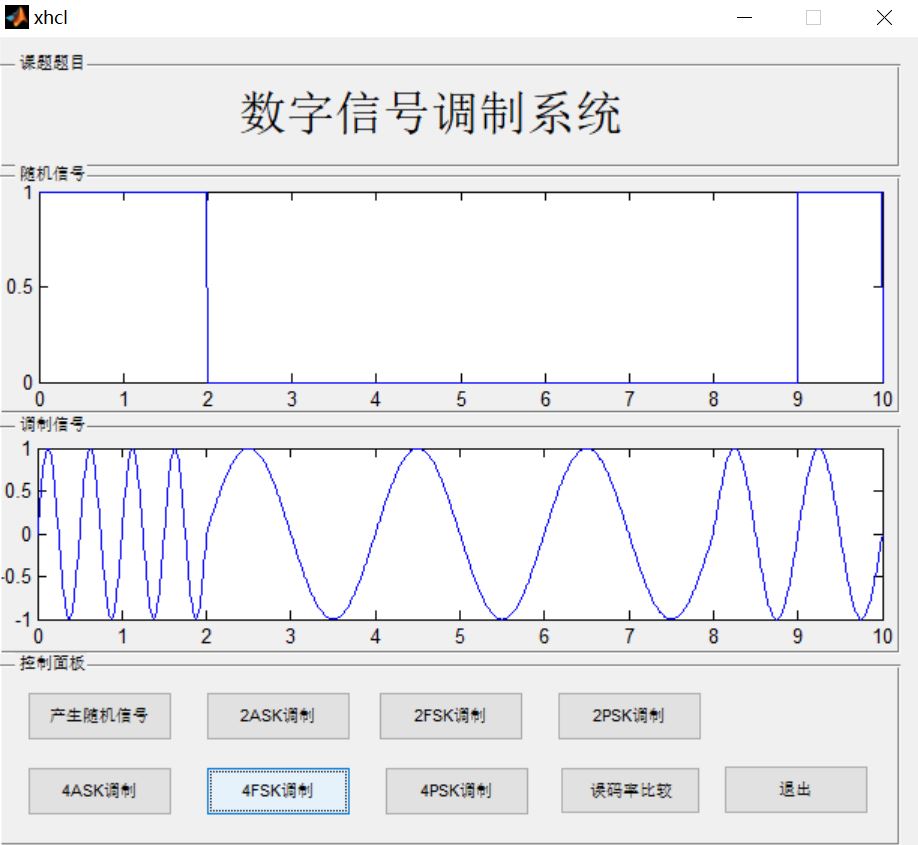
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社，2015.
[2]高宝建,彭进业,王琳,潘建寿.信号与系统——使用MATLAB分析与实现[M].清华大学出版社，2020.
[3]王文光,魏少明,任欣.信号处理与系统分析的MATLAB实现[M].电子工业出版社，2018.
[4]曾祥龙,梁清梅,索丽敏.运用MATLAB实现对数字信号调制的仿真[J].黑龙江科技信息. 2009,(32)