15. 偏差-方差权衡（续）

Posted 2022-11-02 starrow

以K近邻回归模型为例，说明偏差-方差权衡。某数据点的预测函数值为该点K个最近邻实例输出的平均值：

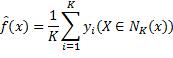
因此预测函数的方差等于：

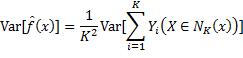
因为各实例的输出Yi是独立的随机变量，且它们的方差都等于σ^2，所以

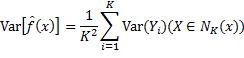
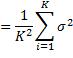
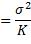
可见，当K增加时，预测函数的方差减少。另一方面，当K增加时，预测所用的外围实例距中心的查询数据点越来越远，因而越来越不相似，将这些实例的平均值作为预测函数值，导致其与理论预测函数值之差，即预测函数的偏差，越来越大。总而言之，在K近邻回归中，用于预测的实例越多，偏差越大，波动性越小；反之，预测的偏差减小，但波动增大。

K的大小还会影响预测函数的复杂度。当K增加时，预测函数在邻近数据点的函数值趋同，函数呈现趋于平滑的倾向，函数的复杂度相应减少。以多项式函数为例，曲线的曲折越少，对应多项式的阶数就越低。K的大小对分类模型也有类似的影响。分类模型的偏差随K递增，波动性随K递减。在输入空间上形成的划分类别的界面，当K增加时，越来越平滑；当K减少时，越来越曲折，等到K降为1时，输入空间就被割裂成大量碎片。

用K近邻模型揭示的规律具有普遍性。一般而言，模型对训练数据的拟合越充分，预测函数越复杂，预测的波动性就越大，偏差就越小；对训练数据的拟合程度越低，预测函数越简单，预测的波动性就越小，偏差就越大。作为统计总体中的一个样本，训练数据集包含哪些实例是随机的。对于确定的输入值，输出又因为噪声带有随机性。假如模型对训练数据过度拟合，相当于过度关注特定样本中输入和输出之间的关系，就会偏离统计总体中输入与输出之间的关系，导致预测随训练数据的变化而剧烈波动，称为过拟合（Overfitting）。欠拟合（Underfitting）与之相反，模型过于粗疏，对训练数据的拟合不足，在训练数据上的预测误差太大。虽然当训练数据变化时，其预测较稳定，但由于与理论预测函数偏差过大，预测误差仍然很大。

许多模型都有调节参数（Tuning parameter），调整它们的值能改变模型的拟合程度和复杂度。通过比较不同复杂度的预测函数在训练数据和测试数据上的表现，能清晰体现偏差与方差的消长。函数越复杂，在训练数据上的误差就越小，在测试数据上的误差则会如U形曲线先减小后增大。前者很好理解，预测函数对训练数据的拟合程度越高，误差就越小；后者是因为预测函数在测试数据上的误差包含了偏差和方差两个竞争因素，拟合程度开始提高时，偏差减少比方差增加多，所以总的误差减小，随着拟合越来越充分，偏差的减小量抵不上方差的增加量，误差开始增大。对模型进行交叉验证有助于取得偏差与方差之间的均衡。

过拟合比欠拟合容易发生，因此发展出许多避免过拟合的技术。其中有一类称为正则化（Regularization），通过缩减模型的参数限制拟合的程度。此处的参数是指模型建立过程中的未知量，需要用训练数据估算其值后模型才能够应用，为与前面提到的调节参数区别，不妨称为模型参数。下文提到参数时，若不强调是调节参数，都是指模型参数。正则化的原理为模型的复杂程度与参数数量成正比，参数调整各输入对输出的贡献，减少参数使模型的输出值免受某些输入的影响，缩小参数值也能减小模型的拟合程度。常用的正则化方法是在损失最小化的目标函数中加入对参数大小的惩罚项，3.3节将详细讨论。另一条途径是在最大后验估计中设置参数特定的先验分布，2.6.3节会给出例子。

偏差与方差的关系能从另一个角度解释，为什么在高维空间不宜采用K近邻模型。向量空间中两点间的距离平方等于其各维度坐标之差的平方和，输入空间的维数越大，以查询数据点为球心，相同半径的球面内包含的训练数据点就越少，查询数据点到K个最近邻的距离就越大，导致预测的偏差增大。

值得一提的是，K近邻模型中的K不是模型参数，而是调节参数。每个具有K个最近邻的区域内预测的输出都相同，因此区域的数量才是模型的参数。假设这些区域互不重叠，其数量为n/K。所以当K增大时，参数减小，与模型的复杂度下降一致。