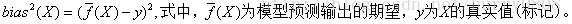模型方差与偏差

Posted 2023-04-05

参考技术A 面试过程中经常会被问到关于方差和偏差的概念以及比对。

偏差度量了学习算法的期望预测值与真实结果间的偏离程度，也就是刻画了模型本身的拟合能力，也就是偏差越大，意味着预测值越偏离真实数据。

最直观的感受就是，如果训练误差很大，测试误差与训练误差相当，那么此时表明模型对训练数据的拟合并不是很好，这就是高偏差。

方差刻画了同样大小训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。说白了就是对预测值方差的描述，方差越大，则数据的分布越分散。

如果训练误差远高于测试误差，那么说明模型过拟合，此时表明模型的方差较高；

偏差和方差不能同时满足。

在模型训练初期，由于迭代轮数较小，此时算法未能完全学习到训练集数据的内容，因此，此时模型的泛华错误率主要来自偏差，而随着轮数不断加深，算法完全拟合了训练集，学习到了训练集数据的波动规律，此时主要泛化错误率来自于方差。而再随着迭代的加深，训练数据的非全局性，非代表性的规律被学习到后，此时发生一点数据波动，模型都会被严重影响，此时可能发生了过拟合。

刻画了任何一种学习算法在该数据集上所能达到的期望泛化误差的下界，也就是刻画了学习问题本身的难度。

其实上述是指标共同构成的是泛化性能的大小，也就是说，泛化性能是由该算法的能力、数据的好坏以及学习任务本身的难度所共同决定的。给定一个学习任务，为了取得较好的泛化性能，需使得偏差较小，即能够充分拟合数据，同时要使得方差较小，也就是数据扰动带来的影响尽量小。

https://www.jianshu.com/p/ed9abdb0c867

偏差与方差，欠拟合与过拟合的关系

偏差(Bias)

偏差指预测输出与真实标记的差别，记为：

偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。

方差(Variance)

方差指一个特定训练集训练得到的函数，与所有训练集得到平均函数的差的平方再取期望，记为：

方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。方差表示所有模型构建的预测函数，与真实函数的差别有多大。

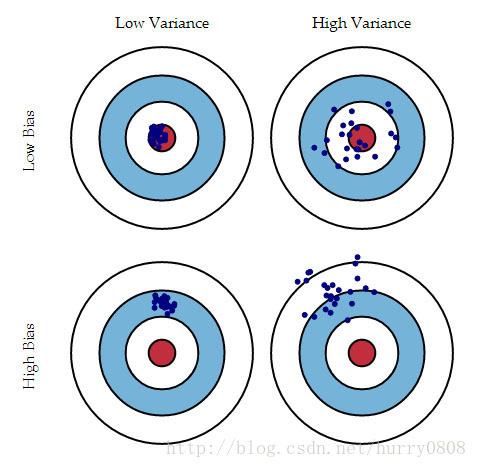
偏差-方差示意图

偏差与方差的区别可用如下的靶标图来说明：

低偏差低方差时，是我们所追求的效果，此时预测值正中靶心(最接近真实值)，且比较集中(方差小)。
低偏差高方差时，预测值基本落在真实值周围，但很分散，此时方差较大，说明模型的稳定性不够好。
高偏差低方差时，预测值与真实值有较大距离，但此时值很集中，方差小；模型的稳定性较好，但预测准确率不高，处于“一如既往地预测不准”的状态。
高偏差高方差时，是我们最不想看到的结果，此时模型不仅预测不准确，而且还不稳定，每次预测的值都差别比较大