14. 偏差-方差权衡

Posted 2023-01-06 starrow

2.5 偏差-方差权衡

在根据训练数据拟合出预测函数后，通过分析该函数在测试实例处的损失期望值，可以获得关于预测误差的重要知识。下面基于叠加模型，对回归预测函数进行计算，其结论对分类同样适用。

设某回归问题的理论预测函数为f(X)，用训练数据集Z拟合的实际预测函数为 ，其在统计总体上的损失期望值称为泛化误差（Generalization error），或测试误差（Test error），是监督学习模型理论上的评价指标：

在上式中，损失函数在输入和输出的联合概率分布上取期望值，由于 的参数是根据特定的训练数据集Z估算的，所以取给定Z下的条件期望。若再考虑训练数据集的随机性，计算泛化误差在Z所服从分布上的期望值，则得到泛化误差期望值或预测误差期望值：

即

                                                         

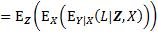
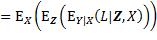
其中，最外层的期望算子针对输入的分布进行计算，内层的期望算子针对输出关于输入的条件分布和训练数据集的分布进行计算。考虑其内层期望在某测试输入x处的值，即该输入处的泛化误差期望值：

                                                                                          

因为训练数据集作为统计样本具有随机性，所以用不同训练数据集拟合的预测函数各异。即使输入确定为x，预测函数值 也是一个随机变量，随训练数据集的变化而波动。上式中的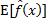 项就是针对训练数据集的分布取 的期望值。令

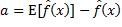
有：

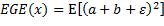
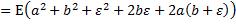
分析后两项：

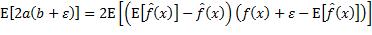
令c=E[fx] ，有：

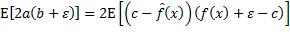
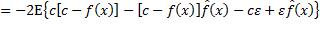
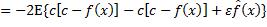
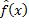的随机性来自训练数据集包含的实例，而ε的随机性来自测试实例，两个随机变量是相互独立的，从而有：

于是有：

综上可得：

之所以进行上述数学变换，是因为藉助最终呈现的形式，我们可以更好地理解用某个实际的预测函数所得的损失期望值。该值由三部分组成：第一部分是该预测函数的方差（Variance），代表由训练数据集的随机性导致的预测函数值的起伏；第二部分是理论预测函数值f(x)与实际预测函数值 的期望值之差——称为预测函数的偏差（Bias）——的平方，代表所用具体预测函数与理论预测函数之间的差距；第三部分则是理论预测函数都无法包含的输出噪声。实际预测函数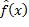 与理论预测函数f(x)有两点差异，一是用于训练 的数据集是一个样本而非统计总体，这导致了 值的波动性，即其方差；二是为了获得 ，采用了某种归纳偏好，这是 偏差[[1]]的来源。随机的实际输出值与确定的f(x)预测值之差则构成噪声：

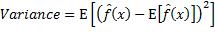
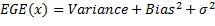
在三者中，由输出值的内在噪声ε贡献的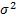 无法消除，偏差和方差则可以人为改变。有趣且吊诡的是，偏差和方差此消彼长。因此在采用具体的预测函数时，必须在两者之间做出权衡（Trade-off）。

 

---

[[1]] 在英文中偏好和偏差是同一个单词Bias。