python ---- 图像小波变换DWT

Posted 2023-04-07 星月夜语

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了python ---- 图像小波变换DWT相关的知识，希望对你有一定的参考价值。

数字图像中，离散小波变换在python中的使用

一、各种DWT小波变换含义

二、查看DWT参数

三、具体代码

一、各种DWT小波变换含义

python 的 pywt库中wavedec函数的wavelet参数取值:

'db1' ~ 'db45': Daubechies小波
'sym1' ~ 'sym20': Symlets小波
'coif1' ~ 'coif5': Coiflets小波
'bior1.1' ~ 'bior6.8': Biorthogonal小波
'rbio1.1' ~ 'rbio6.8': Reverse Biorthogonal小波
'meyr' : Meyer小波
'dmey': Discrete Meyer小波

二、查看DWT参数

python中：

print(pywt.wavelist(kind='discrete'))，打印出DWT类型：

['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']

三、具体代码

def full_Sparse(input, level, type='haar', height=0, width=0, threshold=0.8, DWT = True, slices=0):

    print(pywt.wavelist(kind='discrete'))
    shift_num = 0
    if DWT == True:
        input = (input-shift_num)
        N = height*width
      
        if type != "dct":
            coeffs2 = pywt.wavedec2(input, type, mode='periodization', level=level)  # 小波变换
            img_fre_full, slices = pywt.coeffs_to_array(coeffs2)  # 拼接成原图大小
        else:
            img_fre_full = cv2.dct(input.astype(dtype=np.float32))

        if threshold  < 1:
            img_fre = np.reshape(img_fre_full, (height*width), "F")
            sort_cof = np.sort(np.abs(img_fre), axis=0)
            threshold = int(np.ceil(threshold * N))
            thresh_val = sort_cof[N-threshold]
            img_fre_full[np.abs(img_fre_full) <= thresh_val] = 0.0

        return img_fre_full, slices
    else:  ## IDWT
        if type != "dct":
            coeffs_n = pywt.array_to_coeffs(input, slices, output_format='wavedec2')  # 将图片重新变成coeffs
            temp_im = pywt.waverec2(coeffs_n, type, mode='periodization')  # 反变换到像素域
      
        else:
            temp_im = cv2.idct(input)
        temp_im = temp_im  + shift_num
        return temp_im

图像隐写基于matlab小波变换DWT数字盲水印嵌入+攻击含Matlab源码 2313期

⛄一、离散小波变换的音频信号数字水印技术简介

0 引言
近年来, 数字水印技术的作用越来越重要。数字水印技术是将一些标识信息直接嵌入数字载体当中, 或间接表示在信号载体中, 且不影响原载体的使用价值。通过隐藏在载体中的这些信息, 可以判断信息是否被篡改, 具有防伪溯源、保护信息安全、版权保护等作用。对于广播转播台站而言, 是广播音频的中转站, 在广播信号发送至千家万户之前务必保证信号的安全可靠, 但现在的大部分台站只是利用人耳的判断, 以及不同信源之间的比较, 具有较大的局限性。若利用数字水印的特性, 应用于广播节目中可以有效地防止信号插播, 可靠地保护信号安全, 保障广播的安全播出。

1 音频数字水印技术分类
根据数字水印在音频信号中的处理技术, 可将数字水印分为时域、变换域、压缩域数字水印。

1.1 时域数字水印
在时域数字水印技术中, 直接将水印信息嵌入至音频信号中, 通常会选择隐藏在信号不重要部位, 以保证其嵌入水印不影响原音频信号的监听效果。时域水印技术的实现较为容易且运算量小, 简单直接, 但是鲁棒性差, 容易被破解, 抵抗力较差。

1.2 变换域数字水印
在变换域数字水印中, 音频信号需经过时域至变换域的转换, 通常的变换域有离散余弦变换 (DCT, Discrete Cosine Transform) 、离散傅立叶变换 (DFT, Discrete Fourier transform) 、离散小波变换 (DWT, Discrete Wavelet Transform) 等。在变换域中嵌入水印信息, 通过反变换得到嵌入水印的音频时域信号。变换域水印技术较时域水印技术复杂, 但变换域嵌入的水印信息较时域而言, 不可见性更强, 隐蔽性更好, 鲁棒性更好。本文的研究主要基于DWT的音频信号的水印信息的嵌入与提取。

1.3 压缩域数字水印
在时域和变换域的水印技术, 都是直接将水印信号嵌入未压缩的音频格式中, 但是通常在音频信号的传输或存储中需要对音频信号进行压缩编码 (例如WMA、MP3等) , 因此压缩域数字水印也是水印技术也具有较大的实用价值。压缩域数字水印技术大致可分为三类: (1) 在非压缩域嵌入水印, 将音频信号与水印信息一起压缩; (2) 在压缩域中, 直接将水印信息嵌入压缩的音频信号中; (3) 将压缩后的信号进行解压缩, 然后嵌入水印信息, 最后将水印信息和解压后的音频信号一起压缩。总的来说, 压缩域水印技术的编解码系统过于复杂, 受压缩编码格式限制大, 压缩后的音频信号已经去除了冗余, 因此加入水印的难度大, 压缩域水印技术有待进一步研究。

2 基于DWT的音频水印算法
2.1 水印嵌入
本文研究的音频水印算法是基于离散小波变换 (DWT) , 音频信号通过DWT变换, 在变换域中嵌入水印信息, 再经过逆变换 (IDWT) 从而得到嵌入水印的音频信号。水印嵌入原理框图如图1所示。

假定水印为M1×M2的二维图像bw, 由于音频信号通常为一维向量, 故水印信息在嵌入音频信号之前需要将二维降至一维向量w, 即M=M1×M2。通常我们也可以将图像进行打乱加密, 增强水印隐蔽性。

假定语音信号为s, 长度为N, 则s=s1, s2, s3, …, sN由于语音信号较长在处理中一般需要进行分段, 每段长度设为N1, 故该语音信号分为K=fix (N/N1) 段进行处理, 每段语音均嵌入一个水印信息。

小波变换是为了解决傅立叶变换的不足而提出的一种分析变换, 傅立叶变换的基函数是铺满整个时域的正弦信号, 对于突变信号以及变化的频率成分信息均不能较准确地表示。而小波变换是时间和频率的局部变换, 更能准确地表示音频信号的频域特征, 常用的小波基有Haar小波、Daubechies (db N) 小波、Marr小波等。本文采用的小波基是Haar小波, 它是支撑域在t∈[0, 1]范围内的矩形波, 定义如下:

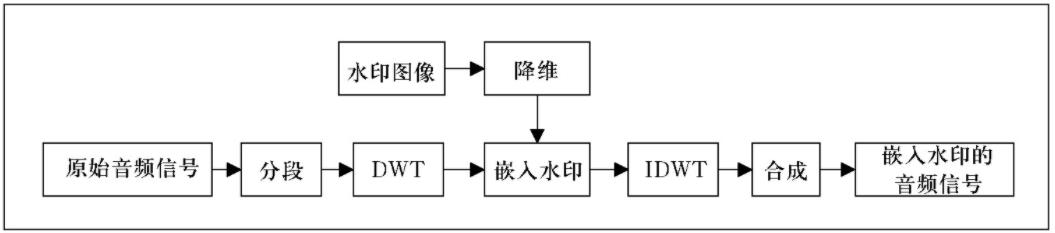
图1 音频信号水印嵌入原理框图

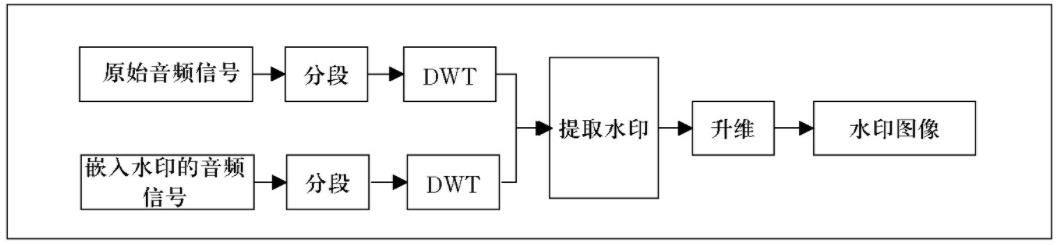
图2 音频信号水印提取原理框图

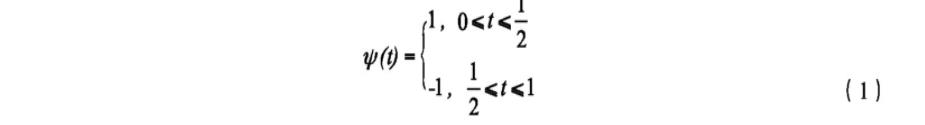
取定Haar小波基后, 则语音信号s可以表示为:

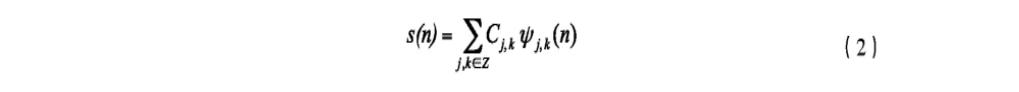
其中Cj, k为离散小波系数, 将音频信号分解为低频的近似部分和高频的细节部分, 我们在水印信息的嵌入处理中, 主要针对代表低频近似部分的系数向量处理, 即将水印信号放入低频近似部分, 高频细节部分不变, 以保证语音质量基本不变。由于嵌入的水印为二值图像, 因此如果水印信息的值为1, 则将对应的低频系数增大, 相反如果值为0, 则将对应的低频系数降低。在DWT域嵌入水印信息后, 然后通过IDWT变换, 将语音信号变换成时域信号。

2.2 水印提取
为了保证信息安全, 在发送端发送嵌入水印的音频信号, 而在接收端为了确定音频信息的准确性, 我们通常需要提取水印以确保来源的真实性, 因此水印的提取技术也尤为重要。在水印提取过程中, 需要原始音频信号与嵌入水印的音频信号同时进行DWT, 再将两者参数进行分析比较提取出水印信息。水印提取原理框图如图2所示。

在前面所述的水印嵌入过程中, 将水印信息嵌入高频的细节部分, 因此在提取水印过程中, 我们也只需比较原始语音信号S的低频小波系数向量c A与嵌入水印的音频信号s1的低频小波系数向量c A1作比较, 若c A1>c A, 则水印信息为1;反之则为0, 再通过向量平均, 如此得到水印信息的一维向量, 最后通过升维得到二值图像。

⛄二、部分源代码

clc
clear

im=imread(‘lena.bmp’);
imorig=im2double(im);
imwm=imread(‘watermark.jpg’);
imwm=im2bw(imwm,0.5);
imwtwm=wmembed(imorig,imwm,0.2);

figure(1), imshow(imorig);
title(‘原始图片’);
figure(2), imshow(imwm);
title(‘水印图片’);
figure(3), imshow(imwtwm);
title(‘含嵌入水印图片’);
imwrite(imwtwm,‘watermarked image.jpg’);

wmext = wmextract(imwtwm,0.2,2);
figure(4), imshow(wmext);
title(‘extracted Watermark’);

%%%%%%攻击实验测试鲁棒性%%%%%%%
%1 添加白噪声;
%2 高斯低通滤波;
%3 JPEG 压缩;
%4 图像剪切;
%5 旋转90度;
%6 直接检测水印;

figure(5)

    image1=imwtwm;                    %添加白噪声
    noise=0.02*randn(size(image1));
    image1=image1 + noise;
    M1=image1;

    image2=imwtwm;                    %高斯低通滤波
    H=fspecial('gaussian',[4,4],0.2);
    image2=imfilter(image2,H);
    M2=image2;

    image3=imread('watermarked image.jpg'); %JPEG 压缩
    M3=image3;

    image4=imwtwm;                    %图像剪切
    image4(1:128,1:128)=256;
    M4=image4;

    image5=imwtwm;                    %旋转90度
    image5=imrotate(image5,90,'crop');
    image5=mat2gray(image5);
    M5=image5;
    
    M6=imwtwm;                        %直接检测水印

subplot(2,3,1),
imshow(imwtwm),title(‘未受攻击含水印图像’);
subplot(2,3,2),
imshow(image1),title(‘加入高斯白噪声’);
subplot(2,3,3),
imshow(image2),title(‘高斯低通滤波’);
subplot(2,3,4),
imshow(image3,[]),title(‘JPEG 压缩’);
subplot(2,3,5),
imshow(image4),title(‘部分剪切’);
subplot(2,3,6),
imshow(image5),title(‘旋转90度’);

%%%%%%%%%攻击后提取水印%%%%%%%%%
figure(6),

    wmext1 = wmextract(imwtwm,0.2,2);
    wmext2 = wmextract(image1,0.2,2);
    wmext3 = wmextract(image2,0.2,2);
    wmext4 = wmextract(image3,0.2,2);
    wmext5 = wmextract(image4,0.2,2);
    wmext6 = wmextract(image5,0.2,2);

subplot(2,3,1),
imshow(wmext1),title(‘直接提取水印’);
subplot(2,3,2),
imshow(wmext2),title(‘加入高斯白噪声提取水印’);
subplot(2,3,3),
imshow(wmext3),title(‘高斯低通滤波提取水印’);
subplot(2,3,4),
imshow(wmext4),title(‘JPEG压缩提取水印’);
subplot(2,3,5),
imshow(wmext5),title(‘部分剪切提取水印’);
subplot(2,3,6),
imshow(wmext6),title(‘旋转90度提取水印’);