2DWT：2维离散小波变换（附Pytorch代码）

Posted 2022-10-07 NorthSmile

二维离散小波变换

• 一、相关基础
• • 1.小波变换基础函数
  • 2.小波变换
• 二、原理
• 三、基本小波基：哈尔小波
• 四、代码实现
• 参考：

图像信号具有非平稳特性，无法使用一种确定的数学模型来描述，而小波变换的多分辨率分析特性很好地解决了这个问题。小波变化的多分辨率特性使其既可以高效描述图像的平坦区域（低频信息、全局信息），也可以有效处理图像信号的局部突变（高频信息，即图像的边缘轮廓等部分）。小波变换在空域和频域同时具有良好的局部性，使其可以很好地聚焦到图像的任意细节。

一、相关基础

1.小波变换基础函数

二维小波变换的基础函数为：

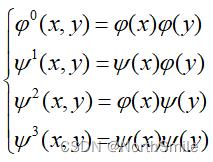
其中φ(x,y)为一个可分离二维尺度函数，φ(x)为一维尺度函数；ψ¹(x,y)、ψ²(x,y)、ψ³(x,y)均为“方向敏感”可分离二维小波函数，且分别表示沿着列的水平方向、行的垂直方向以及对角线方向边缘的灰度变化 ，ψ(x)为一维小波函数。对一维离散小波变换进行推广即可得到二维离散小波变换。

2.小波变换

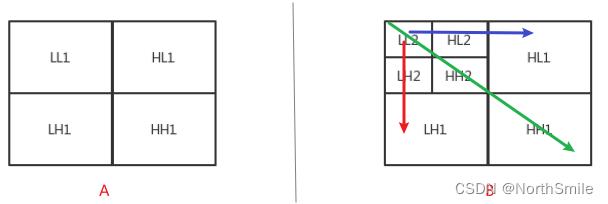
对图像每进行一次小波变换，会分解产生一个低频子带（LL：行低频、列低频）和三个高频子带(垂直子带LH：行低频、列高频；水平子带HL：行高频、列低频；对角子带HH：行高频、列高频），后续小波变换基于上一级低频子带LL进行，依次重复，可完成对图像的i级小波变换，其中i=(1,2,3,…I）。A图、B图分别为i=1时的一级小波变换分布，i=2时的二级小波变换分布，每个子带分别包含各自对应的小波系数。可以看到，其实每次小波变换可以看做对图像的行水平方向、列垂直方向分别进行隔点采样，如此空间分辨率每次变为1/2，因此第i级小波变换后，其子带空间分辨率为原图的1/2ⁱ。

二、原理

利用二维Mallat算法，采用可分离的滤波器进行小波变换，实质上是利用一维滤波器分别对图像数据的行和列进行一维小波变换。
小波分解实现原理如下：
原图利用一维滤波器先进行行滤波得到L1、H1；然后进行列滤波得到四个子带LL1、LH1、HL1、HH1。

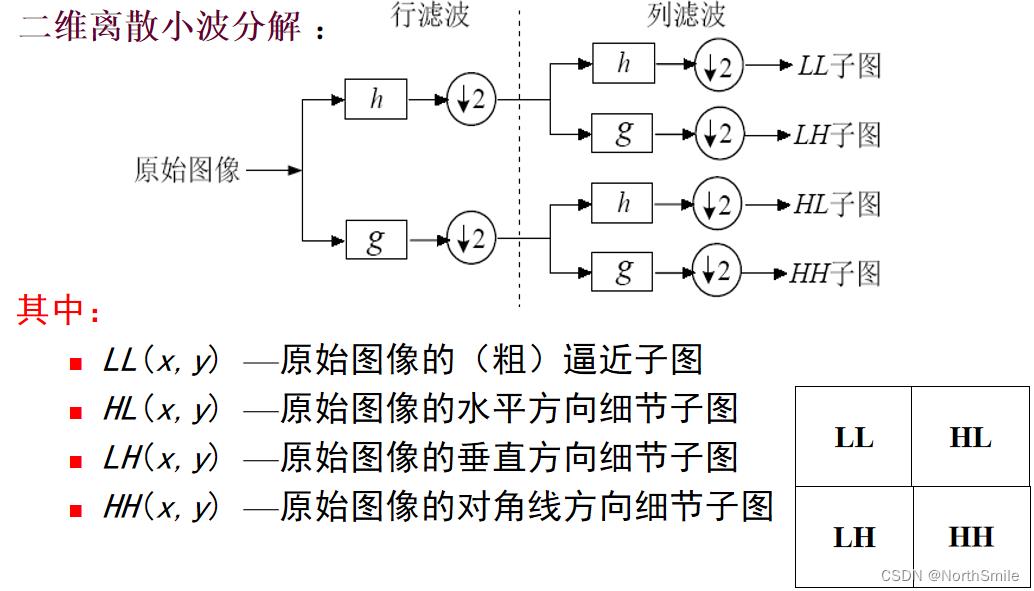
小波变换是可逆的，进行小波分解得到的子图可通过组合重构原图，其实现原理如下：

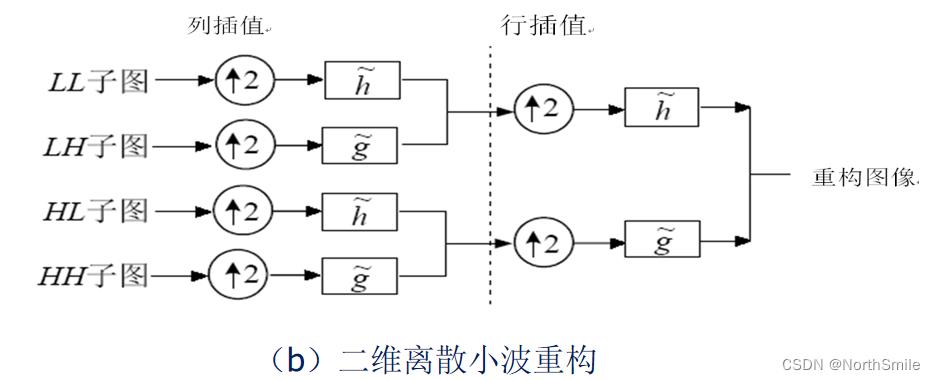
1.举个例子

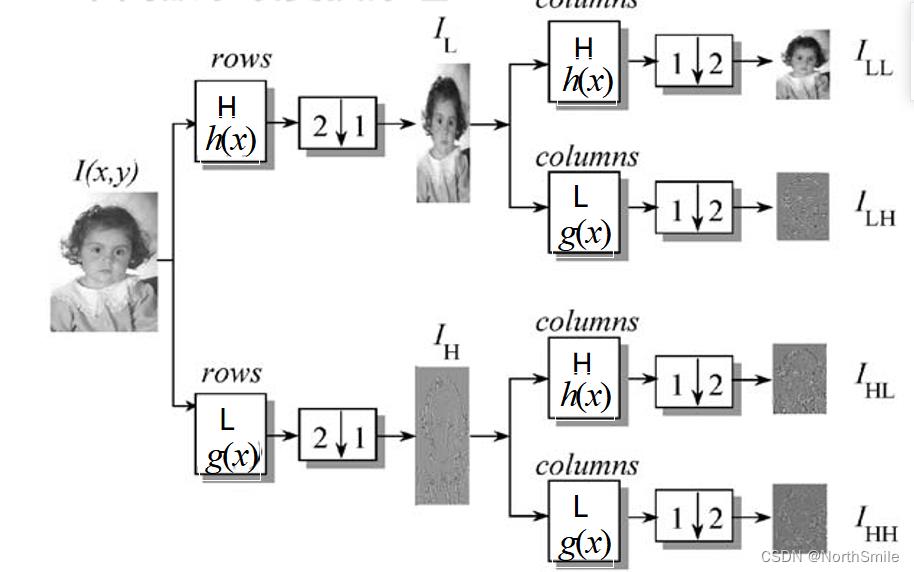
假设输入图像I大小为M×N，且M=2^m、N=2ⁿ，对其进行一级小波分解过程如下：
（1）利用一维滤波器h和g分别对输入图像I进行行滤波，丢弃奇数行，得到大小为M/2×N的中间输出I_L和I_H；
（2）一维滤波器h和g分别对中间输出I_L和I_H进行列滤波，丢弃奇数列，得到大小为M/2×N/2的分解输出I_LL、I_LH和I_HL、I_HH；

三、基本小波基：哈尔小波

哈尔（Haar）小波是最常用的小波基，公式定义如下：

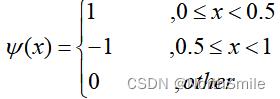
其对应的尺度函数为：

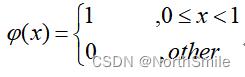
哈尔小波具有最短的支集，支集长度为1，滤波器长度为2，具有正交性和对称性，其图示如下：

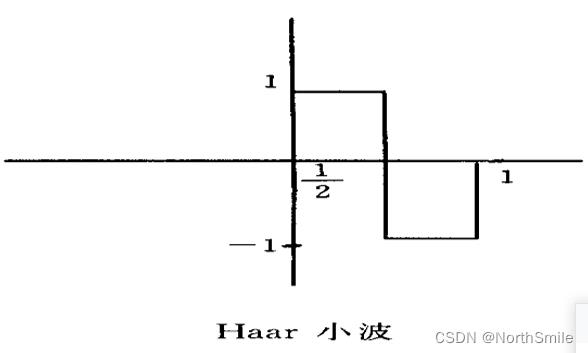
1.举例说明
对于一维哈尔小波变换来说，其一维高通滤波器F_H=[1,-1]、一维低通滤波器F_L=[1,1]，假设输入向量X[6]=[2,4,6,8,5,9]，对其进行一维哈尔小波变换过程如下（图中蓝色填充表示滤波器的移动过程，黄色表示输入数据，绿色表示对应输出）：
1）高通滤波，求相邻元素之间差值的平均值，存储输入数据的细节信息：
比如输出中的第一个元素为-1=(1×2-1×4)/2

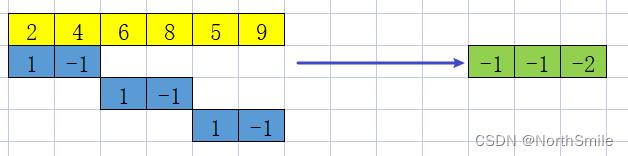
2）低通滤波，求相邻元素的平均值，存储输入数据的粗略近似信息：
比如输出中的第一个元素为3=(1×2+1×4)/2

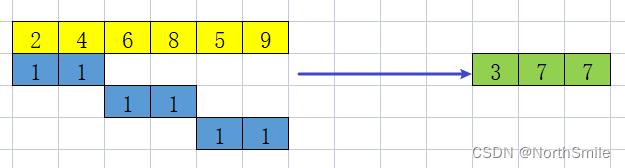
前面提到，二维变换只不过是将输入的二维数据依次进行行滤波和列滤波（其实先行后列或者先列后行不影响），在此过程中行滤波和列滤波均进行一维小波变换，假设输入图像大小为M×N：

• 行滤波分别采用一维高通滤波器、一维低通滤波器得到对应的两个输出，输出大小均为M/2×N；
• 列滤波对于行滤波的两个输出，同样采用一维高通滤波器、一维低通滤波器得到对应的四个输出，输出大小均为M/2×N/2；

将一维哈尔小波变换推广，进一步可得到二维哈尔小波变换的实现过程，对应的四个滤波器分别为：

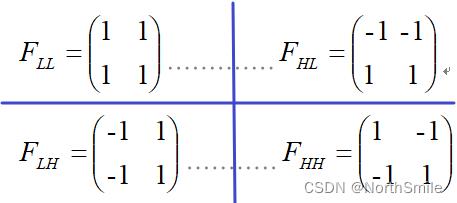
假设输入如下图HR，左上角ABCD四个元素构成一个局部区域，依次使用上述四个滤波器对该局部区域进行计算即可得到小波分解后对应子带中的一个元素，依次类推，计算公式如下：

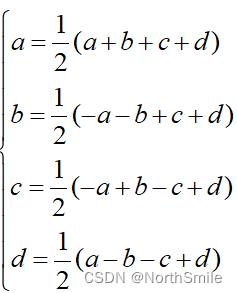
四、代码实现

def dwt_init(x):
    x01 = x[:, :, 0::2, :] / 2
    x02 = x[:, :, 1::2, :] / 2
    x1 = x01[:, :, :, 0::2]
    x2 = x02[:, :, :, 0::2]
    x3 = x01[:, :, :, 1::2]
    x4 = x02[:, :, :, 1::2]
    x_LL = x1 + x2 + x3 + x4
    x_HL = -x1 - x2 + x3 + x4
    x_LH = -x1 + x2 - x3 + x4
    x_HH = x1 - x2 - x3 + x4

    return torch.cat((x_LL, x_HL, x_LH, x_HH), 1)


def iwt_init(x):
    r = 2
    in_batch, in_channel, in_height, in_width = x.size()
    # print([in_batch, in_channel, in_height, in_width])
    out_batch, out_channel, out_height, out_width = in_batch, int(
        in_channel / (r ** 2)), r * in_height, r * in_width
    x1 = x[:, 0:out_channel, :, :] / 2
    x2 = x[:, out_channel:out_channel * 2, :, :] / 2
    x3 = x[:, out_channel * 2:out_channel * 3, :, :] / 2
    x4 = x[:, out_channel * 3:out_channel * 4, :, :] / 2

    h = torch.zeros([out_batch, out_channel, out_height, out_width]).float().cuda()

    h[:, :, 0::2, 0::2] = x1 - x2 - x3 + x4
    h[:, :, 1::2, 0::2] = x1 - x2 + x3 - x4
    h[:, :, 0::2, 1::2] = x1 + x2 - x3 - x4
    h[:, :, 1::2, 1::2] = x1 + x2 + x3 + x4

    return h


class DWT(nn.Module):
    def __init__(self):
        super(DWT, self).__init__()
        self.requires_grad = False

    def forward(self, x):
        return dwt_init(x)


class IWT(nn.Module):
    def __init__(self):
        super(IWT, self).__init__()
        self.requires_grad = False

    def forward(self, x):
        return iwt_init(x)

1.测试案例

dwt_module=DWT()
x=Image.open('./iu.png')
# x=Image.open('./mountain.png')
x=transforms.ToTensor()(x)
x=torch.unsqueeze(x,0)
x=transforms.Resize(size=(256,256))(x)
subbands=dwt_module(x)

title=['LL','HL','LH','HH']

plt.figure()
for i in range(4):
    plt.subplot(2,2,i+1)
    temp=torch.permute(subbands[0,3*i:3*(i+1),:,:],dims=[1,2,0])
    plt.imshow(temp)
    plt.title(title[i])
    plt.axis('off')
plt.show()

参考：

（1）《数字图像处理》，作者李俊山等。
（2）https://github.com/lpj-github-io/MWCNNv2/blob/master/MWCNN_code/model/common.py