逻辑回归和SVM的区别是啥？各适用于解决啥问题

Posted 2023-04-04

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了逻辑回归和SVM的区别是啥？各适用于解决啥问题相关的知识，希望对你有一定的参考价值。

两种方法都是常见的分类算法,从目标函数来看,区别在于逻辑回归采用的是logistical loss,svm采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重.SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器.而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重.两者的根本目的都是一样的.此外,根据需要,两个方法都可以增加不同的正则化项,如l1,l2等等.所以在很多实验中,两种算法的结果是很接近的.
但是逻辑回归相对来说模型更简单,好理解,实现起来,特别是大规模线性分类时比较方便.而SVM的理解和优化相对来说复杂一些.但是SVM的理论基础更加牢固,有一套结构化风险最小化的理论基础,虽然一般使用的人不太会去关注.还有很重要的一点,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算
svm 更多的属于非参数模型,而logistic regression 是参数模型,本质不同.其区别就可以参考参数模型和非参模型的区别就好了.
logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了参考技术A 这两种算法都是常见的分类算法，如果从目标函数来说，区别在于logistic回归采用的是log对数损失函数L(Y,P(Y|X))=-log(P(Y|X))，SVM采用的是hingle loss.损失函数的目的都是增加对分类影响较大的数据点的权重，减小对分类影响小的数据点的权重。
SVM只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而logistic回归通过非线性映射，大大减小离分类平面较远地点的权重，相对提升与分类最相关的数据点的权重。
在工业实际应用中，SVM用的不多，速度慢而且效果很难保证。
在Andrew Ng的机器学习视频中提到SVM和logistic回归的适用情形：
m是样本数，n是特征的数目
1、如果n相对于m来说很大，则使用logistic回归或者不带核函数的SVM（线性分类）
2、如果n很小，m的数量适中（n=1-1000，m=10-10000），使用带核函数的SVM算法
3、如果n很小，m很大（n=1-1000,m=50000+）,增加更多的特征，然后使用logistic回归或者不带核函数的SVM。参考技术B 神经网络的设计要用到遗传算法，遗传算法在神经网络中的应用主要反映在3个方面：网络的学习，网络的结构设计，网络的分析。
1．遗传算法在网络学习中的应用
在神经网络中，遗传算法可用于网络的学习。这时，它在两个方面起作用
(1)学习规则的优化
用遗传算法对神经网络学习规则实现自动优化，从而提高学习速率。
(2)网络权系数的优化
用遗传算法的全局优化及隐含并行性的特点提高权系数优化速度。
2．遗传算法在网络设计中的应用
用遗传算法设计一个优秀的神经网络结构，首先是要解决网络结构的编码问题；然后才能以选择、交叉、变异操作得出最优结构。编码方法主要有下列3种：
(1)直接编码法
这是把神经网络结构直接用二进制串表示，在遗传算法中，“染色体”实质上和神经网络是一种映射关系。通过对“染色体”的优化就实现了对网络的优化。
(2)参数化编码法
参数化编码采用的编码较为抽象，编码包括网络层数、每层神经元数、各层互连方式等信息。一般对进化后的优化“染色体”进行分析，然后产生网络的结构。
(3)繁衍生长法
这种方法不是在“染色体”中直接编码神经网络的结构，而是把一些简单的生长语法规则编码入“染色体”中；然后，由遗传算法对这些生长语法规则不断进行改变，最后生成适合所解的问题的神经网络。这种方法与自然界生物地生长进化相一致。
3．遗传算法在网络分析中的应用
遗传算法可用于分析神经网络。神经网络由于有分布存储等特点，一般难以从其拓扑结构直接理解其功能。遗传算法可对神经网络进行功能分析，性质分析，状态分析。
遗传算法虽然可以在多种领域都有实际应用，并且也展示了它潜力和宽广前景；但是，遗传算法还有大量的问题需要研究，目前也还有各种不足。首先，在变量多，取值范围大或无给定范围时，收敛速度下降；其次，可找到最优解附近，但无法精确确定最扰解位置；最后，遗传算法的参数选择尚未有定量方法。对遗传算法，还需要进一步研究其数学基础理论；还需要在理论上证明它与其它优化技术的优劣及原因；还需研究硬件化的遗传算法；以及遗传算法的通用编程和形式等。

机器学习—逻辑回归与SVM区别

逻辑回归详细推导：http://lib.csdn.net/article/machinelearning/35119

面试常见问题：https://www.cnblogs.com/ModifyRong/p/7739955.html

1、LR和SVM有什么相同点

　　（1）都是监督分类算法，判别模型；

　　（2）LR和SVM都可以处理分类问题，且一般都用于处理线性二分类问题（在改进的情况下可以处理多分类问题）；

　　（3）两个方法都可以增加不同的正则化项，如L1、L2等等。所以在很多实验中，两种算法的结果是很接近的。

2、LR和SVM有什么不同点

　　（1）本质上是其loss function不同；

　　区别在于逻辑回归采用的是Logistical Loss，SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。

　　逻辑回归损失函数：

　　SVM损失函数：

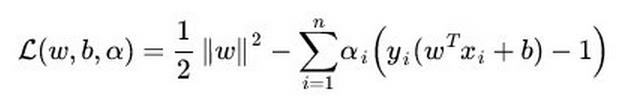
　　LR方法基于概率理论，假设样本为0或者1的概率可以用sigmoid函数来表示，然后通过极大似然估计的方法估计出参数的值，或者从信息论的角度来看，其是让模型产生的分布 $P (Y | X)$

　　（2）SVM只考虑分类面上的点，而LR考虑所有点（远离的点对边界线的确定也起作用）

　　SVM中，在支持向量之外添加减少任何点都对结果没有影响，而LR则是每一个点都会影响决策。
　　Linear SVM不直接依赖于数据分布，分类平面不受一类点影响；LR则是受所有数据点的影响，所以受数据本身分布影响的，如果数据不同类别strongly unbalance，一般需要先对数据做balancing。

　　（3）在解决非线性问题时，支持向量机采用核函数的机制，而LR通常不采用核函数的方法。

　　SVM转化为对偶问题后，分类只需要计算与少数几个支持向量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算量。而LR则每个点都需要两两计算核函数，计算量太过庞大。

　　（4）SVM依赖于数据的测度，而LR则不受影响

　　因为SVM是基于距离的，而LR是基于概率的，所以LR是不受数据不同维度测度不同的影响，而SVM因为要最小化 $\frac{1}{2} | | w | |^{2}$

$\frac{1}{2} | | w | |^{2}$

　　（5）SVM自带结构风险最小化，LR则是经验风险最小化

　　SVM的损失函数就自带正则！！！（损失函数中的1/2||w||^2项），这就是为什么SVM是结构风险最小化算法的原因！！！而LR必须另外在损失函数上添加正则项！！！

　　以前一直不理解为什么SVM叫做结构风险最小化算法，所谓结构风险最小化，意思就是在训练误差和模型复杂度之间寻求平衡，防止过拟合，从而达到真实误差的最小化。来达到结构风险最小化的目的，最常用的方法就是添加正则项，而SVM自带正则项。

　　（6）LR和SVM在实际应用的区别

　　根据经验来看，对于小规模数据集，SVM的效果要好于LR，但是大数据中，SVM的计算复杂度受到限制，而LR因为训练简单，可以在线训练，所以经常会被大量采用【听今日头条的同学说，他们用LR用的就非常的多】

转自：简书作者

以上是关于逻辑回归和SVM的区别是啥？各适用于解决啥问题的主要内容，如果未能解决你的问题，请参考以下文章