损失函数(lossfunction)的全面介绍(简单易懂版)
Posted 小林学编程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了损失函数(lossfunction)的全面介绍(简单易懂版)相关的知识,希望对你有一定的参考价值。
一:什么是损失函数:
简单的理解就是每一个样本经过模型后会得到一个预测值,然后得到的预测值和真实值的差值就成为损失(当然损失值越小证明模型越是成功),我们知道有许多不同种类的损失函数,这些函数本质上就是计算预测值和真实值的差距的一类型函数,然后经过库(如pytorch,tensorflow等)的封装形成了有具体名字的函数。
二:为什么需要损失函数:
我们上文说到损失函数是计算预测值和真实值的一类函数,而在机器学习中,我们想让预测值无限接近于真实值,所以需要将差值降到最低(在这个过程中就需要引入损失函数)。而在此过程中损失函数的选择是十分关键的,在具体的项目中,有些损失函数计算的差值梯度下降的快,而有些下降的慢,所以选择合适的损失函数也是十分关键的。
三:损失函数通常使用的位置:
在机器学习中,我们知道输入的feature(或称为x)需要通过模型(model)预测出y,此过程称为向前传播(forward pass),而要将预测与真实值的差值减小需要更新模型中的参数,这个过程称为向后传播(backward pass),其中我们损失函数(lossfunction)就基于这两种传播之间,起到一种有点像承上启下的作用,承上指:接収模型的预测值,启下指:计算预测值和真实值的差值,为下面反向传播提供输入数据。
四:常用的损失函数(基于pytorch):
1:L1Loss函数:
(1):数学本质:
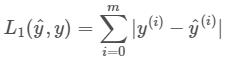
ps:1:带小帽子的y(y_hat)表示的是经过模型的预测值,y可以表示真实值。
2:图中的m指的是一行数据中的m列(下面证明中展现的更加清晰)
(2):证明:
我们首先先引用一下函数先计算一个结果:
import torch as th
import torch.nn as nn
loss=nn.L1Loss()
input=th.Tensor([2,3,4,5])
target=th.Tensor([4,5,6,7])
output=loss(input,target)
output
tensor(2.)
我们可以用手动计算来验证数学本质正不正确(数学本质中的m在文中具体数值为4):
output=(|2-4|+|3-5|+|4-6|+|5-7|)/4=2
ps:因为我们函数的“reduction”(l1loss函数的参数)选择的是默认的"mean"(平均值),所以还会在除以一个"4",如果我们设置“loss=L1Loss(reduction='sum')则不用再除以4。
2:MSELoss函数:
(1):数学本质:
ps:在此数学公式中的参数含义与L1Loss函数参数意义相同
(2):证明:
我们首先先引用一下函数先计算一个结果:
import torch as th
import torch.nn as nn
loss=nn.MSELoss()
input=th.Tensor([2,3,4,5])
target=th.Tensor([4,5,6,7])
output=loss(input,target)
output
tensor(4.)
我们可以用手动计算来验证数学本质正不正确:
output=[(2-4)^2+(3-5)^2+(4-6)^2+(5-7)^2 ]/4=4
3:CrossEntropyLoss函数(交叉熵函数)
因为此函数涉及到的知识内容很多,此文就不介绍此函数,在下文参考链接中我会提供详细描述此函数的文章,以供大家参考。
在读文章之前,先补充几个知识点,以便读者更好地看懂文章:
(1):CrossEntropyLoss函数主要用于分类项目中运用
(2) :one-hot(独热)编码:
| 猫 | 狗 | 兔 | |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
ps:最左边的一列1,2,3代表样本属于猫,狗,兔中的某一种,最上面一行是分类(图中猫,狗,兔三类属于三分类问题,当然在编码过程中种类是用数字来代替的),如图,1这一行在猫下有1(表示属于猫),在狗和兔下为0(表示1样本不属于狗和兔)以此类推,分类数据这样编写让样本与样本的欧式距离一致(根据离散特征的某个取值对应欧式空间的某一点)
(3)函数的理解: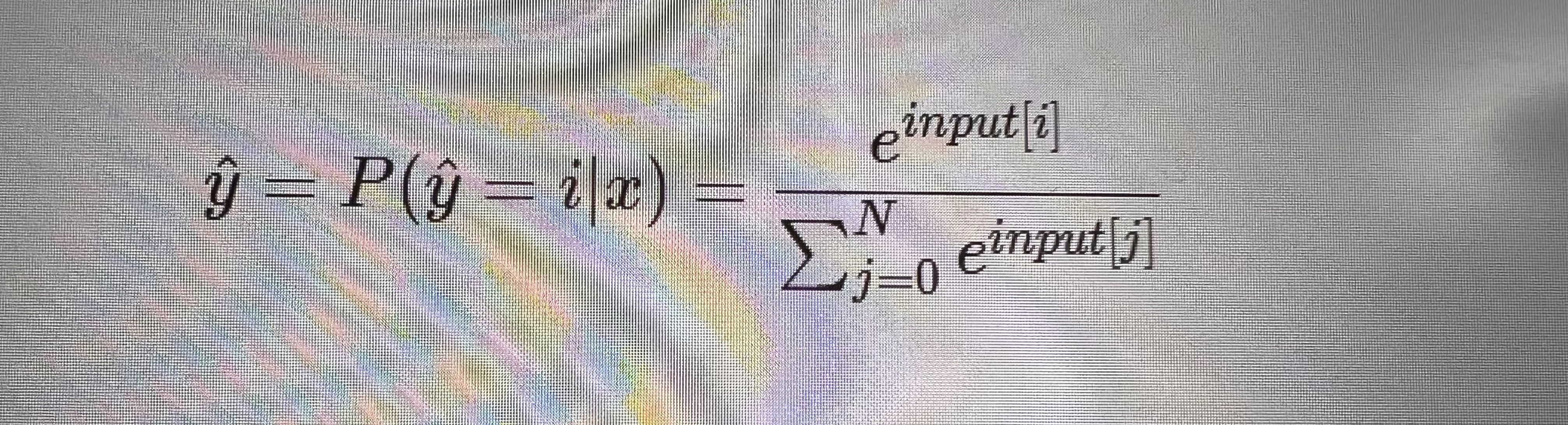
关于图中公式的理解,此变换是softmax函数变换具体表达方式如下:
假设输入的y_hat=[1,2,3,4]
则经过图中函数变换输出的值=[e^1/(e^1+e^2+e^3+e^4),e^2/(e^1+e^2+e^3+e^4),e^3/(e^1+e^2+e^3+e^4),e^4/(e^1+e^2+e^3+e^4)]
五:参考资料:
(1):CrossEntropyLoss函数的详细介绍:
https://blog.csdn.net/weixin_41940752/article/details/93159710
(2):其他损失函数:
https://blog.csdn.net/weixin_41122036/article/details/103270152
(3):CrossEntropyLoss函数怎么得来的:
logistic损失函数的解释
logistic回归的 P(y|x):预期输出为y时,输入为x的概率为p(y|x)=y~^y(1-y~)^(1-y)-------全面概括y=0|1的情况
loss function()= - log(p(y|x)); 可以根据loss function定义得到结果。
J(w,b)=-1/m求和loss--->求它的最小值用最大似然估计模型时,可以去掉符号。来进行估计
以上是关于损失函数(lossfunction)的全面介绍(简单易懂版)的主要内容,如果未能解决你的问题,请参考以下文章
论文笔记:A Comprehensive Survey of Regression Based LossFunctions for Time Series Forecasting