论文笔记：A Comprehensive Survey of Regression Based LossFunctions for Time Series Forecasting

Posted 2023-03-05 UQI-LIUWJ

比较了多种可用于时间序列的损失函数

1 损失函数逐个分析

1.1 Mean Absolute Error (MAE)

1.1.1 介绍

绝对误差均值

 1.1.2 图像

假定ground-truth是0，MAE和prediction的图像为：

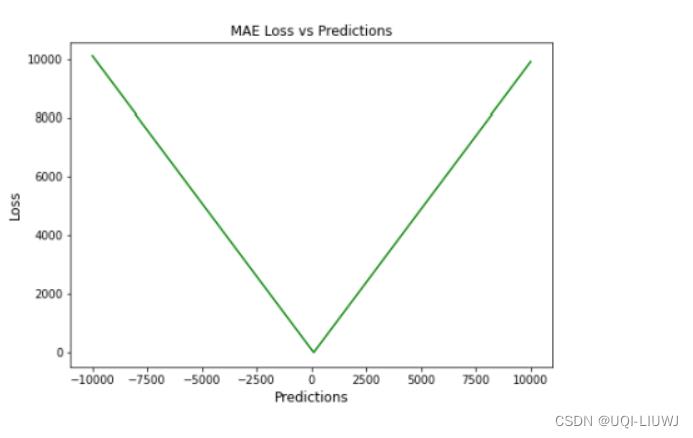
 1.1.3 优缺点

优点

• 计算简单
• 对异常值不太敏感

缺点

• 当prediction接近ground-truth的时候，梯度并没有下降——>可能在反向传播过程中跳过最小值
• 在零处不可微——>计算梯度很困难

1.2 Mean Squared Error (MSE)

1.2.1 介绍

均方误差

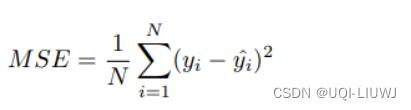
 1.2.2 图像

假定ground-truth是0，MSE和prediction的图像为

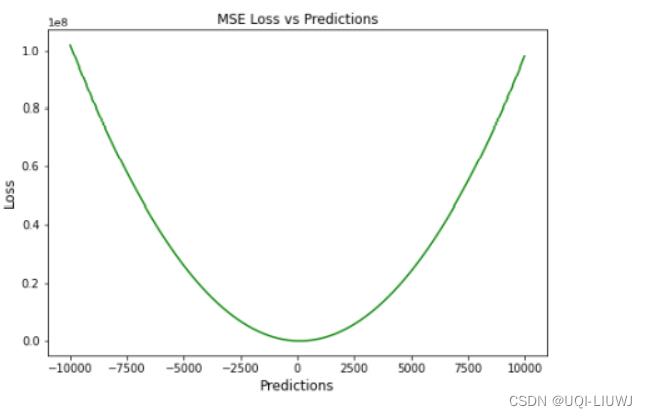
 1.2.3 优缺点

优点

• 当prediction接近ground-truth的时候，梯度逐渐减少——>有助于收敛到最小值

缺点

• 较大的损失值可能会导致梯度下降时步子过大
• 对异常值敏感——>显著异常值可能会影响性能

1.3 MBE

1.3.1 介绍

平均偏差误差

正偏差表示被高估，而负偏差表示被低估

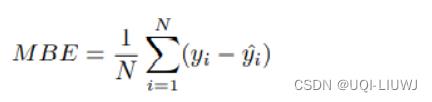
 1.3.2 图像

假定ground-truth是0

1.3.3 优缺点

优点

• 可以使用MBE确定模型的改进方向（估计高了还是低了）

缺点

• 误差往往会相互抵消，不是一个合适的损失函数

1.4 Relative Absolute Error (RAE)

1.4.1 介绍

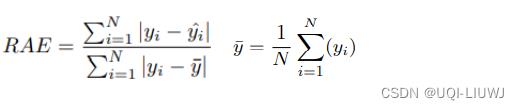
1.4.2 图像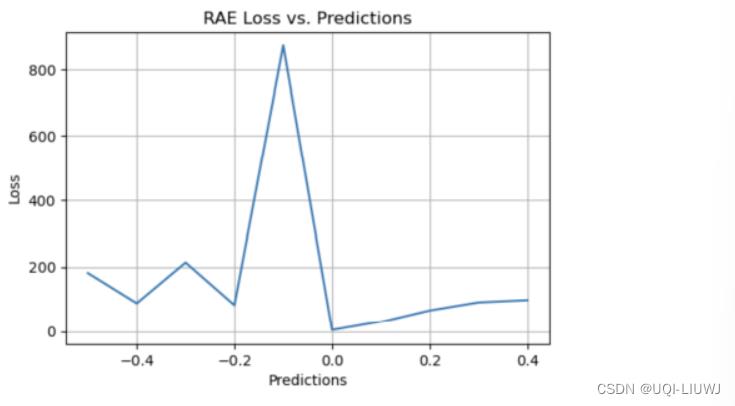

 1.4.3 优缺点

优点

• 可以比较以不同单位测量误差的模型
   

缺点

•  如果平均预测等于ground-truth，那么无法计算RAE

1.5 Relative Squared Error (RSE)

1.5.1 介绍  

1.5.2  图像

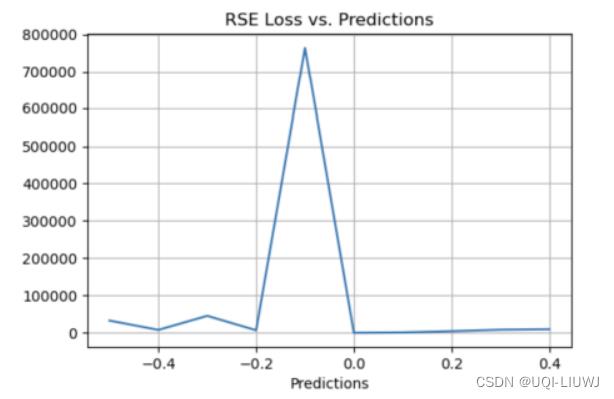
1.5.3 优缺点

优点

• 可以比较以不同单位测量误差的模型
   

缺点

•  如果平均预测等于ground-truth，那么无法计算RAE

1.6 Mean Relative Percentage Error (MAPE)

1.6.1 介绍 

平均绝对百分比误差 (MAPE)

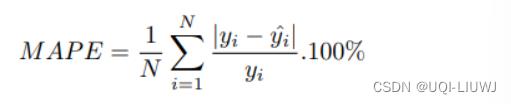
1.6.2 图像

（0这个位置应该没有定义，被挖掉）

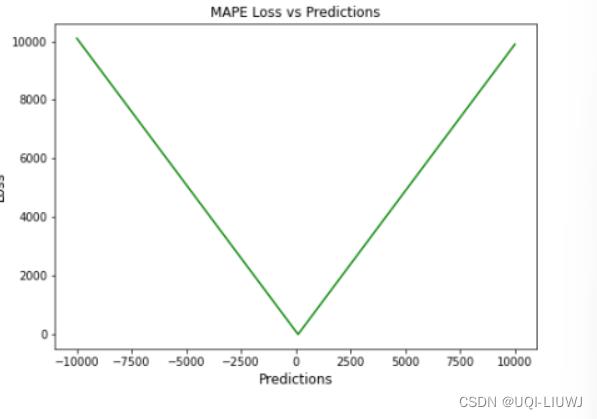
 1.6.3 优缺点

优点

• 与变量的规模无关
• 避免正数抵消负数的问题

缺点

• 分母可能是零——>导致未定义的值
• 正Loss的惩罚小于负Loss（一个是小一点的正数，另一个直接是负数）——>导致训练时有一定的偏差

1.7 Root Mean Squared Error (RMSE)

1.7.1 介绍 

均方根偏差

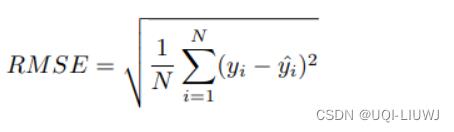
1.7.2 图像

1.7.3 优缺点

优点

• 对于极端异常值来说，平方根的限制导致RMSE的惩罚小于MSE，梯度不会下降得太快

缺点

• RMSE仍然是一个线性平分函数，所以当prediction接近ground-truth的时候，梯度也并没有下降——>也有可能在反向传播过程中跳过最小值
• 在零处不可微——>计算梯度很困难

 1.8 MSLE

1.8.1 介绍

均方对数误差 (MSLE) 

通过对数减少对实际值和预测值之间的百分比差异以及两者之间的相对差异

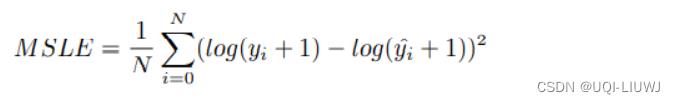
 1.8.2 图像

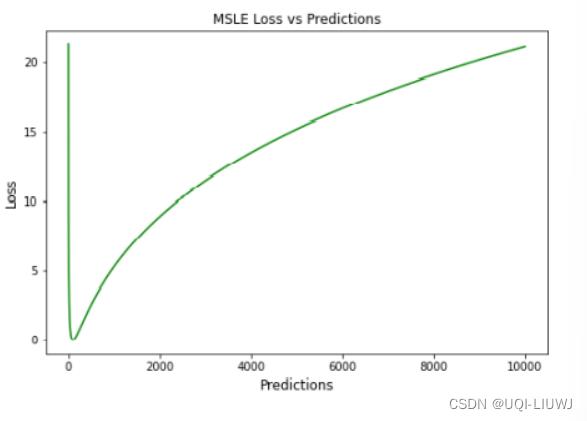
 1.8.3 优缺点

优点

• 将实际值和预测值之间的小差异和大差异进行粗略处理

缺点

• 对不充分的预测的惩罚比对过度预测的惩罚更多（低估比高估受到更严重的惩罚）

1.9 Root Mean Squared Logarithmic Error (RMSLE)

1.9.1 介绍

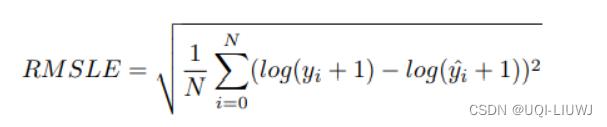
 1.9.2 图像

1.9.3 优缺点

优点

• 将实际值和预测值之间的小差异和大差异进行粗略处理

缺点

• 对不充分的预测的惩罚比对过度预测的惩罚更多（低估比高估受到更严重的惩罚）

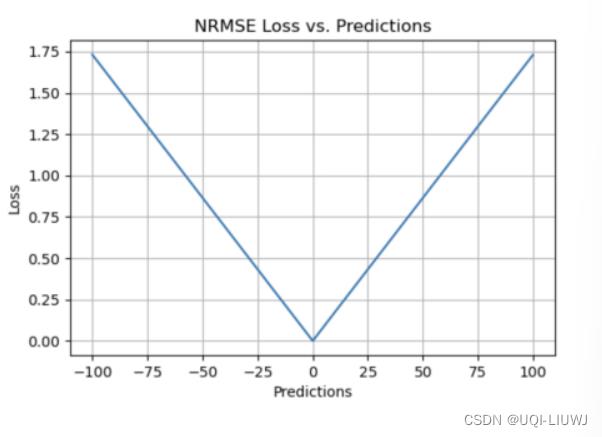
1.10 Normalized Root Mean Squared Error (NRMSE)

1.10.1 介绍

将 RMSE 观测范围归一化

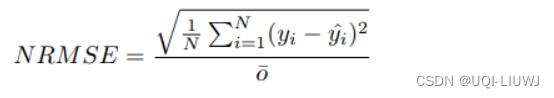
o是观测值的平均值

1.10.2 图像

 

 1.10.3 优缺点

优点

• 不同尺度或数据集模型之间的比较 较为容易

缺点

• 无法响应变量相关的单位

1.11 Relative Root Mean Squared Error (RRMSE)

 

 

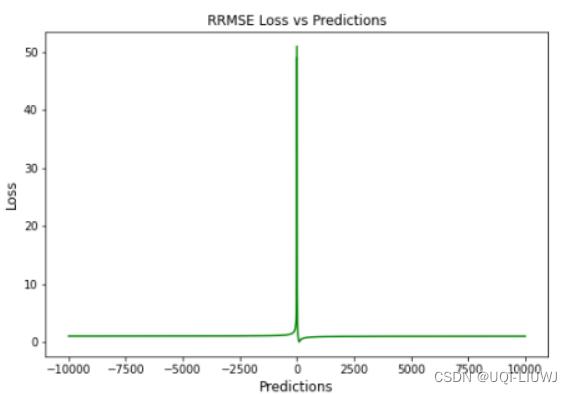
1.12 Huber Loss

1.12.1 介绍

二次和线性平分方法的理想组合：对于小于 δ 的损失值，应该使用 MSE；对于大于 δ 的损失值，应使用 MAE

1.12.2  图像

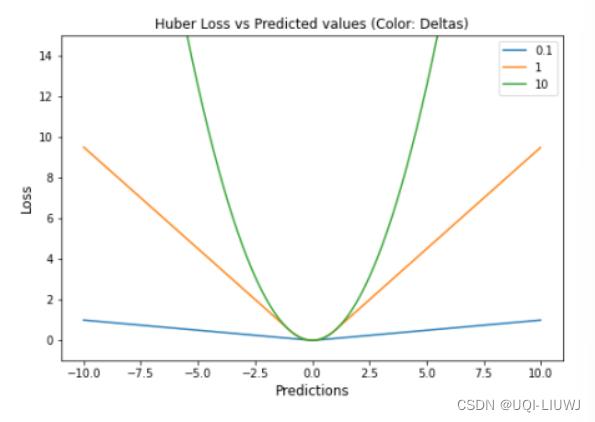
1.12.3 优缺点 

优点：

• 超参数δ以上的线性保证了异常值被赋予适当的权重，不像MSE中那样极端
• 超参数δ以下的弯曲形状保证了在反向传播过程中梯度长是正确的。

缺点

• 由于额外的条件和比较，Huber Loss在计算上非常昂贵，特别是数据集很大的情况。

1.13 LogCosh Loss

1.13.1 介绍

• 计算 Loss 的双曲余弦对数。
• 这个函数比二次损失函数更平滑。
• 使用线性和二次平分方法，非常接近 Huber Loss。

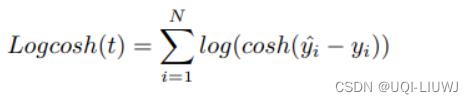
1.13.2 图像 

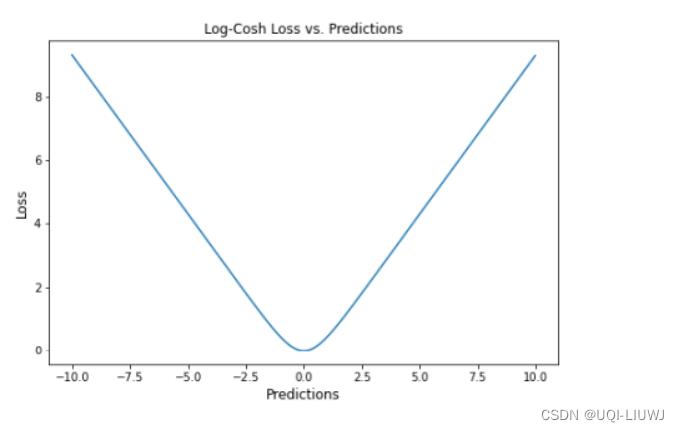1.13.3 优缺点

优点：

• 由于其连续性和可微性，它比Huber Loss 所需的计算要少

缺点

• 适应性不如Huber Loss，因为没有超参数进行调节