机器学习中的损失函数

Posted 2023-04-14

机器学习中的损失函数损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y,

参考技术A 机器学习中的损失函数
损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子：

其中，前面的均值函数表示的是经验风险函数，L代表的是损失函数，后面的是正则化项（regularizer）或者叫惩罚项（penalty term），它可以是L1，也可以是L2，或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的值。下面主要列出几种常见的损失函数。
一、log对数损失函数（逻辑回归）
有些人可能觉得逻辑回归的损失函数就是平方损失，其实并不是。平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到，而逻辑回归得到的并不是平方损失。在逻辑回归的推导中，它假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值等等。而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为：最小化负的似然函数（即max F(y, f(x)) —-> min -F(y, f(x)))。从损失函数的视角来看，它就成了log损失函数了。
log损失函数的标准形式：
L(Y,P(Y|X))=?logP(Y|X)L(Y,P(Y|X))=?log?P(Y|X)刚刚说到，取对数是为了方便计算极大似然估计，因为在MLE中，直接求导比较困难，所以通常都是先取对数再求导找极值点。损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下，使概率P(Y|X)达到最大值（换言之，就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说什么样的参数才能使我们观测到目前这组数据的概率最大）。因为log函数是单调递增的，所以logP(Y|X)也会达到最大值，因此在前面加上负号之后，最大化P(Y|X)就等价于最小化L了。
逻辑回归的P(Y=y|x)表达式如下：P(Y=y|x)=11+exp(?yf(x))P(Y=y|x)=11+exp(?yf(x))

将它带入到上式，通过推导可以得到logistic的损失函数表达式，如下：

L(y,P(Y=y|x))=log(1+exp(?yf(x)))L(y,P(Y=y|x))=log?(1+exp(?yf(x)))
逻辑回归最后得到的目标式子如下：

如果是二分类的话，则m值等于2，如果是多分类，m就是相应的类别总个数。这里需要解释一下：之所以有人认为逻辑回归是平方损失，是因为在使用梯度下降来求最优解的时候，它的迭代式子与平方损失求导后的式子非常相似，从而给人一种直观上的错觉。
这里有个PDF可以参考一下：Lecture 6: logistic regression.pdf.
二、平方损失函数（最小二乘法, Ordinary Least Squares ）
最小二乘法是线性回归的一种，OLS将问题转化成了一个凸优化问题。在线性回归中，它假设样本和噪声都服从高斯分布（为什么假设成高斯分布呢？其实这里隐藏了一个小知识点，就是中心极限定理，可以参考【central limit theorem】），最后通过极大似然估计（MLE）可以推导出最小二乘式子。最小二乘的基本原则是：最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。换言之，OLS是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢（即Mean squared error， MSE），主要有以下几个原因：
简单，计算方便；
欧氏距离是一种很好的相似性度量标准；
在不同的表示域变换后特征性质不变。
平方损失（Square loss）的标准形式如下：
(Y,f(X))=(Y?f(X))2L(Y,f(X))=(Y?f(X))2
当样本个数为n时，此时的损失函数变为：

Y-f(X)表示的是残差，整个式子表示的是残差的平方和，而我们的目的就是最小化这个目标函数值（注：该式子未加入正则项），也就是最小化残差的平方和（residual sum of squares，RSS）。
而在实际应用中，通常会使用均方差（MSE）作为一项衡量指标，公式如下：
MSE=1n∑i=1n(Yi~?Yi)2MSE=1n∑i=1n(Yi~?Yi)2
上面提到了线性回归，这里额外补充一句，我们通常说的线性有两种情况，一种是因变量y是自变量x的线性函数，一种是因变量y是参数的线性函数。在机器学习中，通常指的都是后一种情况。
三、指数损失函数（Adaboost）
学过Adaboost算法的人都知道，它是前向分步加法算法的特例，是一个加和模型，损失函数就是指数函数。在Adaboost中，经过m此迭代之后，可以得到:

Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数 和G：

而指数损失函数(exp-loss）的标准形式如下

可以看出，Adaboost的目标式子就是指数损失，在给定n个样本的情况下，Adaboost的损失函数为：

关于Adaboost的推导，可以参考Wikipedia：AdaBoost或者《统计学习方法》P145.
四、Hinge损失函数（SVM）
在机器学习算法中，hinge损失函数和SVM是息息相关的。在线性支持向量机中，最优化问题可以等价于下列式子：

下面来对式子做个变形，令：

于是，原式就变成了：

如若取，式子就可以表示成：

可以看出，该式子与下式非常相似：

前半部分中的就是hinge损失函数，而后面相当于L2正则项。
Hinge 损失函数的标准形式
可以看出，当|y|>=1时，L(y)=0。
更多内容，参考Hinge-loss。
补充一下：在libsvm中一共有4中核函数可以选择，对应的是-t参数分别是：
0-线性核；
1-多项式核；
2-RBF核；
3-sigmoid核。
五、其它损失函数
除了以上这几种损失函数，常用的还有：
0-1损失函数

绝对值损失函数

下面来看看几种损失函数的可视化图像，对着图看看横坐标，看看纵坐标，再看看每条线都表示什么损失函数，多看几次好好消化消化。

OK，暂时先写到这里，休息下。最后，需要记住的是：参数越多，模型越复杂，而越复杂的模型越容易过拟合。过拟合就是说模型在训练数据上的效果远远好于在测试集上的性能。此时可以考虑正则化，通过设置正则项前面的hyper parameter，来权衡损失函数和正则项，减小参数规模，达到模型简化的目的，从而使模型具有更好的泛化能力。

机器学习中的目标函数损失函数代价函数有什么区别？

作者：zzanswer
链接：https://www.zhihu.com/question/52398145/answer/209358209
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

谢谢评论区

@阿萨姆

老师的建议，完善下答案：

 

首先给出结论：损失函数和代价函数是同一个东西，目标函数是一个与他们相关但更广的概念，对于目标函数来说在有约束条件下的最小化就是损失函数（loss function）。

举个例子解释一下:（图片来自Andrew Ng Machine Learning公开课视频）

 

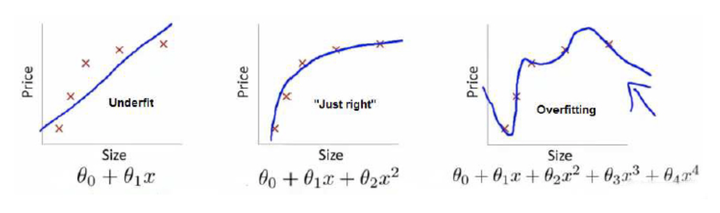
上面三个图的函数依次为 , , 。我们是想用这三个函数分别来拟合Price，Price的真实值记为 。

我们给定 ，这三个函数都会输出一个 ,这个输出的 与真实值 可能是相同的，也可能是不同的，为了表示我们拟合的好坏，我们就用一个函数来度量拟合的程度，比如：

，这个函数就称为损失函数(loss function)，或者叫代价函数(cost function)。损失函数越小，就代表模型拟合的越好。

那是不是我们的目标就只是让loss function越小越好呢？还不是。

这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望，这是由于我们输入输出的 遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集， 关于训练集的平均损失称作经验风险(empirical risk)，即 ，所以我们的目标就是最小化 ，称为经验风险最小化。

到这里完了吗？还没有。

如果到这一步就完了的话，那我们看上面的图，那肯定是最右面的 的经验风险函数最小了，因为它对历史的数据拟合的最好嘛。但是我们从图上来看 肯定不是最好的，因为它过度学习历史数据，导致它在真正预测时效果会很不好，这种情况称为过拟合(over-fitting)。

为什么会造成这种结果？大白话说就是它的函数太复杂了，都有四次方了，这就引出了下面的概念，我们不仅要让经验风险最小化，还要让结构风险最小化。这个时候就定义了一个函数 ，这个函数专门用来度量模型的复杂度，在机器学习中也叫正则化(regularization)。常用的有 , 范数。

到这一步我们就可以说我们最终的优化函数是： ，即最优化经验风险和结构风险，而这个函数就被称为目标函数。

结合上面的例子来分析：最左面的 结构风险最小（模型结构最简单），但是经验风险最大（对历史数据拟合的最差）；最右面的 经验风险最小（对历史数据拟合的最好），但是结构风险最大（模型结构最复杂）;而 达到了二者的良好平衡，最适合用来预测未知数据集。

以上的理解基于Coursera上Andrew Ng的公开课和李航的《统计学习方法》,如有理解错误，欢迎大家指正。