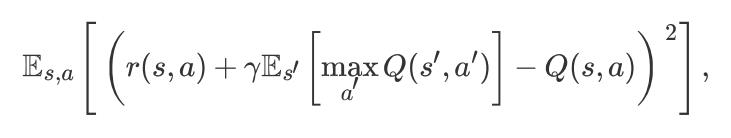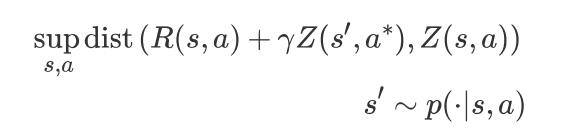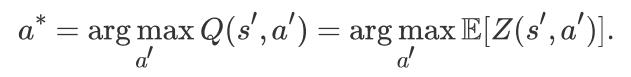基础的强化学习(RL)算法及代码详细demo

Posted 2023-03-29 Promethe_us

文章目录

• • • 一、Sarsa (悬崖问题)
    • • 1.1 CliffWalking-v0环境介绍
      • 1.2 Sarsa算法流程
      • 1.3 具体代码
      • 1.4 演示效果
    • 二、Q-Learning (悬崖问题)
    • • 2.1 CliffWalking-v0环境介绍
      • 2.2 Q-Learning算法流程
      • 2.3 具体代码
      • 2.4 演示效果
    • 三、PG 策略梯度 (倒立摆)
    • • 3.1 CartPole-v1环境介绍
      • 3.2 PG算法流程(REINFORCE)
      • 3.3 具体代码
      • 3.4 演示效果
    • 四、PPO (飞船降落)
    • • 4.1 LunarLander-v2环境介绍
      • 4.2 PPO-Clip算法流程
      • 4.3 具体代码
      • 4.4 演示效果
    • 五、DQN (打砖块)
    • • 5.1 Breakout-v0环境介绍
      • 5.2 DQN算法流程
      • 5.3 具体代码
      • 5.4 演示效果
    • 六、DDPG (单摆)
    • • 6.1 Pendulum-v1环境介绍
      • 6.2 DDPG算法流程
      • 6.3 具体代码
      • 6.4 演示效果

• gym环境: https://www.gymlibrary.dev/

• 环境安装:

  • 我的版本:

    package	module
    gym	0.24.0
    ale-py	0.7.5
    torch	1.11.0
    torchvision	0.12.0
    tensorboard	2.6.0

  • 安装方法：

    pip install -i https://pypi.tuna.tsinghua.edu.cn/simple gym
    pip install --no-index -f https://github.com/Kojoley/atari-py/releases atari_py
    pip install gym[atari]
    pip uninstall ale-py
    pip install ale-py
    

    安装box2d: 可能会遇到building wheel failed for box2d

    在 https://www.lfd.uci.edu/~gohlke/pythonlibs/ 下载相应的 PyBox2D的whl文件
    然后在命令行:
    pip install D:\\FILES\\PYTHON_PROJECTS\\Box2D-2.3.10-cp37-cp37m-win_amd64.whl
    

一、Sarsa (悬崖问题)

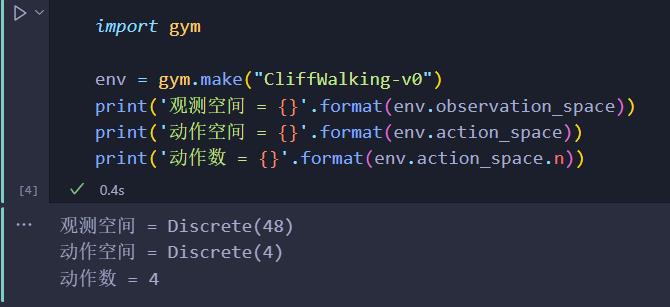
1.1 CliffWalking-v0环境介绍

在一个4x12的网格中，智能体以网格的左下角位置为起点，以网格的下角位置为终点，目标是移动智能体到达终点位置，智能体每次可以在上、下、左、右这4个方向中移动一步，每移动一步会得到 -1 的奖励。

• 如果智能体“掉入悬崖” ，会立即回到起点位置，并得到-100单位的奖励

• 当智能体移动到终点时，该回合结束，该回合总奖励为各步奖励之和

import gym

env = gym.make("CliffWalking-v0")
observation = env.reset() 
env.render()

• 从起点到终点最少需要13步，每步得到-1的reward。我们的目标也是要通过RL训练出一个模型，使得该模型能在测试中一个episode的reward能够接近于-13左右。

1.2 Sarsa算法流程

算法参数: 步长$\alpha <1$ 极小值$ϵ$ （两个超参数)

对于所有$Q(s,a)$随机初始化，终点处$ Q(s_end,a) = 0$

for (each trajectory):

初始化$S$

$a_t=ϵ-greedy(s_t)$

for (each step):

执行$a_t$，得到$(r_{t+1},s_{t+1})$

$a_{t+1}=ϵ-greedy(s_{t+1})$

$Q(s_t,a_t)=Q(s_t,a_t)+\alpha [r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)]$

$s_t=s_{t+1},a_t=a_{t+1}$

1.3 具体代码

import numpy as np
import gym
import time

class SarsaAgent:
    def __init__(self, obs_n, act_n, learning_rate=0.01, gamma=0.9, e_greed=0.1):
        self.act_n = act_n
        self.lr = learning_rate
        self.gamma = gamma
        self.epsilon = e_greed
        self.Q = np.zeros((obs_n, act_n))
    # e_greed:根据s_t,选择a_t
    def sample(self,obs):
        if np.random.uniform(0,1) < (1.0 - self.epsilon):
            action = self.predict(obs)
        else:
            action = np.random.choice(self.act_n) # 0,1,2,3
        return action
    # a_t = argmax Q(s)
    def predict(self, obs):
        Q_list = self.Q[obs, :] #当前s下所有a对应的Q值
        maxQ = np.max(Q_list)
        action_list = np.where(Q_list == maxQ)[0] # action_list=所有=Qmax的索引
        action = np.random.choice(action_list)
        return action
    
    def learn(self, obs, action, reward, next_obs, next_action, done): # (S,A,R,S,A)
        '''
        done: episode是否结束
        '''
        predict_Q = self.Q[obs,action]
        if done:
            target_Q = reward
        else:
            target_Q = reward + self.gamma * self.Q[next_obs,next_action]
        # 更新Q表格
        self.Q[obs,action] += self.lr * (target_Q - predict_Q)
    def save(self):
        npy_file = './q-table.npy'
        np.save(npy_file, self.Q)
        print(npy_file + ' saved.')
    def load(self, npy_file='./q_table.npy'):
        self.Q = np.load(npy_file)
        print(npy_file + ' loaded.')

def run_episode(env, agent, render=False):
    total_steps = 0 # 记录当前episode走了多少step
    total_reward = 0 
    obs = env.reset()
    action = agent.sample(obs)
    while True:
        next_obs, reward, done, _ = env.step(action)
        next_action = agent.sample(next_obs)
        agent.learn(obs, action, reward, next_obs, next_action, done)
        action = next_action
        obs = next_obs
        total_reward += reward
        total_steps += 1
        if render:
            env.render()
            time.sleep(0.)
        if done:
            break
    return total_reward, total_steps

def test_episode(env, agent): 
    total_steps = 0 # 记录当前episode走了多少step
    total_reward = 0 
    obs = env.reset()
    while True:
        action = agent.predict(obs)
        next_obs, reward, done, _ = env.step(action)
        total_reward += reward
        total_steps += 1
        obs = next_obs
        time.sleep(0.5)
        env.render()
        if done:
            break
    return total_reward, total_steps

def main():
    env = gym.make("CliffWalking-v0")
    agent = SarsaAgent(obs_n=env.observation_space.n, 
                       act_n=env.action_space.n,
                       learning_rate=0.025, gamma=0.9, e_greed=0.1)
    for episode in range(1000):
        total_reward, total_steps = run_episode(env, agent, False)
        print('Episode %s: total_steps = %s , total_reward = %.1f' % (episode, total_steps, total_reward))
    test_episode(env, agent)

main()

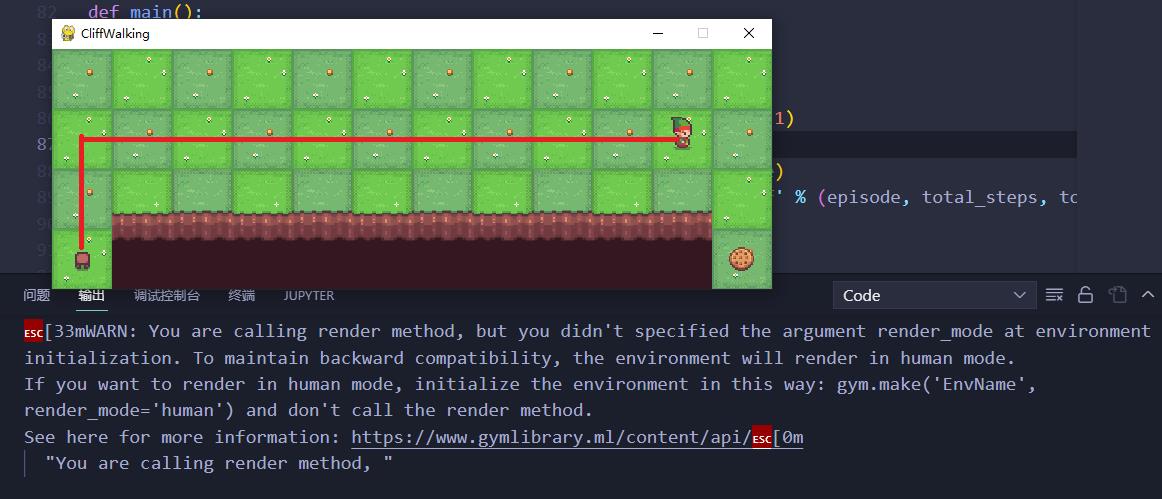
1.4 演示效果

训练了1000个episode,$reward=-23$

二、Q-Learning (悬崖问题)

2.1 CliffWalking-v0环境介绍

(介绍见1.1)

2.2 Q-Learning算法流程

(Q-Learning其实真正执行的策略和Sarsa是一样的，只不过学习的策略是保守的最优策略)

算法参数: 步长$\alpha <1$ 极小值$ϵ$ （两个超参数)

对于所有$Q(s,a)$随机初始化，终点处$Q(s_{end},a)=0$
for (each trajectory):

初始化$S$

for (each step):

$a_t=ϵ-greedy(s_t)$（行为策略）

执行$a_t$，得到$(r_{t+1},s_{t+1})$

Q ( s t , a t ) = Q ( s t , a t ) + α [ r t + 1 + γ m a x a Q ( s t + 1 , a ) − Q ( s t , a t ) ] Q(s_t,a_t)=Q(s_t,a_t)+\\alpha[r_t+1+\\gamma \\undersetam

分布式强化学习基础概念（Distributional RL ）

 

分布式强化学习基础概念（Distributional RL）

 

from: https://mtomassoli.github.io/2017/12/08/distributional_rl/

1. Q-learning

在 Q-learning 中，我们想要优化如下的 loss：

　　

Distributional RL 的主要思想是：to work directly with the full distribution of the return rather than with its expectation.

假设随机变量 Z(s, a) 是获得的回报（return），那么：Q(s, a) = E(Z(s, a)) ; 并非像公式（1）中所要最小化的误差那样，也就是 期望的距离。

我们可以直接最小化这两个分布之间的距离，which is a distance between full distribution：

其中，R(s, a) 是即刻奖赏的随机变量，sup 是函数值的上界的意思，英文解释为：supremum。并且：

注意的是，我们依然用的是 Q(s, a)，但是，此处我们尝试优化 distributions，而不是这些分布的期望。

 

2. Policy Evaluation：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Reference Paper：

1. https://arxiv.org/pdf/1707.06887.pdf 

2. https://arxiv.org/pdf/1710.10044.pdf

 

 

 

以上是关于基础的强化学习(RL)算法及代码详细demo的主要内容，如果未能解决你的问题，请参考以下文章

强化学习入门笔记 | UCL silver RL | UC Berkely cs285 DRL

人工智能基础：机器学习常见的算法介绍

强化学习常用算法+实际应用 ，必须get这些核心要点！

第三章 动态规划-基于模型的RL

离线强化学习的乐观观点

用强化学习通关超级马里奥！