第三章 动态规划-基于模型的RL

Posted 2021-04-18 深度强化学习在生产调度中的应用

动态规划(DP)这个术语指的是一组算法，它们可以在给定一个完美的环境模型作为马尔可夫决策过程(MDP)的情况下，用来计算最优策略。经典的DP算法假设模型是完美的，计算量大，在强化学习中应用有限，但在理论上仍然很重要。DP为理解后续将会介绍的方法提供了必要的基础。事实上，所有这些方法都可以被看作试图实现与DP几乎相同的效果，只是计算量更少，而且没有假设一个完美的环境模型。

DP和一般强化学习的核心思想是使用值函数来组织和构造对好策略的搜索。在本章中，我们将展示如何使用DP来计算值函数。正如前面所讨论的，一旦找到满足贝尔曼最优方程的最优值函数v_*或q_*，就可以很容易地获得最优策略：

 （1）

或

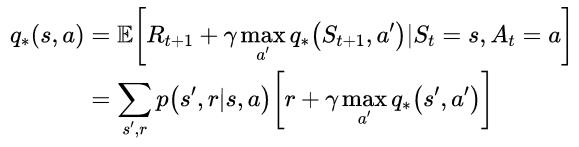（2）

对于所有的s∈S，a∈A(s)，s’∈S⁺。我们将看到，DP算法是通过将这些贝尔曼方程转化为赋值，也就是说，转化为改进期望值函数近似值的更新规则而得到的。

3.1 学习目标

• 理解策略评估和处理改进之间区别，以及这些过程如何交互的；

• 理解策略迭代算法；

• 理解值迭代算法；

• 理解动态规划方法的局限性。

3.2  策略评估（预测）

首先，我们考虑如何计算任意策略π的状态值函数v_π，这在DP文献中被称为策略评估，我们也把它称为预测问题。回想上一章中，对于虽有的s∈S，

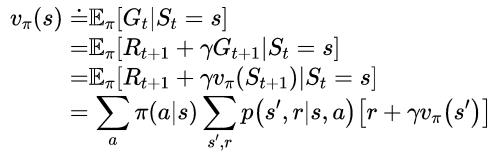（3-4）                             

其中π(a|s)是策略π在状态s下执行动作a的概率，带下标π的期望表示其以遵循的策略π为条件。只要满足γ<1或者在策略π下，所有状态都会有终止状态，那么v_π就是存在且唯一的。

如果环境的动态转移特性是完全可知的，那么上式其实就是|S|个线性方程，带有|S|个未知数。原则上，可以进行直接求解，尽管有些繁琐。对于我们来说，迭代的计算方式是最适合的。假设我们有一系列的近似值函数v₀,v₁,v₂...，每一个都把状态集合S⁺映射到实数集R。初始的近似值函数v₀是任意选择的，然后后面的每一个近似值函数都使用v_π的贝尔曼方程（式（4））作为更新规则迭代求解。                                    

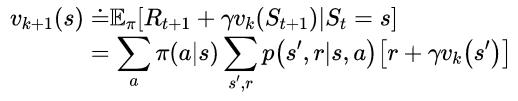（5）

显然v_k=v_π是这个更新规则的不动点，因为v_π的Bellman方程保证了我们在这种情况下是相等的。因此随着k→∞，序列{v_k}在保证v_π存在的条件下一般收敛到v_π。这种算法称为迭代策略评估。

为了从v_k得到后续的每一个近似v_k+1，迭代策略评估针对每个状态s进行相同的操作：把当前状态s的旧值更新成一个新值，这个新值是由状态s后一状态的旧值和期望即时奖励，在待评估策略下沿着所有可能的状态转移概率求和得到。我们把这个迭代操作叫做期望更新（expectedupdate）。迭代策略更新中的每次迭代都会更新一次所有的状态（fullback up，完全备份），以得到v_k+1的近似值函数。期望更新有多种不同的方式，这取决于当前更新的是状态（此处）还是状态-动作对，以及后一状态的估计值合并的方式。在DP算法中完成的所有更新都叫做期望更新，是因为这些更新都基于所有可能的下一状态的期望，而不是采用后一状态。

如果你想写一个描述迭代策略评估的程序，那么你应该使用两个数组，其中一个保存旧值v_k(s)，另一个保存新值v_k+1(s)。这样的话，新值就可以在不改变旧值的情况下被一个个计算出来。当然只使用一个数组更容易，可以用“in place”的方式更新值。这种方式下，某个状态更新后的值就会立即覆盖掉旧值。然后，根据状态更新的顺序，有时在式(5)的右边使用新值而不是旧值（可以这么理解：有时候恰好某个状态A的值更新较频繁，因为它与其他状态联系比较多，这样有可能下一次其他状态用到的A的值就是其更新两次或多次之后的）。“in place”算法同样也会收敛到v_π，实际上通常其收敛速度快于使用两个数组的版本，因为一旦可用就使用某状态的新值。我们认为更新是在状态空间的扫描中完成的。对于“in place”算法，状态值在扫描期间更新的顺序对收敛速度有显著影响。当我们考虑DP算法的时候，通常都考虑“in place”形式。

虽然策略迭代评估最终肯定会收敛，但是实际程序中我们需要设置一个终止条件。一个典型的终止条件就是当max_s∈S|v_k+1(s)-v_k(s)|的值非常小的时候，就让程序停止。

图1 迭代策略评估

3.3 策略改进

计算策略值函数的目的就是寻找更优的策略。假设已经确定了任一确定性策略π的值函数v_π，那么对于某一状态s，我们想要知道是不是可以改变一下策略来确定性地选择一个动作a≠v(s)。我们已经知道在状态s遵循当前策略的好坏，即v_π(s)，但是变成新策略后是变好了呢还是变坏了呢？一种方法就是在s考虑选择a，之后遵循现有的策略π，此时value迭代如下：                  

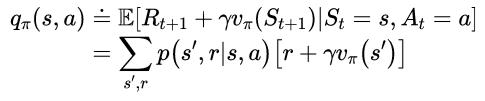（6）

关键标准是其是否大于v_π(s)，如果大于，说明在s选择a，之后遵循策略π会优于一直遵循策略π，那么在每次遇到状态s时仍然选择a会更好，新的策略在整体也更优。

这是一个称为策略改进定理（policy improvement theorem）的一般结果的特殊情况。设π和π’任意确定策略对，对于所有s∈S，有

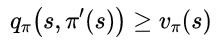           （7）

那么策略π’等同于或优于策略π，也就是说对于所有s∈S，其必会获得更大或相等的期望回报：

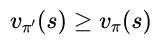                     （8）

而且，在任意状态下，如果式（7）存在严格不等式，那么在对应状态式（8）也必然是严格不等式。

策略改进理论适应于两个策略，原始的确定性策略π和改变的策略π’，π’与π的区别仅仅在于π’(s)=a≠π(s)。对于除了s的状态，式（7）成立因为两边相等，因此如果q_π(s,a)> v_π(s)，那么改变的策略优于π。

从式（7）出发，不断使用式（6）分解q_π，然后重新应用式（7）直到得到v_π’(s)：                        

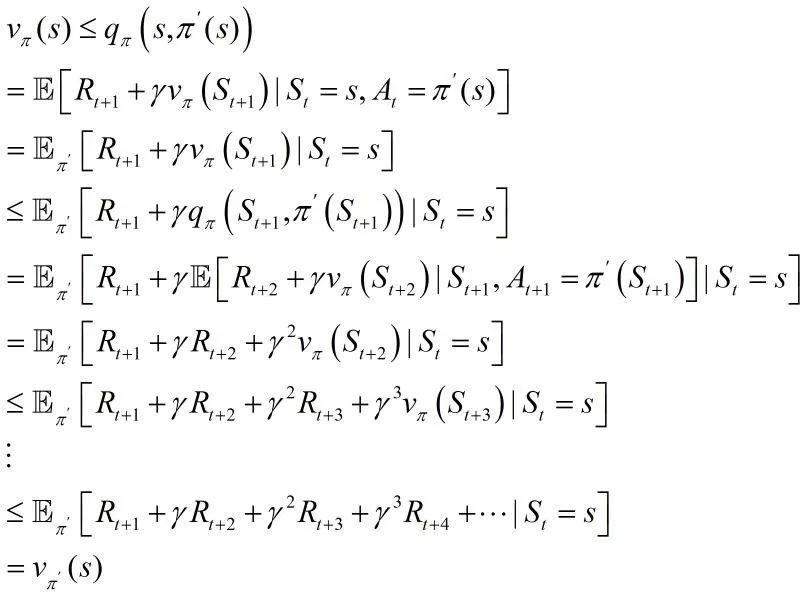（9）

到目前为止，我们已经了解了如何在给定策略及其值函数的情况下，轻松地评估策略在单个状态下对特定动作的更改，很自然地可以考虑在所有状态下改变所有可能的动作，根据q_π(s,a)在每个状态选择看起来最好的动作。换句话说，考虑如下的贪婪策略：                                

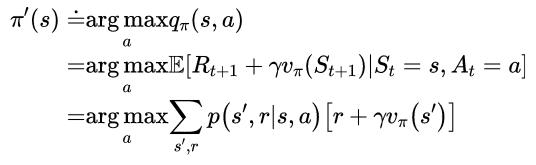（10）

贪婪策略根据v_π采取短期看起来（一步向前看）最优的动作，其满足式（7）策略改进理论的条件，所以可知其等同于或优于原始策略。通过使新策略对原策略的值函数贪婪，从而对原策略进行改进，这样制定新策略的过程称为策略改进（policyimprovement）。

假设新的贪婪策略π’和原策略π一样好，那么v_π’=v_π，根据式（10）对于所有s∈S，其满足：                                                             

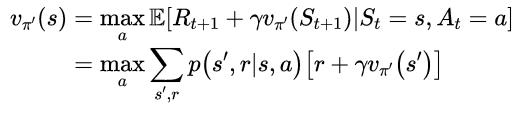（11）

这和贝尔曼最优方程是一样的，因此v_π’一定是v_*，π和π’都是最优策略。换句话说，策略改进一定会给我们一个更好地策略，除非我们当前的策略已经是最优的了。

3.4 策略迭代

一旦一个策略π使用v_π得到了改进并得到了更优的策略π’，然后就可以计算v_π’，并再次对其进行改进从而得到更优的π''，由此我们可以得到一个单调改进策略和值函数的序列：                                   

（12）

其中带有E的箭头表示策略评估，带有I的箭头表示策略改进，每个策略都保证比前一个策略有严格的改进(除非它已经是最优的)。由于有限的MDP只有有限数量的策略，因此该过程必然在有限次迭代中收敛到最优策略和最优值函数。

这种寻找最优策略的方法称为策略迭代，下面给出了其完整的算法。注意，每个策略评估本身就是一个迭代计算，从前一个策略的值函数开始。这通常会大大提高策略评估的收敛速度(可能是因为值函数在策略之间变化不大)。

图2 策略迭代