ACM入门之平衡树

Posted 2022-04-27 辉小歌

有时间补完。

---

---

---

平衡树：就是一个平衡的二叉搜索树。
平衡树的各个操作的时间为：logn

按照对二叉搜索树进行的"操作"可以分为一下几类：

• 有旋转：AVL、Splay、红黑树。
• 无旋转: 替罪羊、Treap。

例题:

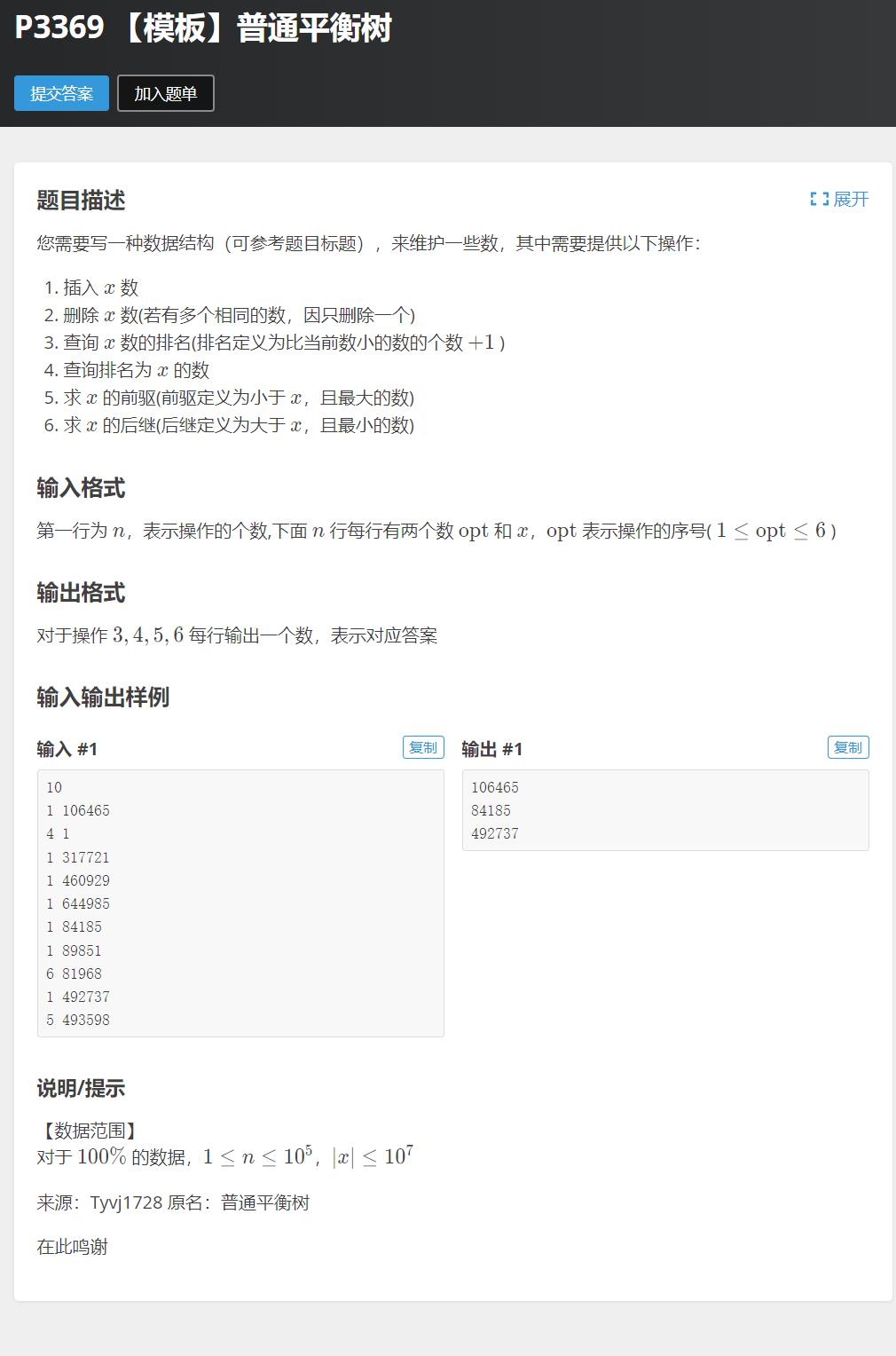
//抄的cnt大佬的代码
#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
using namespace std;
const int N = 100010, INF = 1e8;
int n;
struct Node

    int l, r;
    int k;
    int val;//堆中的编号
    int cnt, size;
tr[N];
int root, idx;
void pushup(int u)

    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + tr[u].cnt;//上传节点信息，更新size

int new_node(int k)

    tr[ ++ idx].k = k;
    tr[idx].val = rand();//尽量随机，随手给个就行
    tr[idx].cnt = 1;
    tr[idx].size = 1;
    return idx;

void zig(int &u)//左右旋，没啥好说的，自己在纸上画一下就知道了

    int q = tr[u].l;
    tr[u].l = tr[q].r;
    tr[q].r = u;
    u = q;
    pushup(tr[u].r);
    pushup(u);//最后一定要记得上传，不然完了

void zag(int &u)

    int q = tr[u].r;
    tr[u].r = tr[q].l;
    tr[q].l = u;
    u = q;
    pushup(tr[u].l);
    pushup(u);

void build()//建树操作，为了正确性增加两个哨兵，防止越界

    new_node(-INF), new_node(INF);
    root = 1, tr[1].r = 2;//初始化一下
    pushup(root);//上传信息
    if(tr[1].val< tr[2].val) zag(root);//不平衡了就旋转

void insert(int &u, int k)

    if(u == 0) u = new_node(k);//如果走到空了，就新建
    else
    
        if(tr[u].k == k)//如果找到了相同的节点，就cnt++
        
            tr[u].cnt ++;
        
        else
        
            if(tr[u].k > k)//否则看看是在左边还是在右边
            
                insert(tr[u].l, k);
                if(tr[tr[u].l].val > tr[u].val) zig(u);//不平衡立马调整
            
            else
            
                insert(tr[u].r, k);
                if(tr[tr[u].r].val > tr[u].val) zag(u); 
            
        
    
    pushup(u);//最后上传一下，是不是和线段树有点像啊？

void del(int &u, int k)//删除操作

    if(u == 0) return ;//如果没了说明节点不存在，就不管了。
    if(tr[u].k == k)//如果找到了这个点
    
        if(tr[u].cnt > 1) tr[u].cnt --;//大于一好说，直接cnt --
        else//不大于一
        
            if(tr[u].l || tr[u].r)//先看看是不是叶节点
            
                if(!tr[u].r || tr[tr[u].l].val) 
                
                    zig(u);
                    del(tr[u].r, k);//记得维护平衡哦
                
                else
                
                    zag(u);
                    del(tr[u].l, k);
                
            
            else u = 0;//是的话不用考虑平衡问题，直接删就是了
        
    
    else if(tr[u].k > k) del(tr[u].l, k);//如果没有找到就判断一下在左右两边的哪一边
    else del(tr[u].r, k);//找一下
    pushup(u);//上传更改

int get_rank(int u, int k)

    if(u == 0) return 0;//是0随便返回就行
    if(tr[u].k == k) return tr[tr[u].l].size + 1;//相等了那排名应该就是左边的数量加上自己
    if(tr[u].k > k) return get_rank(tr[u].l, k);//大了找左边
    return tr[tr[u].l].size + tr[u].cnt + get_rank(tr[u].r, k);//找右边
 
int get_key(int u, int rank)

    if(u == 0) return INF;
    if(tr[tr[u].l].size >= rank) return get_key(tr[u].l, rank);//找左边
    if(tr[tr[u].l].size + tr[u].cnt >= rank) return tr[u].k;//如果满足条件就直接return
    return get_key(tr[u].r, rank - tr[tr[u].l].size - tr[u].cnt);//不然就找右边

int get_pr(int u, int k)//前驱

    if(u == 0) return -INF;
    if(tr[u].k >= k) return get_pr(tr[u].l, k);//找左边
    return max(get_pr(tr[u].r, k), tr[u].k);//可能是右边可能是这个数，所以用个max

int get_ne(int u, int k)//后继

    if(u == 0) return INF;//后继的写法和前驱相反，大家可以注意一下
    if(tr[u].k <= k) return get_ne(tr[u].r, k);
    return min(get_ne(tr[u].l, k), tr[u].k);

int main()

    build();//建树，要是忘了就凉了
    cin >> n;
    while(n --)
    
        int op, x;
        cin >> op >> x;
        if(op == 1) insert(root, x);
        else if(op == 2) del(root, x);
        else if(op == 3) cout << get_rank(root, x) - 1 << endl;
        else if(op == 4) cout << get_key(root, x + 1) << endl;
        else if(op == 5) cout << get_pr(root, x) << endl;
        else cout << get_ne(root, x) << endl;//读入操作并进行处理
    
    return 0;