备战数学建模6-数据插值曲线拟合
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了备战数学建模6-数据插值曲线拟合相关的知识,希望对你有一定的参考价值。
目录
一、数据插值
1-数据插值的初步认识
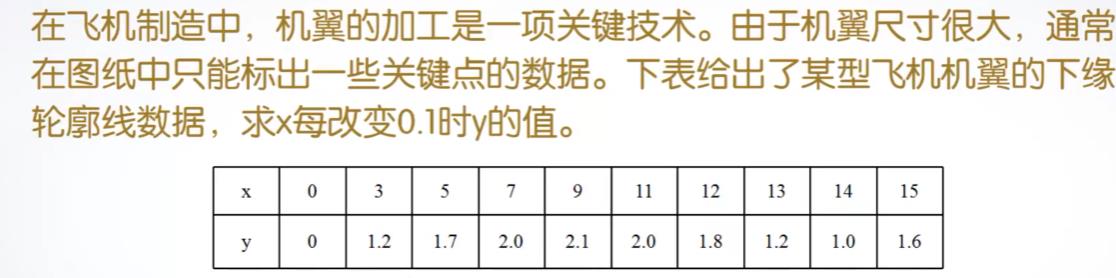
对于工程试验中,我们获取的往往是离散的数据,很难获取完备的连续的数据。数据插值可以根据有限个点的取值情况,合理估算出附近其它点的取值,从而节约大量的试验和测试资源,可以节约大量的人力和物力。
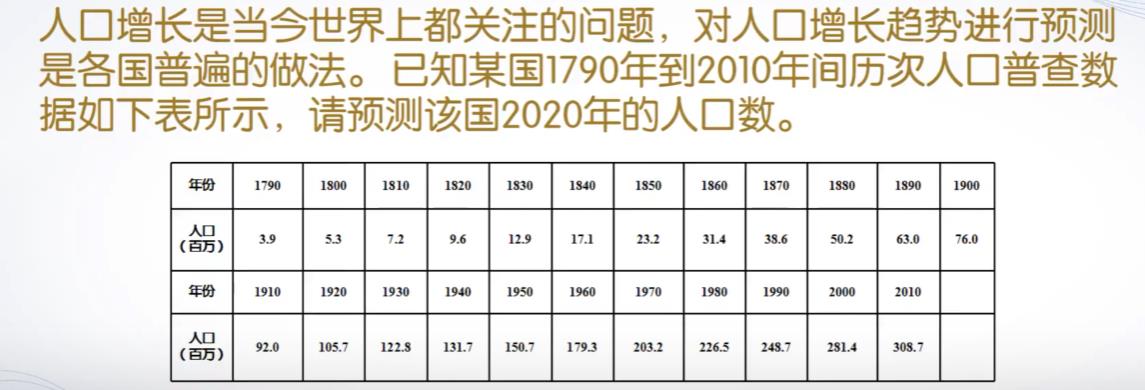
我们看一下上面零件加工的例子,从图中我们发现x和y是离散的点,我们需要利用插值,计算出x每改变0.1时y的值。代码如下,我们根据已知点,完成插值,并绘图观察。
x = [0,3,5,7,9,11,12,13,14,15] ;
y = [0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6] ;
x1 = 0 : 0.1 : 15 ; %需要的插值
y1 = interp1(x,y,x1,'spline') ;
plot(x1, y1) ;所绘制的图如下所示:
2-数据插值的计算机制
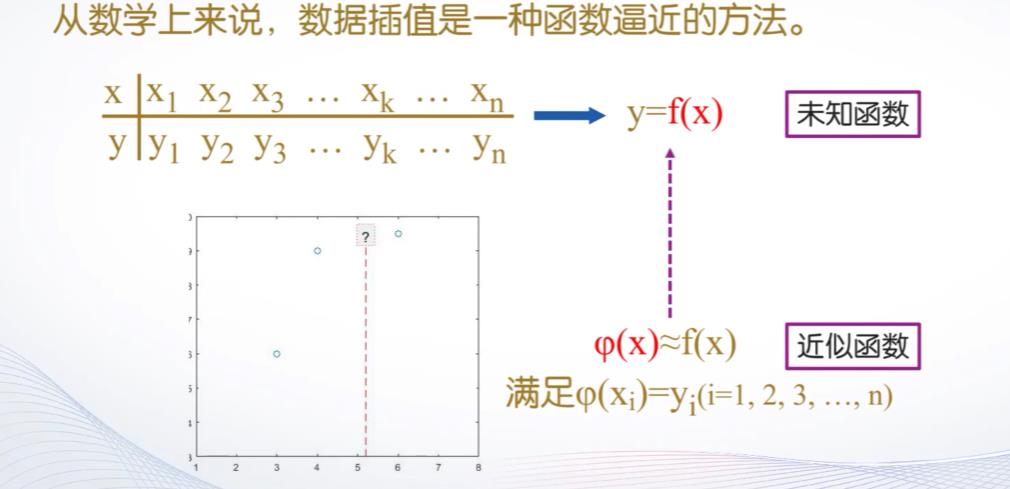
我们可以理解数据插值就算一种函数逼近的方法,就算就是根据离散数据点,找到一个近似函数去逼近未知函数,有了这个近似函数,我们就可以计算样本区间内的所有值了。
3-数据插值的实现方法
在MATLAB中我们使用interp1()函数进行一维插值。
调用格式如下所示:Y1 = interp1(X,Y,X1,method) ;其中X,Y为同维向量,根据X,Y的值,计算函数在X1处的值,X1是一个向量或者一个标量,表示要插入的点。method用于标记插值方法。
我们进一步看一下插入方法有如下四种:
(1)linear,线性插值,默认插值方法,将与插值点靠近的两个点用直线连接,然后在直线上选取插值点。
(2)nearest:最近点插值,选择最近样本点的值作为插值数据。
(3)pchip:分段3次埃米特插值。
(4)spline:三次样条插值。
注意:一般插值都使用3次多项式插值,而不是使用更高次多项式插值。因为次数过高,未必好,可能会产生震荡,从而偏离原函数。
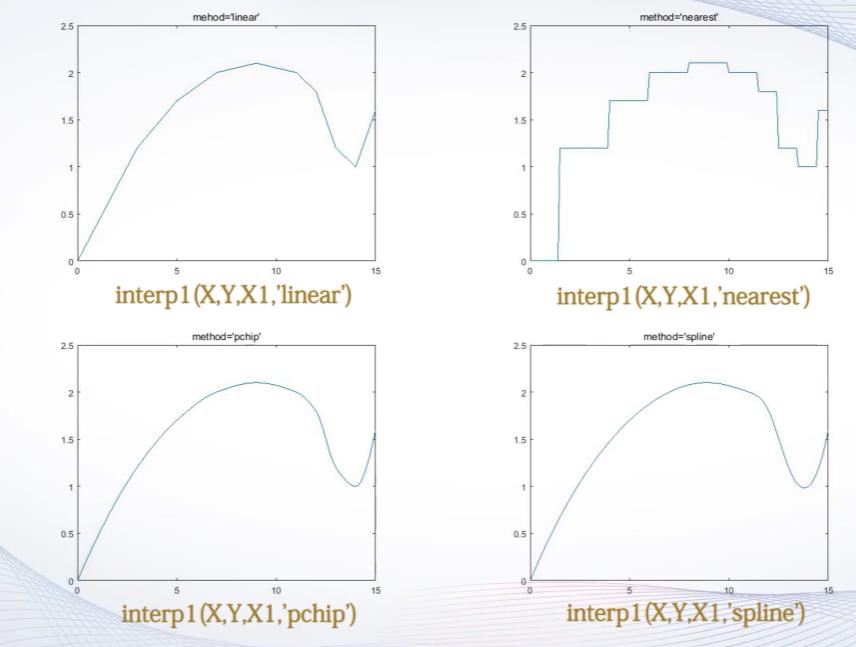
我们可以看一下,四种插值方式,插值后的曲线图,如下所示:
四种插值方法的比较:
线性插值和最近点插值比较简单,其中线性插值方法的计算量与样本点n无关,n越大,误差越小。
3次埃米特插值和3次样条插值效果都比较好,插值都能保证曲线的光滑性。
在MATLAB中我们使用interp2()函是实现二维插值。
函数的调用个数如下,Z = interp2(X,Y,Z,X1,Y1,method) ; 就是根据X,Y,Z对应的值,对于要插入的X1,Y1,求出采样点对应的函数值赋值给Z。method是插值方法。
4-数据插值的应用举例
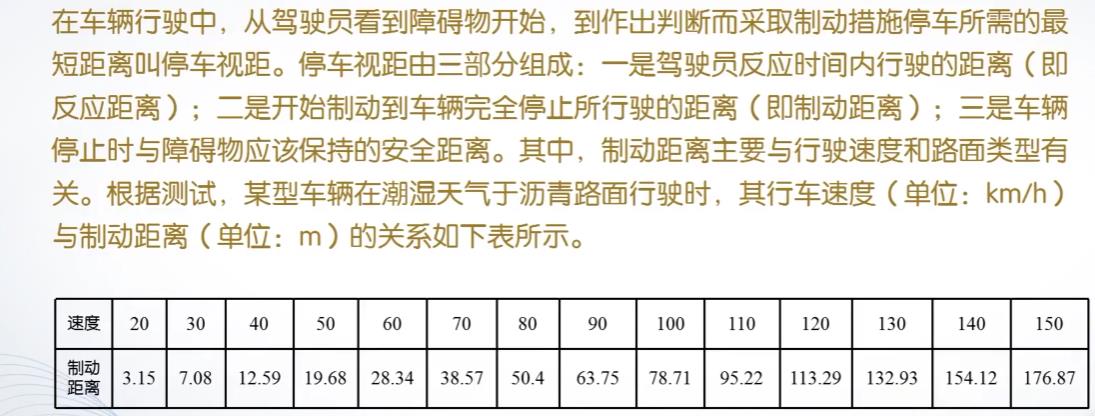
我们看一下下面的刹车制动问题,一个很好的数据插值案例。
通过分析,我们可以做一下假设,先假设车速为v,停车视距为d,反应距离为d1,制动距离为d2,安全距离为d3,反应时间为as,故可以得到:d1=as*v,d2是v的函数,具体的函数未知。
这样我们可以很容易列出一个方程:10*v+d2+10=120,但是我们只知道d2是v的函数,却解不出方程,其实这个题我们可以使用数据插值。
我们以表格总的数据作为样本,进行数据插值,计算处120m停车视距所对应的速度指标。
我们的编程思路如下:
第一步:建立速度与停车视距向量。
第二步:以1为单位,对采样区间内的所有速度进行插值,计算处相应的停车视距。
第三步:求出停车视距为120时对应的速度。
第四步:绘图。
对于第一问,时速最高不能超过36km/h。
v = 20 : 10 : 150 ; %速度向量
vs = v * 1000 / 3600 ; %将km/h转换为m/s
d1 = 10 * vs ; %反应距离
d2 = [3.15, 7.08, 12.59, 19.68, 28.34, 38.57, 50.4, 63.75, 78.71, 95.22, 113.29, 132.93, 154.12, 176.87] ;%制动距离
d3 = 10 ; %安全距离
d = d1 + d2 + d3 ; %停车视距
vi = 20 : 150 ; %要插入的速度样本点
di = interp1(v, d, vi, 'spline');
x = abs(di - 120) ; %得到一个新的向量
[y,i] = sort(x); %升序排序,最小元素的序号,就120的停车视距对应的速度序号
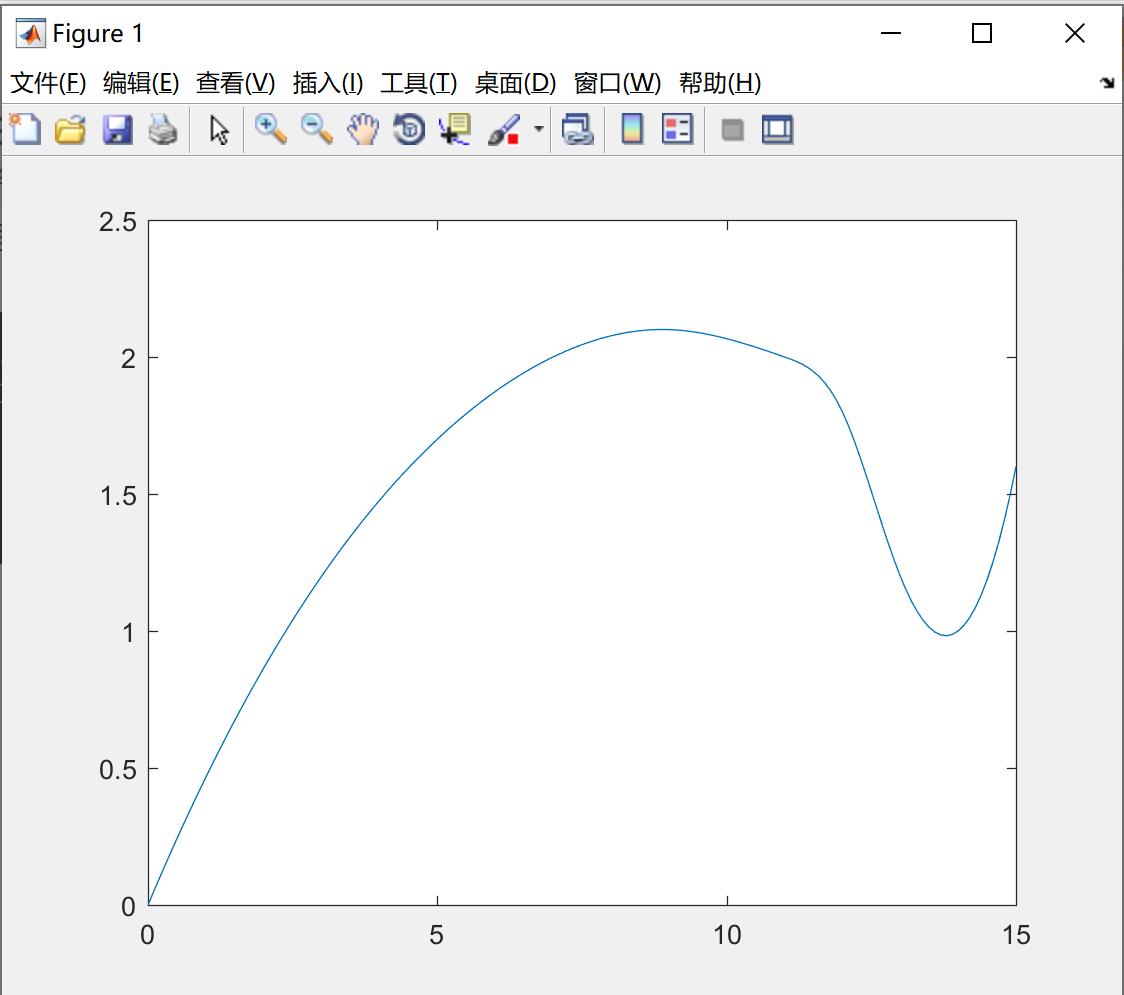
vi(i(1))
plot(vi, di, vi(i(1)), di(i(1)), 'rp') ; %绘图并标记速度与120m停车视距对应的坐标绘图观察如下所示:通过此图我们可以发现行车速度与停车视距的关系为非线性,非线性增长趋势。行车速度越快,要保证的停车视距越长。
对于第二问,在插值之后的代码中,加上如下代码,计算出125km/h的速度下,停车视距为ds=480.14m.
j = find(vi==125) ; %找到vi等于125时候,对应的下标
ds = di(j)通过上面的刹车问题,我们可以得出:公路设计是一个复杂的工程,除了地质,地形之外,
驾驶者的可视距离也要考虑在内。
二、曲线拟合
1-初识曲线拟合
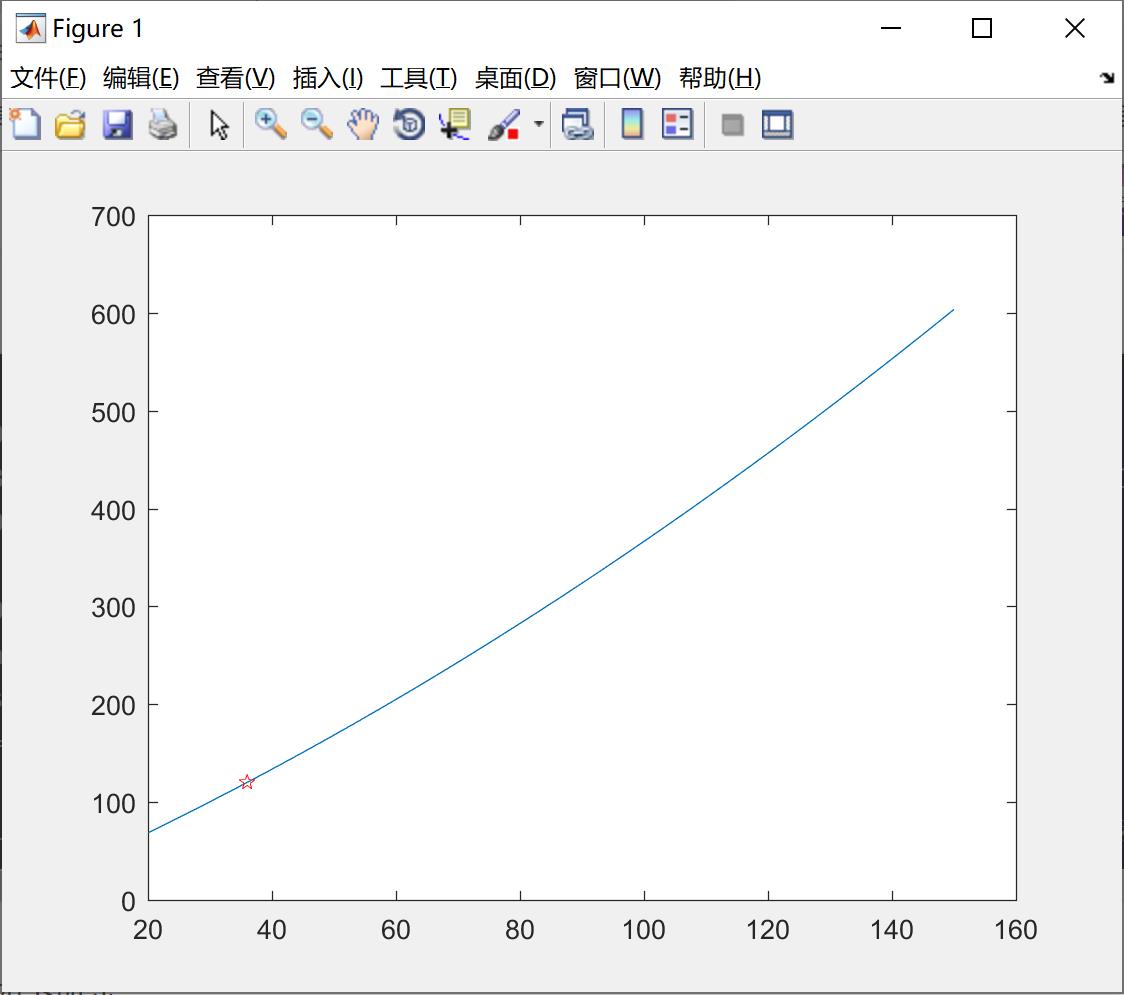
我们看下面的人口预测的例子,了解一下曲线拟合。
解题思路:我们通过找到一个函数,去逼近这些数据,然后再根据根据找到的函数,去求出预测点的值。代码如下:预测2020年的人口数量为 339.7869百万。
x = 1790 : 10 : 2010 ; %年份的向量
y = [3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.2, 31.4, 38.6, 50.2, 63, 76, 92, 105.7, 122.8, 131.7, 150.7, 179.3, 203.2, 226.5, 248.7,281.4,308.7 ] ;
plot(x,y,'*') ;%绘制散点图
p = polyfit(x,y,3) ; %生成三次多项式函数,系数保存在向量p中
polyval(p,2020) %计算多项式函数在2020处的函数值
hold on ;
plot(x, polyval(p,x)) ;%绘制拟合曲线绘制的散点图和拟合曲线如下所示:
2-曲线拟合的原理
其实我们会发现拟合的曲线并不是经过所有的散点,那么拟合曲线是怎么画出来的呢。
其实这个逼近有2个问题:
第一,用什么类型的函数作为逼近函数呢?多项式函数
第二,误差最小到底怎么计算?最小二乘法
最小二乘法:又称最小平方法,是一种数学优化技术,通过最小化误差的平方和来寻找数据的最佳函数匹配。
3-曲线拟合的实现方法
使用polyfit()函数实现多项式拟合,该函数的功能是求得最小二乘拟合多项式系数。
该函数有如下三种调用格式:
P = polyfit(X,Y,m)
[P,S] = polyfit(X,Y,m)
[P,S,mu] polyfit(X,Y,m)
根据样本X,Y产生一个m次的多项式P及其在采样点误差数据S,mu是一个二元向量,其中mu(1)是mean(X),mu(2)是std(X).
数据插值和曲线拟合的对比分析:
相同点:
1-都属于函数逼近方法。
2-都能进行数据估算。
不同点:
1-实现方法不同,数据插值要求逼近函数通过样本点,曲线拟合不要求逼近函数通过样本点,只要求总体误差最小。
2-结果形式不同,数据插值往往没有确定的函数表达式,曲线拟合则有。
3-数据插值一般用于样本区间内的区间估算,曲线拟合不仅可以预测区间内,也可以预测发展趋势。
4-样本数据是精确数据,可用数据插值方法,若样本数据是统计数据或存在误差,则适合用曲线拟合方法。
以上是关于备战数学建模6-数据插值曲线拟合的主要内容,如果未能解决你的问题,请参考以下文章