matlab怎么对曲线进行平滑啊？

Posted 2023-05-04

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了matlab怎么对曲线进行平滑啊？相关的知识，希望对你有一定的参考价值。

MATLAB中绘制平滑曲线一般使用最小二乘法或者B样条插值。
最小二乘法实际上是函数拟合，可以得到目标函数（这里为多项式）的系数，对outliers相对不敏感，缺点是需要预先设置目标函数的阶数，且有时不容易找到最优的目标函数形式。这里使用polyfit()函数进行多项式拟合，其他类似函数，如：lsqlin()不在讨论之列，用法有不同。
B样条插值是一种插值方法，得不到目标函数，但可以最大限度地在光滑的前提下接近采样点，对outliers敏感，只是比一般的多项式插值好点。
对照：plot()函数只是将采样点用直线连接在一起，结果是一条折线。

下面通过一个与条形图结合的实例对最小二乘法(least square)与B样条插值(B spline)进行分析：

1. y1=[15.81292 16.43826 5.696203; 10.91314 8.493151 5.379747; 10.24499 7.945205 8.860759; 12.02673 13.15068 19.62025;...
2. 5.790646 15.89041 37.34177; 7.349666 9.041096 6.012658; 10.69042 10.13699 3.797468; 16.03563 10.68493 5.696203;...
3. 11.13586 8.219178 7.594937];
4. y11=[15.81292,10.91314,10.24499,12.02673,5.790646,7.349666,10.69042,16.03563,11.13586];
5. y12=[16.43826,8.493151,7.945205,13.15068,15.89041,9.041096,10.13699,10.68493,8.219178];
6. y13=[5.696203,5.379747,8.860759,19.62025,37.34177,6.012658,3.797468,5.696203,7.594937];
7. x=[1 2 3 4 5 6 7 8 9];
8.
9. %% bar graph
10.b=bar([y11',y12',y13']);% same with b=bar(y1)
11.grid on;
12.set(gca, 'xticklabel', '0-20','20-40','40-60','60-80','80-100','100-120','120-140','140-160','160-180');
13.legend('156C','164C','172C');
14.xlabel('Angle:degree');
15.ylabel('Percentage:%');
16.title('Angle');
17.hold on;
18.
19.%% least square method
20.result1=polyfit(x,y11,3);
21.plot(x,polyval(result1,[1:9]));
22.
23.%% B spline
24.values1 = spcrv([[x(1) x x(end)];[y11(1) y11 y11(end)]],3);
25.plot(values1(1,:),values1(2,:),'b','LineWidth',2);
上例中，y1=y11', y12', y13' 对于bar()函数，使用二者都可以，但是对于least square与B spline，只能将y值分开；另外，bar()函数对于x轴的值有默认值，所以对于bar()，不写x=[...]仍可以执行，但对于least square与B spline，需明确指出x值。参考技术A matlab将曲线进行平滑的方法如下：

clc,clear；
a = 1:1:6；%横坐标
b = [8.0 9.0 10.0 15.0 35.0 40.0]； %纵坐标
plot(a, b, 'b')； %自然状态的画图效果
hold on；

第一种，画平滑曲线的方法：

c = polyfit(a, b, 2)； %进行拟合，c为2次拟合后的系数；
d = polyval(c, a, )1； %拟合后，每一个横坐标对应的值即为d；
plot(a, d, 'r')； %拟合后的曲线；

plot(a, b, '*')； %将每个点用*画出来；
hold on；

第二种，画平滑曲线的方法
values = spcrv([[a(1) a a(end)];[b(1) b b(end)]],3)；
plot(values(1,:),values(2,:), 'g')；参考技术B x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];
y=[8 70 118 100 9 0 5];
以上是每一个X和Y对应的坐标，请问如何编程能够绘制平滑曲线，这个图形就像二次函数一样的
如果要在图中绘制一条直线加上y=70的直线，用不同颜色区分！
x=[0 0.1 0.16 0.27 0.41 0.48 0.59 0.8];
y=[5 9 70 118 100 17 0 5];
y1=[22.8 22.8 22.8 22.8 22.8 22.8 22.8 22.8];
values1=spcrv([[x(1) x x(end)];[y(1) y y(end)]],3,1000);
values2=spcrv([[x(1) x x(end)];[y1(1) y1 y1(end)]],3,1000);
plot(values1(1,:),values1(2,:),'r',values2(1,:),values2(2,:),'b') 参考技术C >> x=[0 0.1 0.16 0.27 0.41 0.48 0.59 0.8];
y=[5 9 70 118 100 17 0 5];
y1=[22.8 22.8 22.8 22.8 22.8 22.8 22.8 22.8];
values1=spcrv([[x(1) x x(end)];[y(1) y y(end)]],3,1000);
values2=spcrv([[x(1) x x(end)];[y1(1) y1 y1(end)]],3,1000);
plot(values1(1,:),values1(2,:),'r',values2(1,:),values2(2,:),'b')
>>追问

谢谢啊！我这有很长的一组数据，一个一个输进去不太现实啊，该怎么办？不好意思啊，我是初学这个软件！

追答

很长一个数组？这个就。貌似都是可以输入的，这有一篇文章，你可以参考下~~~
http://philotack.blog.163.com/blog/static/37473423201010910230221/

希望可以帮助到你

追问

太感谢了！！！！！！！！！

本回答被提问者采纳

从零开始一起学习SLAM | 点云平滑法线估计

点击公众号“计算机视觉life”关注，置顶星标更快接收消息！
本文编程练习框架及数据获取方法见文末获取方式
菜单栏点击“知识星球”查看「从零开始学习SLAM」一起学习交流

点云滤波后为什么还需要平滑？

小白：师兄，师兄，上次你说的点云滤波我学会啦，下一步怎么把点云变成网格啊？
师兄：滤波只是第一步，在网格化前我们还需要对滤波后的点云进行平滑（smoothing）
小白：不是已经滤波了吗？怎么还要平滑啊？滤波和平滑不一样吗？
师兄：确实不太一样。我们用RGB-D，激光扫描仪等设备扫描物体，尤其是比较小的物体时，往往会有测量误差。这些误差所造成的不规则数据如果直接拿来曲面重建的话，会使得重建的曲面不光滑或者有漏洞，而且这种不规则数据很难用前面我们提到过的统计分析等滤波方法消除，所以为了建立光滑完整的模型必须对物体表面进行平滑处理和漏洞修复。
你看下面左边就是原始的扫描数据，右边就是用最小二乘法进行表面平滑后的结果

小白：从图上看，平滑确实效果很明显啊，左边杯子上黑色的是噪声吧，右边的结果来看经过平滑都消失了
师兄：对，除了上面说到的设备测量误差外，还有一种情况也需要对点云进行平滑。就是后处理过程中，比如我们对同一个物体从不同方向进行了多次扫描，然后把扫描结果进行配准，最后得到一个完整的模型，但是你配准的结果不一定准啊，比如下图中左侧就是配准后未经过处理的结果，同一面墙壁由于配准误差变成了“两面墙”，并不能完全重叠，你觉得这个数据可以直接用来进行表面重建吗？

小白：好坑啊，肯定不行，这样重建出的结果也是两面墙了吧
师兄：对，所以我们需要想办法把“两面墙”变成“一面墙”，如果这时候，我们没有条件重新扫描出更精确的结果，或者配准精度也无法提升，可以通过重采样的方法来实现点云的平滑，从而避免出现这样的问题。
小白：原来这个平滑这么重要啊！怎么用重采样来平滑呢？感觉迫不及待想要学习啦！
师兄：（既然胃口已经被吊起来了）那我们赶快开始切入正题吧

如何通过重采样实现点云平滑？

师兄：点云重采样，我们实际上是通过一种叫做“移动最小二乘”（MLS， Moving Least Squares ）法来实现的，对应的类名叫做：pcl::MovingLeastSquares，你知道怎么用吗？
小白：不知道，不过我还记得我们上次师兄给我说的方法，在PCL API documentation http://docs.pointclouds.org/trunk/ 上查询类名称，就能看到类的定义和用法啦
师兄：活学活用啊，哈哈，那我们现在去查一下看看吧
小白：嗯，我查到了，这个MLS类的定义在这里：
http://docs.pointclouds.org/trunk/classpcl_1_1_moving_least_squares.html#a379330b0b1dacaa668d165f94930749c
成员函数好多啊
师兄：对，看着是很多，但是很多我们不常用的，比如我们常用的一个用于重采样的示例代码如下，每行代码都给你注释好了，结合上面网址看很容易理解

// 对点云重采样  
pcl::search::KdTree<PointT>::Ptr treeSampling (new pcl::search::KdTree<PointT>); // 创建用于最近邻搜索的KD-Tree
pcl::PointCloud<PointT> mls_points;   //输出MLS
pcl::MovingLeastSquares<PointT, PointT> mls;  // 定义最小二乘实现的对象mls
mls.setComputeNormals (false);  //设置在最小二乘计算中是否需要存储计算的法线
mls.setInputCloud (cloud_filtered);     //设置待处理点云
mls.setPolynomialOrder(2);          // 拟合2阶多项式拟合
mls.setPolynomialFit (false);  // 设置为false可以 加速 smooth
mls.setSearchMethod (treeSampling); // 设置KD-Tree作为搜索方法
mls.setSearchRadius (0.05); // 单位m.设置用于拟合的K近邻半径
mls.process (mls_points);       //输出

小白：师兄，这个代码里的KD-Tree是干嘛的？
师兄：Kd-Tree是一种数据结构，是空间二分树的一种特殊情况，可以很方便的用于进行范围搜索。在这里用KD-Tree就是为了便于管理、搜索点云，这种结构来可以很方便的找到最近邻点。
小白：原来如此，那上面mls.setSearchRadius (0.05) 的意思是不是就是搜索当前点以5cm为半径的空间中所有的点？
师兄：对的，然后把这些点用2阶多项式拟合~

小白：所以表面就变平滑啦！

如何估计点云的表面法线？

小白：师兄，现在可以网格化了吗？
师兄：还不行。。。别急，网格化前我们还需要估计一下点云的表面法线（normal）
小白：啊，怎么又冒出来一个法线。。。
师兄：法线好像是中学就学过了，应该还记得平面的法线的定义吧，平面的法线是垂直于该平面的向量，如下图所示

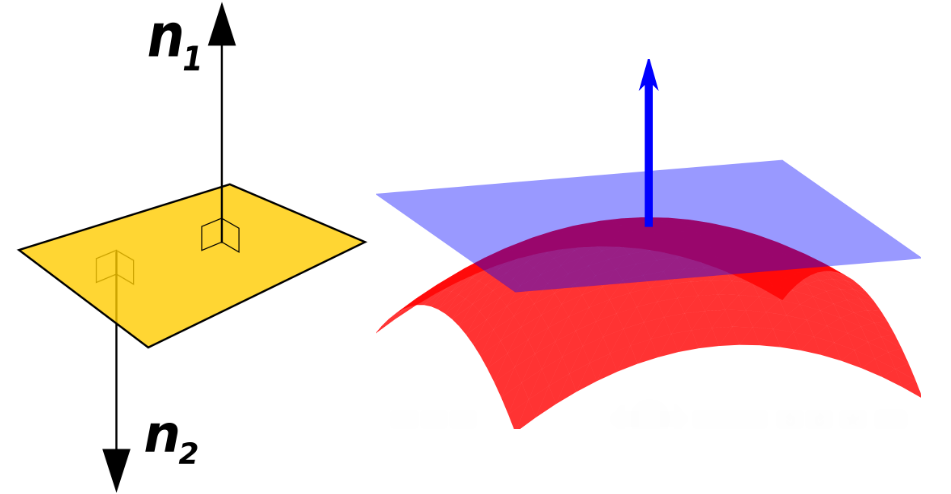
你看上面右边那个图，对于曲面来说，曲面在某点P处的法线为垂直于该点切平面（tangent plane）的向量
小白：记得呢，不过这个法线有什么用？怎么就突然冒出来了
师兄：法线很有用的，尤其是在三维建模中应用非常广泛，比如在计算机图形学（computer graphics）领域里，法线决定着曲面与光源（light source）的强弱处理（Flat Shading），对于每个点光源位置，其亮度取决于曲面法线的方向。
小白：原来如此。不过好像平面或曲面的法线比较容易计算，方程 ax + by + cz = d 表示的平面，向量(a, b, c)
就是其法线。而我们这里是点云呢！怎么算呢？
师兄：确实如此。点云的法线计算是稍微麻烦点，一般有两种方法：
1、使用曲面重建方法，从点云数据中得到采样点对应的曲面，然后再用曲面模型计算其表面的法线
2、直接使用近似值直接从点云数据集推断出曲面法线
这里主要用第2种方法来近似估计点云中每个点的表面法线。
具体来说，就是把估计某个点的表面法线问题简化为：从该点最近邻计算的协方差矩阵的特征向量和特征值的分析，这里就不多做介绍了。PCL已经帮我们封装好了函数啦
我们计算出来点云的法线大概是这样的

小白：那个箭头就代表法线吧？
师兄：对的，我们前面提到了，需要从该点的周围点邻域（也称为k邻域）估计一点处的表面法线，所以这个K邻域的选取也很关键
小白：这个K邻域选取会有什么影响吗？
师兄：有的，而且影响挺大的，K近邻的取值可以通过选择k个最近点，或者确定一个以r为半径的圆内的点集来确定，你看下面这个图是对同一个点云用不同尺度因子（k和r）进行法线估计的结果。左边部分表示比例因子选择的比较合适，估计的表面法线近似垂直于这两个平面，即使在互相垂直的边缘部分，也能明显看到边沿。而右边的尺度因子就选的有点大了，这样临近点集更大范围的覆盖临近表面的点，两个平面边沿处估计的法线就不准了，不能表达真实的情况。

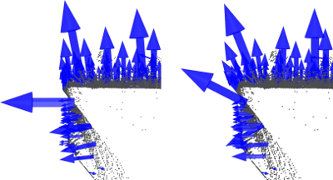
小白：确实是这样啊，看来编程的时候要格外注意了。
师兄：法线估计的示例如下，我也给你注释好啦

// 法线估计
pcl::NormalEstimation<PointT, pcl::Normal> normalEstimation;                    //创建法线估计的对象
normalEstimation.setInputCloud(cloud_smoothed);                                 //输入点云
pcl::search::KdTree<PointT>::Ptr tree(new pcl::search::KdTree<PointT>);         // 创建用于最近邻搜索的KD-Tree
normalEstimation.setSearchMethod(tree);
pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>);   // 定义输出的点云法线
// K近邻确定方法，使用k个最近点，或者确定一个以r为半径的圆内的点集来确定都可以，两者选1即可
normalEstimation.setKSearch(10);                    // 使用当前点周围最近的10个点
//normalEstimation.setRadiusSearch(0.03);           //对于每一个点都用半径为3cm的近邻搜索方式
normalEstimation.compute(*normals);                 //计算法线

本文参考：PCL官网

编程练习

前面我们已经介绍过点云滤波，这次练习主要是后续的平滑和法线估计，为后面网格化做铺垫。
题目：给定一个融合后的点云，已经对其进行下采样和滤波（代码已给）。请对其进行平滑（输出结果），然后计算法线，并讲法线显示在平滑后的点云上。
代码框架及待处理数据已经为你准备好了，公众号「计算机视觉life」后台回复：平滑，即可获得。
如果一切顺利，你将得到如下结果。你可以通过调整法线的稠密，放大查看法线计算的是否符合预期。

欢迎留言讨论，更多学习视频、文档资料、参考答案等关注计算机视觉life公众号，，菜单栏点击“知识星球”查看「从零开始学习SLAM」星球介绍，快来和其他小伙伴一起学习交流~