matlab根据输入响应求解传递函数

Posted 2022-04-14 studyer_domi

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了matlab根据输入响应求解传递函数相关的知识，希望对你有一定的参考价值。

被控对象的开环单位阶跃响应数据在文件matlab_work.mat中。在MATLAB指令窗中键入：

>> load matlab_work.mat

>> plot(t,y)

>> xlabel('t')

>> ylabel('y')

>> title('原始响应曲线')

在matlab中画出在输入为单位阶跃响应数据时输出随时间的变化曲线如下图所示：

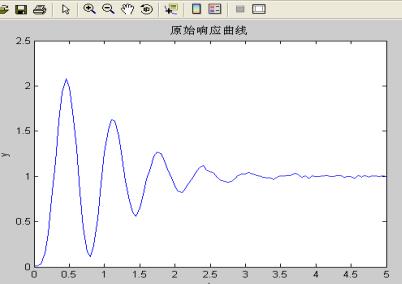
图1 被控对象的单位阶跃响应

2 系统模型的辨识

由于被控对象模型结构未知，题中仅给出了被控对象的单位阶跃响应。因此需要根据原始的数据分析得出原系统的基本结构。至于结构以及参数的最终确定，将使用MATLAB的系统辨识工具箱来实现。

2.1系统模型结构的估计

系统辨识工具箱提供的模型结构选择函数有struc、arxstruc和selstruc。

函数struc 生成arx结构参数，调用格式为：

nn＝struc (Na, Nb, Nk)

其中，Na、Nb 分别为arx模型多项式A(q)、B(q) 的阶次范围；Nk为arx模型纯滞后的大小范围；nn为模型结构参数集构成的矩阵。

函数arxstruc用来计算arx模型结构的损失函数，即归一化的输出预测误差平方和，调用格式为：

v＝arxstruc (ze, zv, nn)

其中，ze＝[y u]为模型辨识的I/O数据向量或矩阵。zv＝[yr ur]为模型验证的I/O数据向量或矩阵。nn为多个模型结构参数构成的矩阵，nn的每行都具有格式：nn＝[na nb nk]。v的第一行为各个模型结构损失函数值，后面的各行为模型结构参数。

函数selstruc 用来在损失函数的基础上进行模型结构选择，调用格式为：

[nn, vmod]＝selstruc (v, c)

其中v 由函数arxstruc获得的输出矩阵，为各个模型结构的损失函数。c为可选参数，用于指定模型结构选择的方式。

根据图2所示曲线的形状初步估测被控对象的模型应该为二阶系统或者更高阶系统。并且可以看出，纯滞后为0，故Nk恒为零。

在MATLAB指令窗中键入：

>> u=ones(size(y))

>> Z=[y,u]

>> v2=arxstruc(Z,Z,struc(2,0:2,0))

>> nn2=selstruc(v2,0)

>> v3=arxstruc(Z,Z,struc(3,0:3,0))

>> nn3=selstruc(v3,0)

>> v4=arxstruc(Z,Z,struc(4,0:4,0))

>> nn4=selstruc(v4,0)

>> v5=arxstruc(Z,Z,struc(5,0:5,0))

>> nn5=selstruc(v5,0)

>> v6=arxstruc(Z,Z,struc(6,0:6,0))

>> nn6=selstruc(v6,0)

>> v7=arxstruc(Z,Z,struc(7,0:7,0))

>> nn7=selstruc(v7,0)

>> v8=arxstruc(Z,Z,struc(8,0:8,0))

>> nn8=selstruc(v8,0)

得到如下结果：

nn2 = 2 2 0

nn3 = 3 1 0

nn4 = 4 1 0

nn5 = 5 5 0

nn6 = 6 2 0

nn7 = 7 1 0

nn8 = 8 1 0

于是，去除积分环节后的模型阶数为：二阶系统[2 1 0]、三阶模型[3 2 0]和四阶模型[4 1 0]，五阶系统模型为[5 5 0]，六阶系统模型为[6 2 0]，七阶系统模型为[7 1 0]，八阶系统模型为[8 1 0]。

2.2系统模型结构的确定

为了确定模型结构以及参数，使用MATLAB的系统辨识工具箱中已有的辨识函数arx()。辨识函数arx()的使用方法是：如果输入信号的列向量为u，输出信号的列向量为y，并选定了系统的分子多项式阶次m-1，分母多项式阶次n及系统的纯滞后d，则可以通过下面的指令辨识出系统的数学模型：

T=arx([y,u],[ n,m,d])

该函数将直接显示辨识的结果，且所得的T为一个结构体，其中T.A和T.B分别表示辨识得到的分子和分母多项式。由给定的观测数据建立系统数学模型后，还需要进行检验，看模型是否适用，如果不适用，则要修改模型结构，重新进行参数估计等。MATLAB的系统辨识工具箱中用于模型验证和仿真的函数主要有compare、resid、pe、predict 和idsim。此次实验主要用的是函数compare对模型进行验证。函数compare可将模型的预测输出与对象实际输出进行比较。验证过程与结果如下所示。

对二阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[2,3,0])

>> compare(M,Z)

得到结果如图2所示。

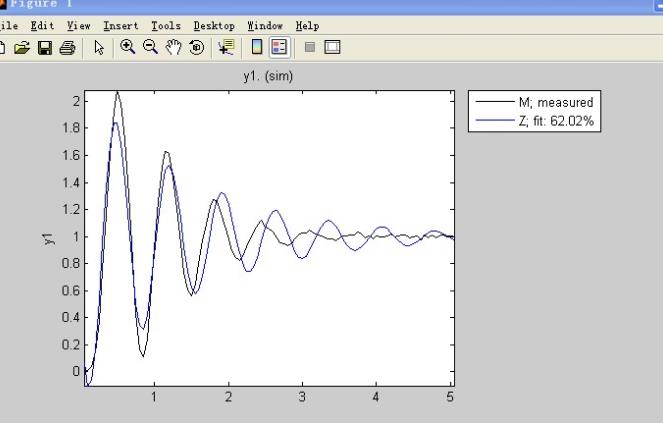图2 二阶模型的匹配结果

对三阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[2,4,0])

>> compare(M,Z)

得到结果如图3所示

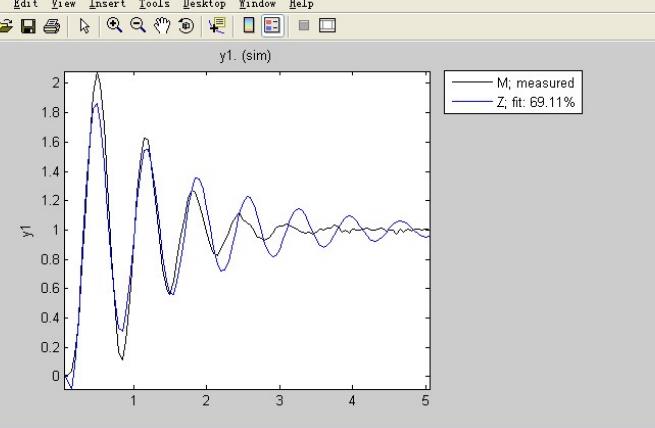
图3 三阶模型的匹配结果

对四阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[4,2,0])

>> compare(M,Z)

得到结果如图4所示

图4 四阶模型的匹配结果

对五阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[5,6,0])

>> compare(M,Z)

得到结果如图5所示

图5 五阶模型的匹配结果

对六阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[6,3,0])

>> compare(M,Z)

得到结果如图6所示

图6 六阶模型的匹配结果

对七阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[7,2,0])

>> compare(M,Z)

得到结果如图7所示

图7 七阶模型的匹配结果

对八阶系统的验证

在MATLAB指令窗中键入：

>> Z=iddata(y,u,0.05)

>> M=arx(Z,[8,2,0])

>> compare(M,Z)

得到结果如图8所示

图8 八阶模型的匹配结果

模型阶次的选取

从图2~8可以看出，八阶模型的拟合率已高达93%，符合要求。因此，为简便起见，不再选用更高阶系统，本次试验选用八阶系统模型。

在MATLAB指令窗中键入：

>> H=tf(M)

得到如下结果：

Transfer function from input "u1" to output "y1":

0.2012 z^8 + 0.2012 z^7

----------------------------------------------------------------------------------

z^8 - 1.082 z^7 - 0.1049 z^6 + 0.3345 z^5 + 0.1519 z^4 + 0.2915 z^3 + 0.02519 z^2

- 0.6381 z + 0.4242

Transfer function from input "v@y1" to output "y1":

0.0161 z^8

----------------------------------------------------------------------------------

z^8 - 1.082 z^7 - 0.1049 z^6 + 0.3345 z^5 + 0.1519 z^4 + 0.2915 z^3 + 0.02519 z^2

- 0.6381 z + 0.4242

Input groups:

Name Channels

Measured 1

Noise 2

Sampling time: 0.05

上述模型为离散时间系统模型，为了得到连续时间系统模型，在MATLAB指令窗中键入：

>> G=d2c(H(1))

得到如下结果：

Transfer function from input "u1" to output "y1":

0.2012 s^8 + 10.33 s^7 + 1133 s^6 + 4.305e004 s^5 + 1.764e006 s^4 + 4.255e007 s^3 + 7.547e008 s^2 + 8.042e009 s

+ 4.182e010

----------------------------------------------------------------------------------------------------------------

s^8 + 17.15 s^7 + 4570 s^6 + 5.992e004 s^5 + 4.939e006 s^4 + 4.392e007 s^3 + 9.317e008 s^2 + 3.74e009 s

+ 4.177e010

Input groups:

Name Channels

Measured 1

2.3传递函数模型系数的修正

得到了系统传递函数，对其使用阶跃响应step命令，并与原数据线对比，看是否吻合。命令如下：

plot(t,y,'red');

hold on;

step(G)

得到的结果：

图9 修正后的曲线匹配

从上图可以看出，由arx模型得到的传递函数的阶跃响应曲线并不能与原始数据线很好的拟合。故考虑在该传递函数的基础上，对其系数修改。

考虑忽略传递函数分子的高次项

G=tf([8.042e009 4.182e010],[ 1 17.15 4570 5.992e004 4.939e006 4.392e007 9.317e008 3.74e009 4.177e010]);

plot(t,y,'red');

hold on

step(G)

图10 忽略高次项后的曲线匹配

由上图看到，忽略高次项对系统的阶跃响应并无多大影响，但是使系统结构简化，在此基础上继续对传递函数的系数做修改。

调整系统的零点。

由于系统零点的作用为减小峰值时间，使系统响应速度加快，并且零点越接近虚轴，这种作用越显著。但对分子常数项的修改，则会影响到系统的收敛值，较麻烦，故考虑只对分子一次项的系数进行修改。经过多次尝试，最后得到的系统传递函数如下：

G=tf([4.255e007 4.182e010],[ 1 17.15 4570 5.992e004 4.939e006 4.392e007 9.317e008 3.74e009 4.177e010]);

plot(t,y,'red');

hold on

step(G)

图11 调整零点后的曲线匹配

即得到最终的系统传递函数为：

Transfer function:

4.255e007 s^3 + 4.182e010

---------------------------------------------------------------------------------------------------------------------------------------

s^8 + 17.15 s^7 + 4570 s^6 + 5.992

计算数据匹配率：

计算公式：FIT=100(1-norm(Y-YHAT)/norm(Y-mean(Y))) (in %)

代码如下：

yhat=step(G,t);

num=norm(y-yhat,2);

ym=mean(y);

ymean=y;

ymean(:)=ym;

den=norm(y-ymean,2);

fit=100*(1-num/den)

得出数据匹配率为：fit =91.8822满足要求。

与50位技术专家面对面

20年技术见证，附赠技术全景图

以上是关于matlab根据输入响应求解传递函数的主要内容，如果未能解决你的问题，请参考以下文章

Matlab中fsolve传递系数变量

matlab用龙格库塔法求解变系数常微分方程

如何利用matlab求相关系数？

matlab GUI设计，在两个edit中分别输入分子和分母的系数，点击按钮在edit3中显示结果

数字信号处理线性常系数差分方程 ( 使用 matlab 求解 “ 线性常系数差分方程 “ 示例 | A 向量分析 | B 向量分析 | 输入序列分析 | matlab 代码 )