如何用matlab求解logistic模型

Posted 2023-03-23

t=[0,30,45,76]

p=[2200,4000,8260,10000]
p=L/(1+(L/P0-1)e^(-rt))

希望求解出L,p0,r
并画出预测图形

logistic模型属于非线性问题。所以求解其模型函数的系数可以用nlinfit（）非线性回归分析函数来解决。由于给出的数据偏少，通过有效的插值方法，增加合理的数据点。主要代码：

a0=[-35.287，813.17，0.0098613];

t=0:5:75; %t=[0,30,45,76];

p=[2200 2259.2 2429.3 2699.5 3058.7 3495.8 4000 5228.9 7048.4 8260 8738.6 9152.7 9494 9754.1 9924.9 9997.9]; %p=[2200,4000,8260,10000];

fun=@(a,t)a(1)./(1+(a(1)/a(2)-1)*exp(-a(3).*t));

a= nlinfit(t,p,fun,a0);

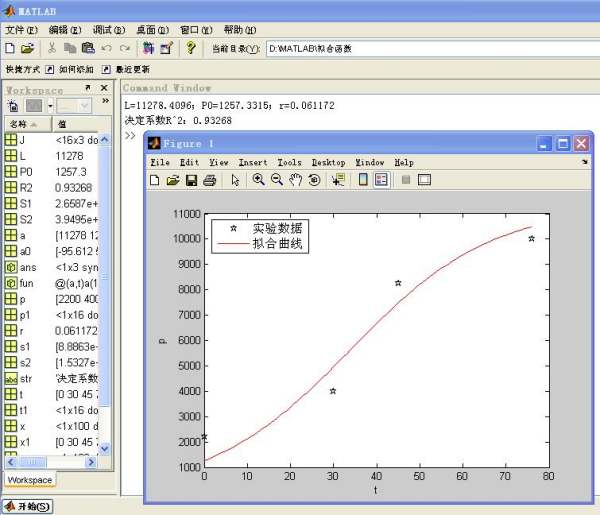
运行结果

L=11278.4096；P0=1257.3315；r=0.061172

决定系数R²：0.93268

参考技术A 建立m函数文件存为logistic1
function f=logistic1(b)
t=[0,5,10,24,33,48,57,72,96,120,144,168,192,216];y=[0,0.028,0.103,0.336,0.450,0.597,0.716,0.778,0.835,0.849,0.816,0.839,0.811,0.816];
f = y-b(1)./(1+b(2).*exp(-b(3).*t));

b0=[10,2,2];
>> b=leastsq('logistic1',b0)
b =

0.8221 13.9173 0.0818

或者cftool
General model:
f(x) = b/(1+a*exp(-k*x))
Coefficients (with 95% confidence bounds):
a = 13.92 (6.301, 21.53)
b = 0.822 (0.7911, 0.853)
k = 0.08184 (0.06479, 0.0989)

Goodness of fit:
SSE: 0.01404
R-square: 0.9898
Adjusted R-square: 0.9879
RMSE: 0.03572

怎么用matlab求解Logistic模型中的三个参数

给你这个实例，来说明如何用matlab求解Logistic模型中的三个参数。

x=[21 24 27 30 33 36 39 42 45 48];  %已知数值

y=[0 4.5541 11.5836 19.9043 22.7024 25.2441 26.2109 26.5693 26.6396 25.9511]; %已知数值

fun=inline('a(1)./(1+exp(a(2)-a(3).*x))','a','x');  %定义Logistic模型函数

a0=[0.95717  0.48538  0.80028]; %a的初值

a = nlinfit(x,y,fun,a0);  %求解Logistic模型中的三个参数

syms x

fx=vpa(fun(a,x),5);

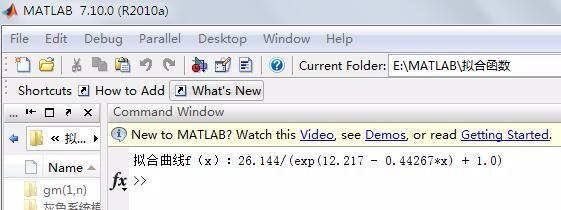
str1=['拟合曲线f（x）：',char(fx)];

fprintf('%s\\n',str1)  %显示Logistic模型函数

运行结果

参考技术A 建立m函数文件存为logistic1
function f=logistic1(b)
t=[0,5,10,24,33,48,57,72,96,120,144,168,192,216];y=[0,0.028,0.103,0.336,0.450,0.597,0.716,0.778,0.835,0.849,0.816,0.839,0.811,0.816];
f = y-b(1)./(1+b(2).*exp(-b(3).*t));
b0=[10,2,2];
>> b=leastsq('logistic1',b0)
b =
0.8221 13.9173 0.0818
或者cftool
General model:
f(x) = b/(1+a*exp(-k*x))
Coefficients (with 95% confidence bounds):
a = 13.92 (6.301,21.53)
b = 0.822 (0.7911,0.853)
k = 0.08184 (0.06479,0.0989)
Goodness of fit:
SSE:0.01404
R-square:0.9898
Adjusted R-square:0.9879
RMSE:0.03572