聚类的外部指标(Purity, ARI, NMI, ACC) 和内部指标(NCC,Entropy,Compactness,Silhouette Index)，附代码 (Python 和 Matlab)

Posted 2023-03-20 阿卡西番茄酱

聚类性能评估的外部指标和内部指标，附代码 (Python 和 Matlab)

文章目录

• 聚类性能评估的外部指标和内部指标，附代码 (Python 和 Matlab)
• • 1 外部指标
  • • 1.1 Purity
    • • 原理解释
      • Python代码
      • Matlab代码
    • 1.2 ARI
    • • 原理解释
      • Python 代码
      • Matlab 代码
    • 1.3 NMI
    • • 原理解释
      • Python 代码
      • Matlab代码
    • 1.4 ACC
    • • Python 代码
      • Matlab 代码
  • 2 内部指标
  • • 2.1 Internal and external validation measures (NCC)
    • • 原理解释
      • Python 代码
      • Matlab 代码
    • 2.2 Entropy
    • • 原理解释
      • Python 代码
      • matlab代码
    • 2.3 Compactness
    • • 原理解释
      • Python 代码
      • Matlab 代码
    • 2.4 Silhouette Index
    • • 原理解释
      • Python 代码
      • Matlab 代码
  • 总结

众所周知，聚类有效性指标，包括外部指标和内部指标，对于评价聚类结果的质量非常有用。

1 外部指标

1.1 Purity

原理解释

先给出Purity的计算公式：

首先解释一下，为什么需要引入纯度计算，因为聚类中总是会出现此类与标签对应的类不一致，虽然他们表示的数字都是1，但是实质内容可能不一致。

用一个例子说明，例子借用了博客评价聚类的指标：纯度、兰德系数以及调整兰德系数 - 简书

详细请见上述我附上的链接地址~

Python代码

def purity(labels_true, labels_pred):
    clusters = np.unique(labels_pred)
    labels_true = np.reshape(labels_true, (-1, 1))
    labels_pred = np.reshape(labels_pred, (-1, 1))
    count = []
    for c in clusters:
        idx = np.where(labels_pred == c)[0]
        labels_tmp = labels_true[idx, :].reshape(-1)
        count.append(np.bincount(labels_tmp).max())
    return np.sum(count) / labels_true.shape[0]

Matlab代码

function [purity] = Purity(labels_true, labels_pred)
clusters = unique(labels_pred);
labels_true = labels_true';
labels_pred = labels_pred';
labels_true = labels_true(:);
labels_pred = labels_pred(:);
count = [];

for c = 1:length(clusters)
	idx = find(labels_pred == c);
	temp = labels_true(idx);
	labels_tmp = reshape(temp,1,length(temp(:)));
	T=tabulate(labels_tmp);
	count = [count, max(T(:,2))];
end
purity = sum(count)/size(labels_true,1);
end

感谢Redmor提供的matlab代码~

1.2 ARI

原理解释

参考博客 调整兰德系数（Adjusted Rand index，ARI）的计算_的图表~

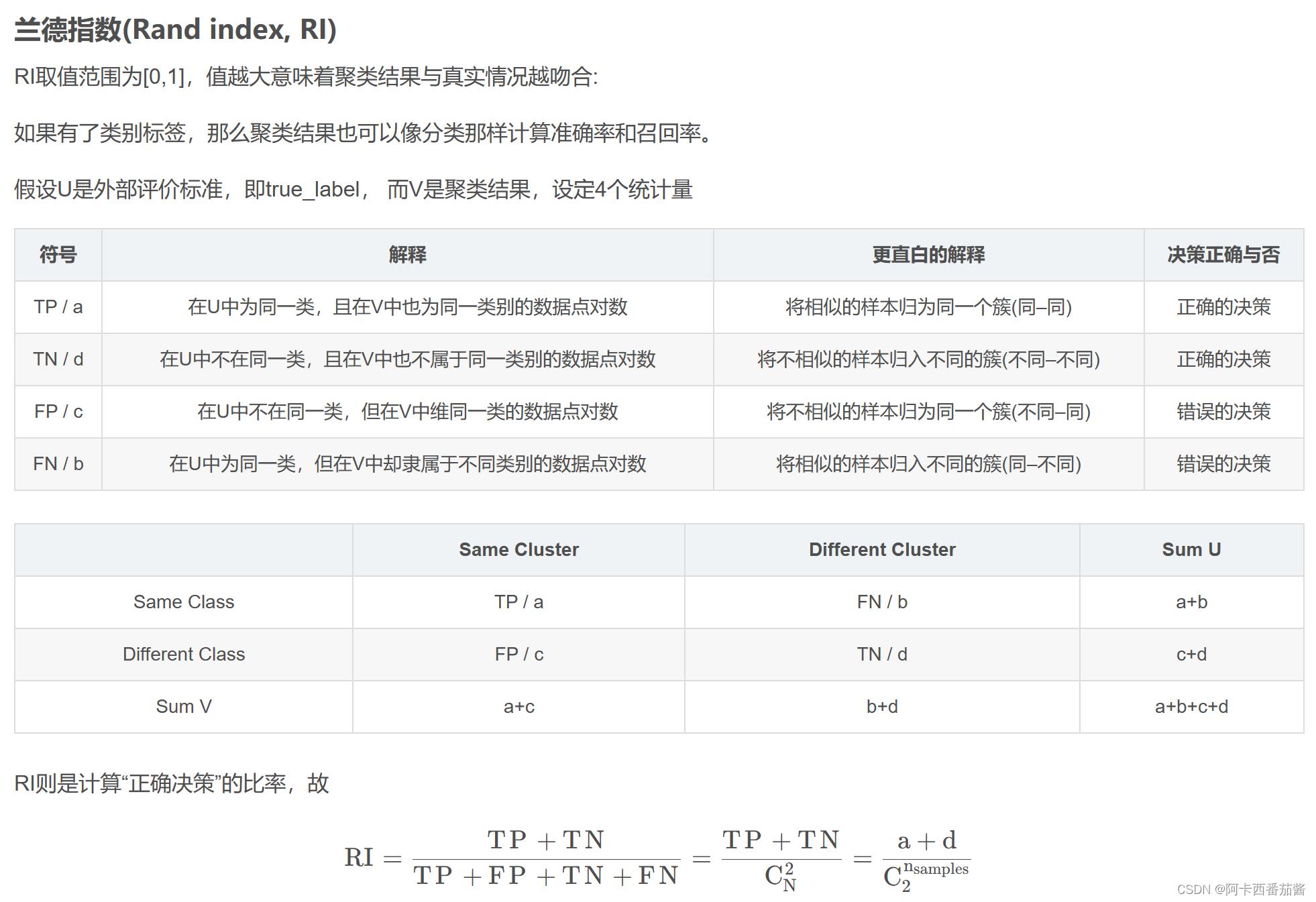
但是由于RI无法保证随机划分的聚类结果的RI值接近于0，所以现在主流科研工作者，使用的外部指标偏向于ARI，更加客观。

ARI的改进如下：

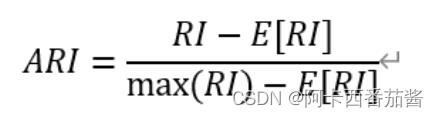
取值为[-1,1]，绝对值越大效果越好~注意是绝对值噢。

Python 代码

def ARI(labels_true, labels_pred, beta=1.):
    from sklearn.metrics import adjusted_rand_score
    ari = adjusted_rand_score(labels_true, labels_pred)

    return ari

Matlab 代码

function ri = Eva_ARI(p1, p2, varargin)
%RAND_INDEX Computes the rand index between two partitions.
%   RAND_INDEX(p1, p2) computes the rand index between partitions p1 and
%   p2.
%
%   RAND_INDEX(p1, p2, 'adjusted'); computes the adjusted rand index
%   between partitions p1 and p2. The adjustment accounts for chance
%   correlation.

% Parse the input and throw errors
    adj = 0;
    if nargin == 0
    end
    if nargin > 3
        error('Too many input arguments');
    end
    if nargin == 3
        if strcmp(varargin1, 'adjusted')
            adj = 1;
        else
            error('%s is an unrecognized argument.', varargin1);
        end
    end
    if length(p1)~=length(p2)
        error('Both partitions must contain the same number of points.');
    end
    
	% Preliminary computations and cleansing of the partitions
    N = length(p1);
    [~, ~, p1] = unique(p1);
    N1 = max(p1);
    [~, ~, p2] = unique(p2);
    N2 = max(p2);
    
    % Create the matching matrix
    for i=1:1:N1
        for j=1:1:N2
            G1 = find(p1==i);
            G2 = find(p2==j);
            n(i,j) = length(intersect(G1,G2));
        end
    end
    
    % If required, calculate the basic rand index
    if adj==0
        ss = sum(sum(n.^2));
        ss1 = sum(sum(n,1).^2);
        ss2 =sum(sum(n,2).^2);
        ri = (nchoosek2(N,2) + ss - 0.5*ss1 - 0.5*ss2)/nchoosek2(N,2);
    end
    
    
    % Otherwise, calculate the adjusted rand index
    if adj==1
        ssm = 0;
        sm1 = 0;
        sm2 = 0;
        for i=1:1:N1
            for j=1:1:N2
                ssm = ssm + nchoosek2(n(i,j),2);
            end
        end
        temp = sum(n,2);
        for i=1:1:N1
            sm1 = sm1 + nchoosek2(temp(i),2);
        end
        temp = sum(n,1);
        for i=1:1:N2
            sm2 = sm2 + nchoosek2(temp(i),2);
        end
        NN = ssm - sm1*sm2/nchoosek2(N,2);
        DD = (sm1 + sm2)/2 - sm1*sm2/nchoosek2(N,2);
        ri = NN/DD;
    end 
    

    % Special definition of n choose k
    function c = nchoosek2(a,b)
        if a>1
            c = nchoosek(a,b);
        else
            c = 0;
        end
    end
end

hungarian函数可以直接去matlab中文社区获取噢或者后台私信我~

1.3 NMI

原理解释

MI, NMI, AMI（互信息，标准化互信息，调整互信息

大家可以参考这一篇博客，讲的很详细~

我就简单附上代码啦

Python 代码

def NMI_sklearn(predict, label):
    # return metrics.adjusted_mutual_info_score(predict, label)
    return metrics.normalized_mutual_info_score(predict, label)

Matlab代码

function z = Eva_NMI(x, y)
assert(numel(x) == numel(y));
n = numel(x);
x = reshape(x,1,n);
y = reshape(y,1,n);
l = min(min(x),min(y));
x = x-l+1;
y = y-l+1;
k = max(max(x),max(y));
idx = 1:n;
Mx = sparse(idx,x,1,n,k,n);
My = sparse(idx,y,1,n,k,n);
Pxy = nonzeros(Mx'*My/n);
Hxy = -dot(Pxy,log2(Pxy));
Px = nonzeros(mean(Mx,1));
Py = nonzeros(mean(My,1));
Hx = -dot(Px,log2(Px));
Hy = -dot(Py,log2(Py));
MI = Hx + Hy - Hxy;
z = sqrt((MI/Hx)*(MI/Hy));
z = max(0,z);

感谢开源社区~

1.4 ACC

精确度计算，有一点值得提醒，Python是直接与标签对比，没有进行Mapping步骤，适用于分类结果评估；matlab进行了Mapping步骤适用于聚类结果评估。

Python 代码

def AC(labels_true, labels_pre):
    acc = accuracy_score(labels_true, labels_pre)
    # acc = np.sum(labels_true==labels_pre) / np.size(labels_true)
    return acc

Matlab 代码

function [accuracy, ConMtx] = Eva_CA(dataCluster,dataLabel)

nData = length( dataLabel );
nC = max(dataLabel);
E = zeros( nC, nC );
for m = 1 : nData
    i1 = dataCluster( m );
    i2 = dataLabel( m );
    E( i1, i2 ) = E( i1, i2 ) + 1;
end
ConMtx=E';
E=-E;
[C,~]=hungarian(E);
nMatch=0;
for i=1:nC
    nMatch=nMatch-E(C(i),i);
end

accuracy = nMatch/nData;

以上外部指标均是目前科研工作者常用指标。

2 内部指标

与外部有效性指数相比，内部有效性指数评价的是数据分区的聚类结构，目的是衡量一个集群内聚类对象的比例，评估聚类对象的分布，而没有外部信息的支持。这里外部信息指原始数据的标签。

2.1 Internal and external validation measures (NCC)

原理解释

NCC 测量的是簇内距离和簇间距离的组合。簇内距离是指一个簇内物体之间的距离。作者将两个对象的 “群内协议”（Sintra）定义为两个对象之间的属性数量和群内距离之差。

距离的测量方法如下：

如果比较的所有属性值之间存在匹配，则drs=0，否则rs= N ⁄ 1，其中N是这两个对象之间在比较过程中发现的不匹配（mismatches）数量。

簇间距离 （Dinter），是不属于同一簇的两个对象（rands）之间的距离，也就是说，这个距离可以测量两个簇之间的距离。

NCC 的表达式是针对任何聚类过程的结果而定义的，其中 T 对应于聚类中心的数量。

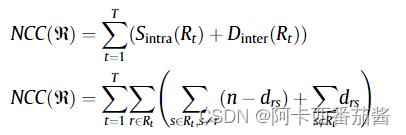
当然，NCC 度量也可以用二进制矩阵 Y 来表示，如果对象（rands）属于同一个聚类，则 yrs=1，否则 yrs=0。NCC(Y) 公式用二进制矩阵表示：

通过NCC的度量，可以观察到集群内（Sintra）和集群间（Dinter）距离之间的关系。根据作者的说法，当群内距离值较小时，群内距离就会增加。另外，当簇间距离增加时，聚类过程中的群组彼此之间变得更加异质化，即集群之间更加不相似。如果这种相似度（Sintra）和距离（Diner）增加，NCC的值就会趋于增加，否则NCC值就会减少。

Python 代码

def NCC(label, x):
    m = x.shape[0]
    n = x.shape[1]
    Y = np.zeros((m, m))
    for r in range(m):
        for s in range(m):
            if label[r] == label[s]:
                Y[r, s] = 1

    drs = np.zeros((m, m))
    for r in range(m):
        for s in range(m):
            for att in range(n):
                if x[r, att] != x[s, att]:
                    drs[r, s] += 1

    ncc = 0.0
    for r in range(m):
        for s in range(m):
            if r != s:
                ncc += (n - 2 * drs[r, s]) * Y[r, s] + drs[r, s]

    return ncc

Matlab 代码

function ncc = NCC_Y(Cluster_lable,x,n)

%%%Eq.(33)
% n is the number of attributes (categorical).
[m,~] = size(x);
Y = zeros(m,m);
for r = 1:m
    for s = 1:m
        if Cluster_lable(r) == Cluster_lable(s)
            Y(r,s) = 1;
        end
    end
end

drs = zeros(m,m);
for r = 1:m
    for s = 1:m
        for att = 1:n
            if x(r,att) ~= x(s,att)
                drs(r,s) = drs(r,s) + 1;
            end
        end
    end
end

ncc = 0;
for r = 1:m
    for s = 1:m
        if r~= s
            ncc = ncc + (n - 2*drs(r,s))*Y(r,s) + drs(r,s);
        end
    end
end

注释表示论文中的公式，参考文献附文末。

2.2 Entropy

原理解释

香农熵是在2001年提出的，用于计算数据集无序性的方法。应用于聚类的方法，如果一个簇数据尽可能地有序是否可以说明，更适合聚为一类呢？基于此，有学者Rˇezanková (2009)提出使用熵来计算一个集群中属性的无序性。

p(u)lt ：u表示属性l中某一个可能的值，t表示一个簇，p(u)lt表示，在簇t中在l属性上拥有u值的频率。

Entropy值越小，代表聚类效果越好~

Python 代码

def Entropy(label, x):
    m = x.shape[0]
    n = x.shape[1]
    k = len(np.unique(label))
    # 每一个属性可能出现的值
    no_values = []
    for i in range(n):
        no_values.append(len(np.unique(x[:, i])))

    # cluster 成员数
    num_in_cluster = np.ones(k)
    for i in range(m):
        num_in_cluster[label[i]] += 1

    # p_u_lt
    P = []
    for t in range(k):
        # mt
        tp = np.where(label == t)[0]
        p_u_l = []
        for l in range(n):
            p_u_lt = []
            for u in range(no_values[l]):
                belong_lt = np.where(x[tp][:, l] == u)[0]
                p_u_lt.append(len(belong_lt) / len(tp))
            p_u_l.append(p_u_lt)
        P.append(p_u_l)

    # H
    H = np.zeros(k)
    for t in range(k):
        H_lt = np.zeros(n)
        for l in range(n):
            H_lt_u = np.zeros(no_values[l])
            for u in range(no_values[l]):
                if P[t][l][u] != 0:
                    H_lt_u[u] = - P[t][l][u] * np.log(P
        
                

                    
                    


 
文章目录
 
前言
纯度(purity)
纯度的计算Python代码
  
标准互信息(NMI)
熵
互信息
标准互信息
MI 和 NMI的计算实现 Python 版
  
调整互信息(AMI)
示例代码
  
兰德系数(Rand Index)
示例代码
  
调整兰德系数(Adjusted Rand index)
示例代码
 

 
前言
 
本文主要介绍聚类算法的一些常见评测指标。
 
假设某一种算法得到聚类结果为:
 
$$\mathrm{A}=\left[\begin{array}{lllllllllcccccccc}1& 2& 1& 1& 1& 1& 1& 2& 2& 2& 2& 3& 1& 1& 3& 3& 3\end{array}\right]$$
 
标准的聚类结果为：
 $$\mathrm{B}=\left[\begin{array}{llllllllccccccccc}1& 1& 1& 1& 1& 1& 2& 2& 2& 2& 2& 2& 3& 3& 3& 3& 3\end{array}\right]$$
 
那么如何评价该算法的聚类效果？
 
纯度(purity)
 
把每个簇中最多的类作为这个簇所代表的类，然后计算正确分配的类的数量，然后除以总数：
 
 
纯度计算如下：
 
$$\text{ purity }=\frac{(\text{ cluster }A+\text{ cluster }B+\text{ cluster }C)}{\text{ total }}=\frac{(4+5+4)}{18}=0.722$$
 
一般而言，纯度随着clusters数量的增加而增加。例如，将每个样本结果分为一个单独的簇，此时纯度为1。鉴于此，不能简单用纯度来衡量聚类质量与聚类数量之间的关系。
 
纯度的计算Python代码
 
def purity(result, label):
    # 计算纯度

    total_num = len(label)
    cluster_counter = collections.Counter(result)
    original_counter = collections.Counter(label)

    t = []
    for k in cluster_counter:
        p_k = []
        for j in original_counter:
            count = 0
            for i in range(len(result)):
                if result[i] == k and label[i] == j: # 求交集
                    count += 1
            p_k.append(count)
        temp_t = max(p_k)
        t.append(temp_t)
    
    return sum(t)/total_num
 
标准互信息(NMI)
 
熵
 
标准互信息(Normalized mutual information, NMI)这个指标源自信息论，所以需要先了解熵(entropy)的概念。熵这个概念是用于量化不确定性，熵的定义如下：
 $$H(p)=-\sum _i{p}_i{\log }_2\left(p_i\right)$$
 
其中$P_i$表示label为$i$的概率。延续上述示例，可以计算其熵。
 class A ： 6 / 18
 class B ：7 / 18
 class C ：5 / 18
 
$$\text{ entropy}=-\left(\left(\frac{6}{18}\right)\cdot \log \left(\frac{6}{18}\right)\right)-\left(\left(\frac{7}{18}\right)\cdot \log \left(\frac{7}{18}\right)\right)-\left(\left(\frac{5}{18}\right)\cdot \log \left(\frac{5}{18}\right)\right)$$
 其值为 1.089。需要注意的是：当类别或标签分布均匀时，熵值比较高。
 
熵随着不确定性的减小而减小。假设我们有两个类，其中类A中有9个数据点，类B中有1个数据点。在这种情况下，如果我们要预测一个随机选择的数据点的类别，我们会比之前的情况更确定。这是因为此时熵计算如下，结果值为0.325：
 $$\text{ entropy }=-\left(\left(\frac{9}{10}\right)\cdot \log \left(\frac{9}{10}\right)\right)-\left(\left(\frac{1}{10}\right)\cdot \log \left(\frac{1}{10}\right)\right)$$
 
以上即为熵的概念。
 
互信息
 
互信息是用以衡量数据分布之间的相关性。互信息越高，相关性也越高。两个离散随机变量 $X$ 和 $Y$的互信息定义如下：
 
$$MI(X,Y)=\sum _{x=1}^{|X|}\sum _{y=1}^{|Y|}P(x,y)\log (聚类算法指标整理$$
 聚类算法指标整理
 聚类任务介绍
 多标签外部聚类评估指标的 NMI 和 B3 等效项
 Kmeans
 机器学习——聚类算法的评估指标