力扣每日一题——NO.33——搜索旋转排序数组

Posted 2022-02-17 东条希尔薇

原题链接

题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

例如：

【4,5,6,7,0,1,2】目标：0，返回值：4

要求：时间复杂度O(logn)

思路求解

我们看到了时间复杂度为logn，自然想到了可以使用二分查找算法

但是数组并不是完全有序的，所以我们不能直接套用二分查找，我们需要把这个算法进行一下改进：

我们可以发现，如果我们将数组进行二分的话，那么一定是有一个半区间是有序的（显然易见）

所以我们可以先把数组划分成两个区间

然后分别判断两个区间是否有序：（nums[0]<nums[mid]则证明左区间有序因为数组在某区间是基本严格单调递增的，反之则说明右区间有序）

最后，我们只需要检索一下目标值是否在我们的递增区间内即可

如果存在，则缩小查找目标在这个区间内，反之，选择另外一个区间

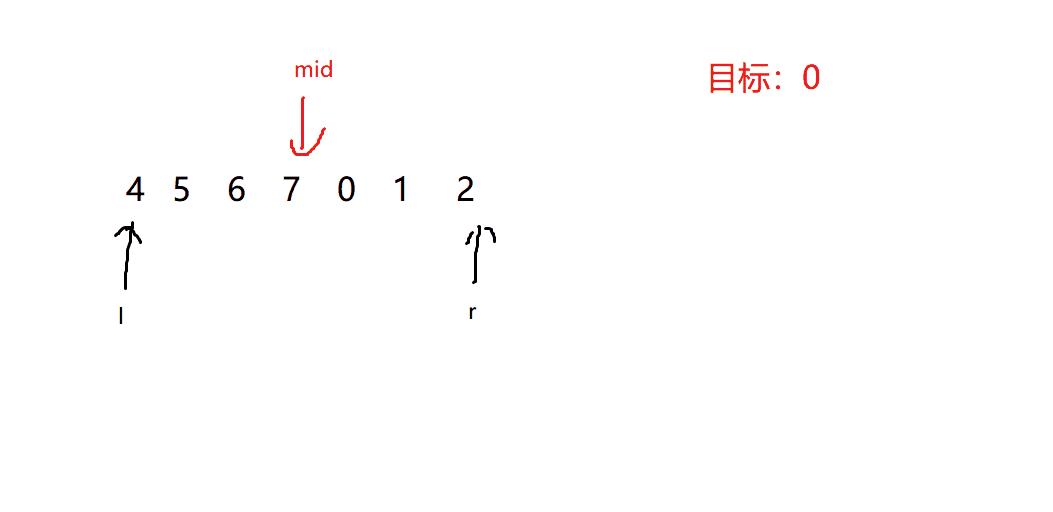
代码实现

class Solution 
public:
    int search(vector<int>& nums, int target) 
        int l=0;
        int n=nums.size();
        int r=n-1;
        if(n==0||(n==1&&nums[0]!=target))
        
            return -1;
        

        if(n==1&&nums[0]==target)
        
            return 0;
        
        //以前都是对于数组没有元素，或只有一个元素的数组进行处理

        while(l<=r)
        
            int mid=(((r-l)>>1)+l);
            if(nums[mid]==target)
            
                return mid;//缩小到中点，找到了元素
            
            if(nums[0]<=nums[mid])//此判断条件表示左区间有序，对左区间进行处理
            
                if(nums[0]<=target&&target<nums[mid])//观察目标值是否在这个范围内，如果在，则将目标缩小在这个区间
                
                    r=mid-1;
                
                else
                
                    l=mid+1;
                
            

            else
            
                if(nums[mid]<target&&target<=nums[n-1])
                
                    l=mid+1;
                
                else
                
                    r=mid-1;
                
            

        
        return -1;//没有找到元素，l和r错开了
    
;