使用TensorFlow实现余弦距离/欧氏距离（Euclidean distance）以及Attention矩阵的计算

Posted 2023-02-19 liuchongee

最近在使用tensorflow完成句子相似度建模等任务时常常会用到各种距离的计算，而且有很多论文提出了Attention机制，所以这里就介绍一下如何使用tensorflow实现上述各种功能。
这里首先假定我们的输入是两个四维的Tensor，然后我们需要计算的是其中某个维度的距离。比如说我们的输入是batch个句子，句长是sent_len, 每个词被表示成embed_size的词向量。所以我们的输入就是一个[batch_size, sent_len, embed_size, 1]的Tensor，需要计算的就是两个句子的Attention矩阵。Aij表示句子1中第i个单词和句子2中第j个单词的距离（余弦距离，欧氏距离，L1距离等），也就是计算两个长度为embed_size的向量之间的距离。
为了方便表示和调试，我们这里使用shape为[2,3,4,1]的Tensor来表示上述句子。

1，Euclidean distance

欧氏距离很简单，以向量为例（x1, x2, x3,….,xn），（y1, y2, y3,….,yn），那么其欧氏距离的计算公式如下图所示：

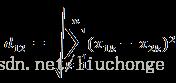
在tensorflow中如何实现呢，代码如下：

import tensorflow as tf

x3 = tf.constant([[[[1], [2], [3], [4]],
                   [[5], [6], [7], [8]],
                   [[9], [10], [11], [12]]],

                  [[[1], [2], [3], [4]],
                   [[5], [6], [7], [8]],
                   [[9], [10], [11], [12]]]], tf.float32)

x4 = tf.constant([[[[3], [4], [1], [2]],
                   [[5], [7], [8], [6]],
                   [[9], [12], [11], [10]]],

                  [[[1], [2], [3], [4]],
                   [[5], [6], [7], [8]],
                   [[9], [10], [11], [12]]]], tf.float32)

with tf.Session() as sess:
    dis = sess.run(tf.square(x3-x4))
    dis1 = sess.run(tf.reduce_sum(tf.square(x3-x4), 2))
    euclidean = sess.run(tf.sqrt(tf.reduce_sum(tf.square(x3-x4), 2)))
    print dis, dis1, euclidean

这部分代码实现的功能是：我们有x3，x4两个输入，每个有两句话，每句话有三个单词。计算的是对应单词之间的距离。下面是输出：

dis：
[[[[ 4.]
   [ 4.]
   [ 4.]
   [ 4.]]

  [[ 0.]
   [ 1.]
   [ 1.]
   [ 4.]]

  [[ 0.]
   [ 4.]
   [ 0.]
   [ 4.]]]


 [[[ 0.]
   [ 0.]
   [ 0.]
   [ 0.]]

  [[ 0.]
   [ 0.]
   [ 0.]
   [ 0.]]

  [[ 0.]
   [ 0.]
   [ 0.]
   [ 0.]]]] 
dis1：
[[[ 16.]
  [  6.]
  [  8.]]

 [[  0.]
  [  0.]
  [  0.]]] 

Euclidean：
[[[ 3.99999976]
  [ 2.44948959]
  [ 2.82842684]]

 [[ 0.        ]
  [ 0.        ]
  [ 0.        ]]]

所以Euclidean距离的计算方法就是：

euclidean = tf.sqrt(tf.reduce_sum(tf.square(x3-x4), 2))

余弦距离

跟Euclidean距离相似，余弦距离也可以用来表征两个向量之间的相似度。其计算公式如下图所示：

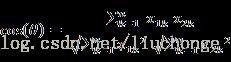
在tensorflow中实现方法如下，这里我们仍然沿用x3，x4的定义，之写出sess.run()部分的代码：

with tf.Session() as sess:
    #求模
    x3_norm = tf.sqrt(tf.reduce_sum(tf.square(x3), axis=2))
    x4_norm = tf.sqrt(tf.reduce_sum(tf.square(x4), axis=2))
    #内积
    x3_x4 = tf.reduce_sum(tf.multiply(x3, x4), axis=2)
    cosin = x3_x4 / (x3_norm * x4_norm)
    cosin1 = tf.divide(x3_x4, tf.multiply(x3_norm, x4_norm))
    a, b, c, d, e = sess.run([x3_norm, x4_norm, x3_x4, cosin, cosin1])
    print a, b, c, d, e

上述代码按照cosine的计算公式进行分步求解。最终的到了两个句子对应词之间的余弦距离。从结果会看出cosin和cosin1是一样的。结果如下所示：

x3_norm:
[[[  5.47722483]
  [ 13.19090366]
  [ 21.11871338]]

 [[  5.47722483]
  [ 13.19090557]
  [ 21.11871147]]] 
x4_norm:
[[[  5.47722483]
  [ 13.19090366]
  [ 21.11871338]]

 [[  5.47722483]
  [ 13.19090557]
  [ 21.11871147]]] 
x3_x4:
[[[  22.]
  [ 171.]
  [ 442.]]

 [[  30.]
  [ 174.]
  [ 446.]]] 
cosin:
[[[ 0.73333353]
  [ 0.98275894]
  [ 0.99103123]]

 [[ 1.00000024]
  [ 1.00000012]
  [ 1.00000012]]] 
cosin1:
[[[ 0.73333353]
  [ 0.98275894]
  [ 0.99103123]]

 [[ 1.00000024]
  [ 1.00000012]
  [ 1.00000012]]]

Attention矩阵计算

如上面提到的那样，Attention矩阵A中的每个元素Aij表示句子1中第i个单词和句子2中第j个单词的距离。那么如何实现呢。我们先介绍一种比较简单的思路：

def input_attention(x1, x2):
    #将每个句子按单词进行切分
    x1_unstack = tf.unstack(x1, axis=1)
    x2_unstack = tf.unstack(x2, axis=1)
    D = []
    for i in range(len(x1_unstack)):
        d = []
        for j in range(len(x2_unstack)):
        #计算两个单词之间的相似度距离
            dis = tf.sqrt(tf.reduce_sum(tf.square(x1_unstack[i]- x2_unstack[j]), axis=1))
            d.append(dis)
        D.append(d)
    D1 = tf.reshape(D, [2, 3, 3])
    D2 = tf.reshape(tf.transpose(D, perm=[2, 0, 1, 3]), [2,3,3])
    return D1, D2
with tf.Session() as sess:
    A, A1 = input_attention(x3, x4)
    a, a1 = sess.run([A, A1])
    print a, a1

这种方法是先将句子进行unstack，也就是“分词”。经过下面这行命令我们就得到了3个[2, 4, 1]的tensor。即3个单词

x1_unstack = tf.unstack(x1, axis=1)

所以下面这条命令之后我们就得到一个[2, 1]的tensor。在经过两个循环（3×3），我们就获得了[3, 3, 2, 1]的tensor。D是一开始我用的，当时觉得是没问题的，但是经过调试发现，他返回的结果是错误的，因为D是[3,3,2,1]，2在最里面，reshape时不会被直接调到外面。结果如下所示：

dis = tf.sqrt(tf.reduce_sum(tf.square(x1_unstack[i]- x2_unstack[j]), axis=1))

A:
[[[  4.           0.           8.36660004]
  [  8.          16.24807739  16.        ]
  [  8.94427204   8.           2.44948983]]

 [[  0.           8.48528099   8.        ]
  [ 16.4924221   16.           8.36660004]
  [  8.           2.82842708   0.        ]]] 
A1:
[[[  4.           8.36660004  16.24807739]
  [  8.94427204   2.44948983   8.48528099]
  [ 16.4924221    8.36660004   2.82842708]]

 [[  0.           8.          16.        ]
  [  8.           0.           8.        ]
  [ 16.           8.           0.        ]]]

根据上面的结果，我们很明显可以看出A1才是我们想要的数据。