余弦相似度和欧氏距离
Posted codehome
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了余弦相似度和欧氏距离相关的知识,希望对你有一定的参考价值。
Basic Vector Space Search Engine Theory
LA2600– January2, 2004 - presented by Vidiot
Overview:
A Vector Space Search Engine uses very simple techniques from matrix algebra to compare documents based on word frequency.
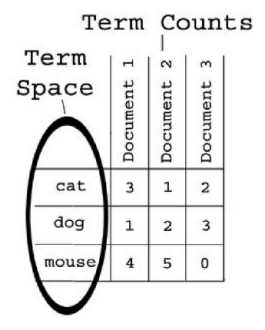
The first major component of a vector space search engine is the concept of a term space. Simply put, a term space consists of every unique word that
appears in a collection of documents.
The second major component of a vector space search engine is term counts.
Term counts are simply records of how many times each term occurs in an
individual document. This is usually represented as a table, as in the illustration below.
By using the term space as a coordinate space, and the term counts as
coordinates within that space, we can create a vectorfor each document. In
order to understand how we create these vectors, let’s look at a simple example. You’re probably familiar with Cartesian Coordinates; plotting points along X, Y,
and Z axes. Similarly, in the case of a term space containing three unique terms we would refer to these axes as the term1, term2, and term3axes. (In vector
space search theory these axes are usually referred to as dimensions.) By
counting how many times each term appears in a document, and plotting the
coordinates along each term dimension, we can determine a point in the term
spacethat corresponds to the document. Using this point we can then create a
vector for the document back to the origin.
Once we have plotted the vector of a document through the term space, we can then calculate the magnitude of the vector. Think of the magnitude as the length of the line between the documents point in the term space and the origin of the
term space(at coordinates(0,0,0) in our example). These vector magnitudes will allow us to compare documents by calculating the cosign of the angle between
them. For example, identical documents will have a cosign of1, documents
containing similar terms will have positive decimal cosigns, and documents with
nothing in common will have cosigns of zero.
A Simple Example:
In this tutorial we’ll go through the entire indexing and search process using a simple three dimensional example that is easy to envision.
To begin, lets assume we have a collection of three documents. Each document contains combinations of the words cat, dog, and mouse. The words cat, dog,
and mouse are the term space. Thus we can say that each document has coordinates along the cat, dog, and mousedimensions. These coordinates are
determined by how many times each term appears in the document. For example, document 1 below would have a “cat-dog-mouse vector” of (3,1 ,4).
We calculate the magnitude of the vector for each document using the Pythagorean
Theorem, but in this case we have more than
V1 = (32)+(12)+(42)= 9+1 +16= 26=5.09901
V2 = (12)+(22)+(52) = 1 +4+25= 30=5.47722
V3 = (22)+(32)+(02)= 4+9+0 = 15=3.87298
NOTE: The two vertical bars on each side of the vector variable mean “the magnitude of”.
Note that the Pythagorean Theorem formula will continue to apply no matter how many dimensions we are working with. For example, if we had a term space with
Also, the astute observer may have noticed that different documents can have the exact same vector magnitudes. For example, two different documents with vectors of (1,2,3) and (3,2,1) would both have a vector magnitude of 3.74165. This is not a contradiction. As we will see, relevancy scores of documents are based on the dimensionality of the query term that is searched for, thus documents with identical vector magnitudes can return very different query results. In other words, just because two lines are the same length, it doesn’t necessarily mean that they are pointing to the same angle within the term space.
Querying :
To query the document collection index, we project the vector of our query into the vector space, and then calculate the cosign of the angle between the query and each of the other documents in the collection. In English, this means we project the query vector into the vector space, and then see what other document vectors are nearby.
For example, if the query term is “mouse”, then the “cat-dog-mouse vector” would be (0,0,1). The magnitude of our query vector would then be:
NOTE: A simple optimization while coding is to check if the query term is in the term
space, and if so, then Q will always = 1 , but this only works with a single search
term. For multiple search terms, count how many are within the term space, and take the square root of the count. Because query terms are not represented as values less than 1 , the solution to Q will always be the square root of a whole number. But this assumes that each term appears only once in each query, which is not necessarily a
good assumption because of word stemming which I will discuss shortly.
To calculate the cosign between the query and a document vector, we divide the Dot Productof the query vector and the document vector, by the magnitude of the query vector multiplied by the magnitude of the document vector.
Q * V1_ Q x V1
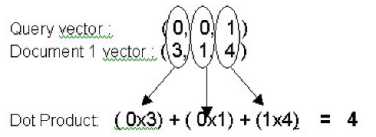
The Dot Productis the sum of the term counts for each document and the
corresponding query term counts multiplied together. For example, if we were to search for the term “mouse”, the coordinates for the Query would be (0,0,1)
because the words cat and dog do not appear and the word mouse appears
once is the third dimension of the term space. Document 1 in our example
collection would have a vector of (3,1 ,4) based on the term counts listed in the
table above. If we wanted to calculate the Dot Product between the Query and
Document 1 we would make the following calculation:
Now we divide the Dot Product of 4, by the product of the query and document magnitudes, to get the cosine value. As we saw earlier the magnitude of the
vector of Document 1 is 5.09901 , and the magnitude of the Query vector = 1 . Thus the cosign value is 4 divided by 5.09901 .
Let’s try it out. The cosign of the angle between the query for “mouse”, and Document 1 would be calculated by:
Q * V1 Q x V1
= (0x3)+(0x1)+(1x4) = 4 = 0.78446
1 x 5.09901 5.09901
NOTE: If a document doesn’t contain any relevant search terms from the query, the Dot Productwill be zero, because zero divided by any value is still zero, thus the cosign will also be zero. This is good to remember while writing efficient code.
If we performed this calculation for the other two documents we would get the following cosigns:
Doc 1 = 0.78446 Doc 2 = 0.91287 Doc 3 = 0.00000
By arranging the documents in descending order according to the cosigns, as so:
Doc 2 = 0.91287 Doc 1 = 0.78446 Doc 3 = 0.00000
…we can see that document 2 is the most relevant to the query of “mouse”, and a quick glance at our term counts table above will confirm this. Document 1 is
slightly less relevant, and Document 3 is completely irrelevant, because it doesn’t contain any instances of the word “mouse”.
An easy way to think of this is that the closer the cosign value is to 1 , the more relevant the document is. If the cosign is zero, then the documents are
The process of indexing a collection is specific to the type of documents being
indexed. Vector Space search technology can be used on any type information that can be represented in a structured fashion, so it will work equally well on
text, images, cryptographic keys, or even DNA. However, custom parsers must be constructed to handle the information in a regulated fashion, and can often be
First each html document must be pre-processed, and then indexed as part of a collection. (Collections can only be indexed as a whole. Adding additional files to a collection after it has been indexed changes the dimensionality of the term
space and negates the stored document vector magnitudes.)
We begin by stripping out all the HTML content because is contains no semantic content. We can also strip out any formatting such as line breaks and carriage returns so that we are left with a simple block of text.
Next, we remove stop words from the text. Stop words are words that occur
commonly in the English language, but don’t add any semantic value to the text as a whole. For example, words like “the”, “and”, “of”, and “or” are irrelevant to
the actual semantic meaning of the document but would artificially enlarge the
term space, and thus the processing time, if they were left in. Also adverbs such as “quickly” (or anything typically ending in “ly”) can be removed because they
don’t add any additional semantic value.
Next, we stemthe remaining terms in the document. Stemming consists of
reducing English word to their root word forms. For example, the words “runner”, “running”, and “runs” would all be stemmed to the word “run.” The Porter
Stemming Algorithm is typically used for this purpose. This further reduces the
term space while maintaining semantic content.
After we have finished with these three steps we are left with (hopefully) the
minimal number of terms required to contain the semantic meaning of the original document.
No we can begin indexing the collection by building the term space and calculating the vector magnitude of each document.
step1 step2 step3 step4

Step 1 – Strip out HTML, punctuation, and line breaks to leave only blocked textual
content.
Step 2 – Remove stop words (such as “the”) to reduce the size of the term space.
Step 3 – Stem the remaining terms to further reduce the size of the term space while
maintaining semantic content. For example, “runner” and “running” will both be
stemmed to “run”. The Porter stemming algorithm is commonly used for this purpose. Step 4A – Populate the term space with one unique instance of each term, from every
document, that spans across the entire collection so that all possible terms are included. Store the results.
Step 4B – Count and record how many times each relevant term appears in each
document.
Step 4C – Calculate and record the vector magnitude, Vn , for each document.
NOTE: It is important to keep in mind that how the parser divides up information will affect the search results. For example, if you were indexing the contents of a book, the indexing time and search results would differ greatly depending on
whether you broke the text up by chapter, page, or paragraph. You will need to
First, it is VERY calculation intensive, and therefore quite slow. Because of all
the floating-point mathematics, it requires lots and lots of processor time, which
kills performance. High performance requires large systems with code optimized to run calculations exclusively in RAM. Hopefully, this will become less of a
barrier as processor speeds continue to increase.
Second, dynamic collections will (usually) require re-indexing each time a new document is added. This is because every time you introduce a new term into the term space, you are adding another dimension to the matrix, and all existing documents must be re-indexed so that their vectors are relevant to the new
dimensionality. This is perhaps the most serious barrier to the widespread
adoption of this technology because it makes real time availability of search
results next to impossible.
Third, it requires additional mathematical transformation of the collection matrix in order to detect additional connections between documents with Latent Semantic Indexing. LSI allows us to find additional connections between documents on a semantic level. It is outside the scope of this document, but it is an important
next-step in Vector Space search technology, and another barrier to real time
usability.
Resources and Additional Reading
- http://www.perl.com/pub/a/2003/02/19/engine.html - Excellent article about
以上是关于余弦相似度和欧氏距离的主要内容,如果未能解决你的问题,请参考以下文章