余弦距离和欧氏距离，知道原理和公式后真的很简单

Posted 2022-01-14 振华OPPO

余弦距离

我们来看下公式，其实就是余弦计算公式：A和B是两个任意向量，除以它们模的乘积，就得到它们夹角的余弦值，其中向量Ai和Bi是向量A和B的每一个分量。

简单来说，余弦相似度，就是计算两个向量间的夹角的余弦值。

余弦距离就是用1减去这个获得的余弦相似度。

余弦值取值范围为[-1,1]，余弦距离取值范围为[0,2]，这样就满足了非负性的性质。

是不是很简单~

欧式距离

欧式距离我们从初中或者说小学就开始使用了，就是计算距离空间中的两点的实际距离。

这里的p为点(x1,y1)与点(x2,y2)之间的欧氏距离，当然扩展到多维空间中，公式就拓展到：

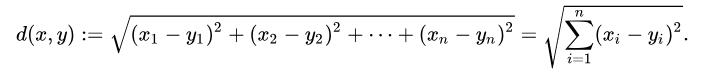
是不是更简单~

选择依据

总体来说，欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。

1. 统计两部剧的用户观看行为，用户A的观看向量为(0,1)，用户B为(1,0)；此时二者的余弦距很大，而欧氏距离很小；我们分析两个用户对于不同视频的偏好，更关注相对差异，显然应当使用余弦距离。

2. 而当我们分析用户活跃度，以登陆次数(单位：次)和平均观看时长(单：分钟)作为特征时，余弦距离会认为(1,10)、(10,100)两个用户距离很近；但显然这两个用户活跃度是有着极大差异的，此时我们更关注数值绝对差异，应当使用欧氏距离。