漫步最优化四十二——Partan法

Posted 2023-02-17 会敲键盘的猩猩

$\\textbf漆黑的冷空中有你，$
$\\textbf惺忪的眼睛中有你，$
$\\textbf心底的记忆中有你，$
$\\textbf你留在我的脑海中，$
$\\textbf一直这么挥之不去。$
$\\textbf无论哪时哪刻，$
$\\textbf心中都想着你的笑，$
$\\textbf想着你到我侧相拥，$
$\\textbfI can dream about you.$
$\\textbf——畅宝宝的傻逼哥哥$

在早期的最优化中，对于两变量函数来说，用最速下降法得出的解轨迹表征出zig-zag模式。对于某些性质较好的函数，相邻的解差不多组成两条线，他们在最小值的邻域内相交，如图1所示，因此比较明显的策略是连接初始点与第二个解，沿着这个方向执行最速下降法。对于凸二次函数，在 $n$次迭代内就能收敛，这个方法也被称为parallel tangent法或着partan法，这是因为在二次函数的情况下，所得轮廓的正切属性。


图1

Partan算法如图2所示，假设初始点为$\\mathbfx_0$，并利用两次最速下降法得到点 $\\mathbfx_1,\\mathbfy_1$，然后沿着 $\\mathbfy_1-\\mathbfx_1$方向进行线搜索得到点 $\\mathbfx_2$，这就完成了第一次迭代。对于第二次迭代，对点 $\\mathbfx_2$执行最速下降得到点 $\\mathbfy_2$，沿着 $\\mathbfy_2-\\mathbfx_1$方向得到点 $\\mathbfx_3$，一直重复此过程。从效果上看，图2中的点 $\\mathbfy_1,\\mathbfy_2,\\ldots$是通过最速下降法得到的而 $\\mathbfx_2,\\mathbfx_3,\\ldots$是沿着方向 $\\mathbfy_2-\\mathbfx_1,\\mathbfy_3-\\mathbfx_2,\\ldots$方向用线搜索得到的。


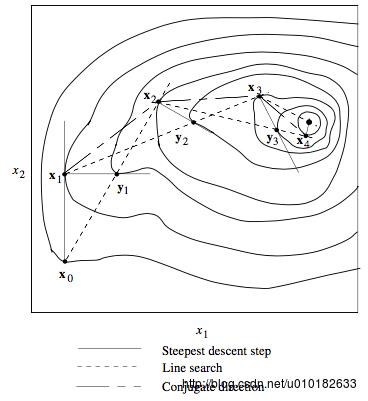
图2

对于凸二次问题，连接 $\\mathbfx_1,\\mathbfx_2,\\ldots,\\mathbfx_k$的线组成一个共轭梯度方向集，可以通过以下方法来证明：先假设 $\\mathbfd_0,\\mathbfd_1,\\ldots,\\mathbfd_k-1$是共轭梯度方向集，然后说明 $\\mathbfd_k$是 $\\mathbfd_0,\\mathbfd_1,\\ldots,\\mathbfd_k-1$的共轭梯度方向。

考虑图3所示的步骤，注意到

gTkdi=0漫步最优化四十——Powell法(上)

漫步最优化四十——Powell法(上)

漫步最优化四十一——Powell法(下)

漫步最优化四十一——Powell法(下)

漫步最优化三十二——最速下降法

漫步最优化四十三——拟牛顿法