离散数学中传递闭包怎么求 通俗一点

Posted 2023-04-04

离散数学中传递闭包怎么求 通俗一点

方法：warshall法，即运行n次，每次使得MR[n][i],MR[i][n]都为1时使得MR[i][j]为1,否则还是为MR[i][j]。

传递闭包的计算过程一般可以用Warshell算法描述： 

For 每个节点i Do
For 每个节点j Do
If j能到i Then
For 每个节点k Do
a[j, k] := a[j, k] Or ( a[j, i] And a[ i, k] ) 

其中a数组为布尔数组，用来描述两个节点是否相连，可以看做一个无权图的邻接矩阵。算法过程跟Floyd很相似，三重循环，枚举每个中间节点。不过传递闭包只需要求出两个节点是否相连，而不用求其间的最短路径长。

传递性：对于一个节点i，如果j能到i，i能到k，那么j就能到k。求传递闭包，就是把图中所有满足这样传递性的节点都弄出来，计算完成后，就知道任意两个节点之间是否相连。 

传递闭包的定义：R’是R（不具有传递性质）变动最少的步骤得到的具有传递性质的关系。

扩展资料

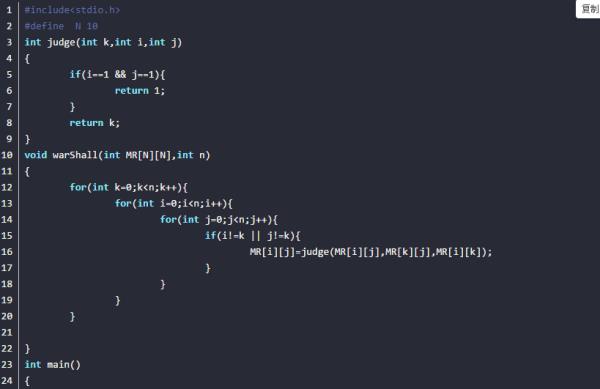
算法实例：

#include<stdio.h>

#define  N 10 

int judge(int k,int i,int j)

if(i==1 && j==1)

return 1;

return k;

void warShall(int MR[N][N],int n)

for(int k=0;k<n;k++)

for(int i=0;i<n;i++)

for(int j=0;j<n;j++)

if(i!=k || j!=k)

MR[i][j]=judge(MR[i][j],MR[k][j],MR[i][k]);

 

int main()

int MR[10][10];

int mul;

scanf("%d",&mul);

for(int i=0;i<mul;i++)

for(int j=0;j<mul;j++)

scanf("%d",&MR[i][j]);

printf("求传递闭包为:\\n");

warShall(MR,mul);

for(int i=0;i<mul;i++)

for(int j=0;j<mul;j++)

printf("%d ",MR[i][j]);

printf("\\n");

return 0;

运行结果：

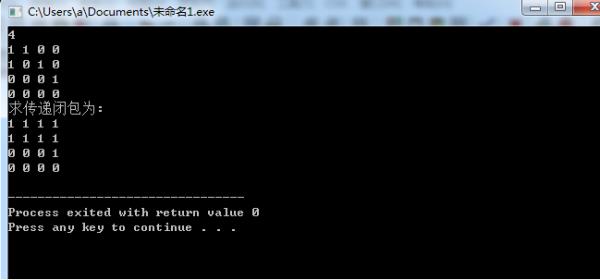
参考资料：百度百科-传递闭包

参考技术A 传递闭包就是反复求矩阵的幂，直到结果不再变化为止。
从矩阵上，如何观察和判断传递性，可以这样做：
http://jingyan.baidu.com/article/ea24bc399a9cbcda63b3316d.html本回答被提问者和网友采纳 参考技术B 因为∅∪∅=∅
所以∀n∅ⁿ=∅
t(∅)=∪∅ⁿ=∅

t(R)=∪Rⁿ
(t(R))²=∪R²ⁿ ⊆ ∪Rⁿ
⋮
(t(R))ⁿ=∪Rⁿⁿ ⊆ ∪Rⁿ
从而t(R)∪(t(R))²∪(t(R))³⋯
=∪Rⁿ
即t(t(R))=∪Rⁿ = t(R)

(离散数学)输入一个关系矩阵,用C语言编程求出它的自反闭包,对称闭包和传递闭包

其中传递闭包要求用两种方法实现
不好意思小弟刚进来,分不够,还请哪位高手帮个忙

参考技术A 我用面向对象写的 自己改一下

#include<iostream.h>
template<class T>
void Warshall( T *a , int m , int n )

int i = 0,j = 0;
for( i = 0 ; i < n ; i++ )

for( j = 0 ; j < m ; j++ )

if( a[j][i] == 1 )

int k = 0;
for( int x = 0 ; x < n ; x++ )

a[j][k] = a[j][k] || a[i][k];
k++;





for( i = 0 ; i < m ; i++ )

for( j = 0 ; j < n ; j++ )

cout << a[i][j] << '\t';

cout<<endl;


void main()

int ai[4][4] = 0,1,0,0 , 1,0,1,0 , 0,0,0,1 , 0,0,0,0 ;
Warshall(ai,4,4);