李宏毅深度学习笔记——呕心整理版

Posted 2022-12-19 _Elf_

李宏毅深度学习笔记——呕心整理版

闲谈叨叨叨:

之前看过吴恩达的一部分课程，所以有一定理论基础，再看李宏毅的课程会有新的理解。我先以有基础的情况写完学习过程，后续再以零基础的角度补充细节概念（估计不会啦，因为懒~）。长篇预警！可以慢慢看。多数只是自己的笔记，不会太有语言的概念解释，建议自己看一遍视频（往后字可能会越来越多，听我慢慢叨咕吧）。笔记只是提供回忆、巩固理解的工具。若有问题，欢迎评论讨论，有时间我会改正哒！

经过我多年学习经验（没有啦~），预习真的很重要，其实更多是重复记忆，加深理解。我的建议是先看吴恩达的课程了解机器学习和深度学习的基本知识框架和概念，还有理论推导，理解就可以，这就相当于预习；然后看李宏毅的课程，换个思路，以实际应用加深理解，就会感觉吴恩达的课程缘由不太清楚的自然而然就通了；看李宏毅的课程同时，看刘二大人的pytorch课程，动手操作，学会后完成李宏毅的作业；pytorch需要线性代数和概率论（这些课上要好好学，忘了的可以速学一下考研课程）以及python基础，我会整理一些推荐课程和学习路线。

关于李宏毅课程的视频顺序，我大多是先看2021年，用2022年视频作为补充，快速过一遍，选修部分也看。视频链接还有一位大佬整理的资源我会附在正文的引入部分。

目录附上：

文章目录

• 李宏毅深度学习笔记——呕心整理版
• • 1 引入
  • • 1.1 机器学习&深度学习
    • 1.2 课程规划
    • 1.3 机器学习例子
    • • 1.3.1 训练过程（training）
      • 1.3.2 改进（很牛逼，建议有基础后回看）
      • 1.3.3 激活函数
      • 1.3.4 神经网络Neural Network
    • 1.4 深度学习简介
    • • 1.4.1 反向传播（back propagation）
      • 1.4.2 回归 Regression
      • 1.4.3 分类（classification）
      • 1.4.4 逻辑回归（Logistic Regression）
    • 1.5 Homework
  • 2 优化分析
  • • 2.1 局部最小值（local minima）与鞍点（saddle point）
    • 2.2 批次（Batch）与动量（Momentum）
    • 2.3 自动调整学习率 (Learning Rate)
    • 2.4 损失函数（Loss）也会有影响
    • 2.5 批次标准化（Batch Normalization）
    • 2.6 深度学习
  • 3 卷积神经网络（CNN）
  • • 3.1 卷积神经网络（CNN)
    • 3.2 Spatial Transformer Layer
  • 4 自注意力机制（Self-attention）
  • • 4.1 引入
    • 4.2 self-attention
    • 4.3 Multi-head Self-attention
  • 5 Transformer

正片开始：

1 引入

• 视频资料整理：李宏毅2021&2022机器学习
• 视频：2022-机器学习相关规定

1.1 机器学习&深度学习

机器学习就是寻找一个复杂函数。

深度学习的函数就是类神经网络。

• 函数的输入可以是向量、矩阵、序列等等；
• 函数的输出可以是数值（称为regression 回归）、类别（classification 分类）、文本、图片等等

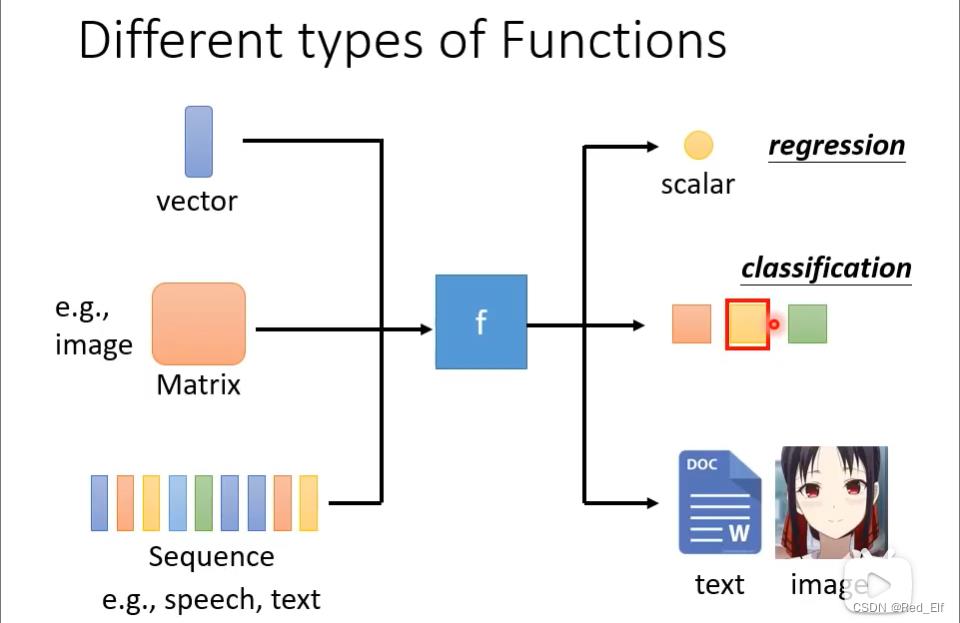
回归 regression：

分类 classification：

structured learning：

1.2 课程规划

——————————先更新到前5章——————————

Lecture1-5： Supervised Learning 监督学习

训练数据要有标注，数据集要知道输出值

缺点：耗费人工

Lecture 7： Self-supervised Learning

无标注资料——Pre-train

Lecture 6： Generative Adversarial Network（GAN）

Lecture 12： Reinforcement Learning（RL）强化学习

不知道怎么标注

Lecture 8： Anomaly detection 异常检测

Lecture 9： Explainable AI 可解释性AI

Lecture 10： Model attack 模型攻击

Lecture 11： Domain adaptation 域适应

Lecture 13： Network Compression

Lecture 14： life-long learning

Lecture 15： Meta learning

1.3 机器学习例子

• 传送门：
  • （上）机器学习基本概念简介
  • （下）机器学习基本概念简介

根据过往观看次数预测明天的观看次数

1.3.1 训练过程（training）

1. 含有未知参数的函数
   

2. 定义损失函数
   

   标签 label：已知的对应结果

   求出$e_1$到$e_N$
   $$Loss:L=\frac{1}{N}\sum _n{e}_n$$

   补充：
   loss函数可自己定义，以下常见三类：MAE、MSE、交叉熵
   

   误差曲面（error surface）：

   

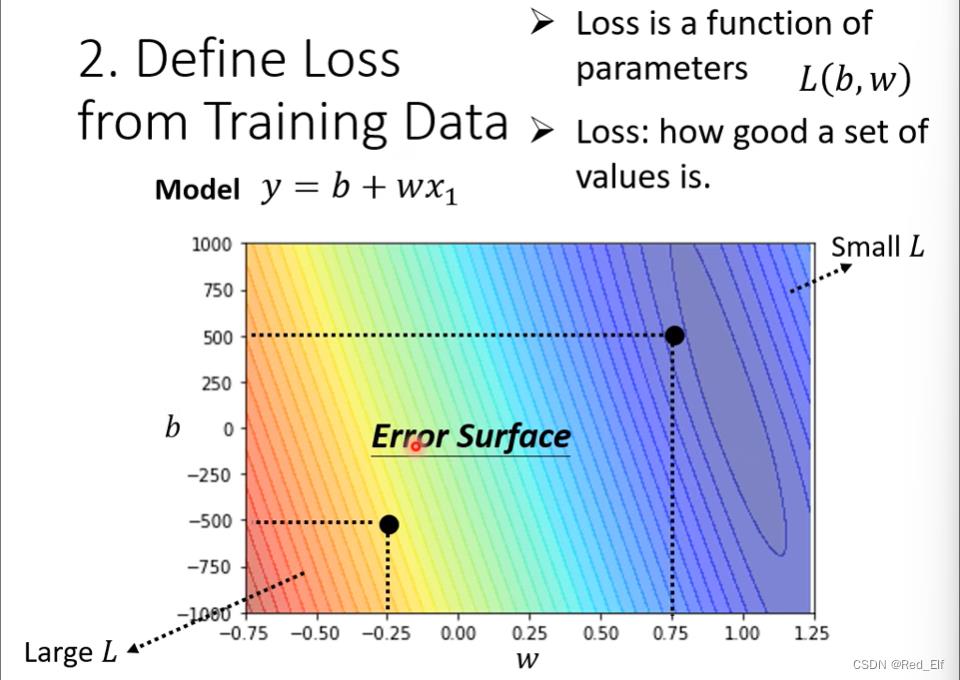
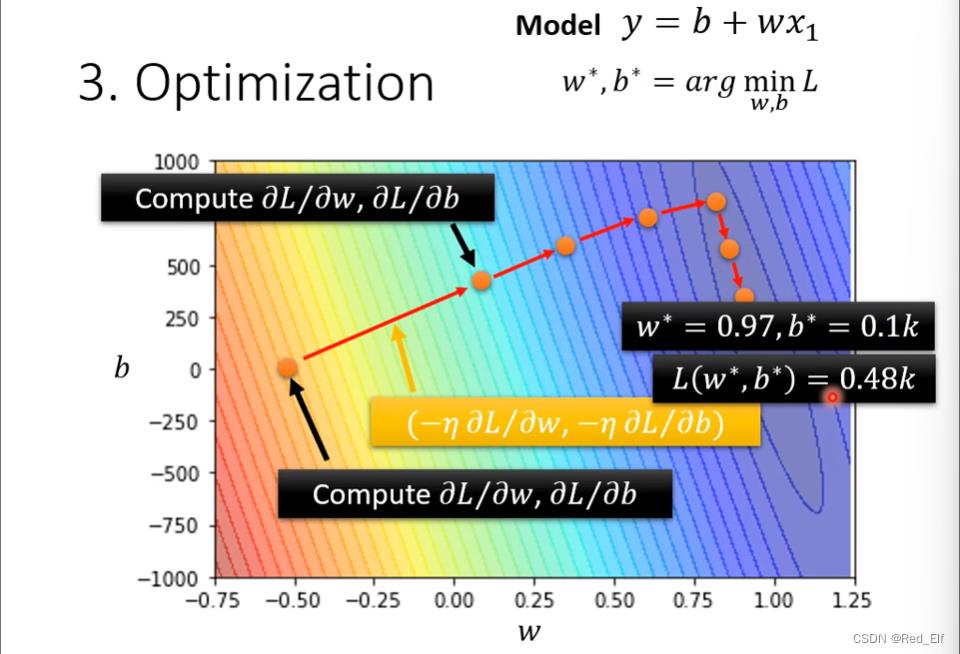
3. 优化
   $$w^{\ast },b^{\ast }=arg\underset{w,b}{\min }L$$

   $argmin$：使后面的公式最小的参数

   梯度下降 gradient descent

   假设只有$w$一个参数

   

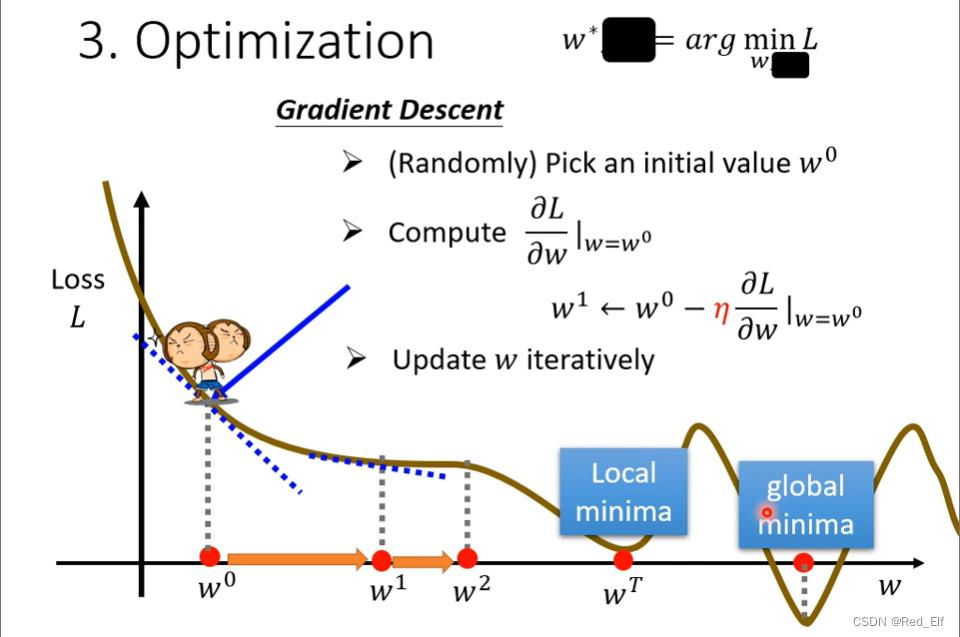
   带上$b$嘞

   

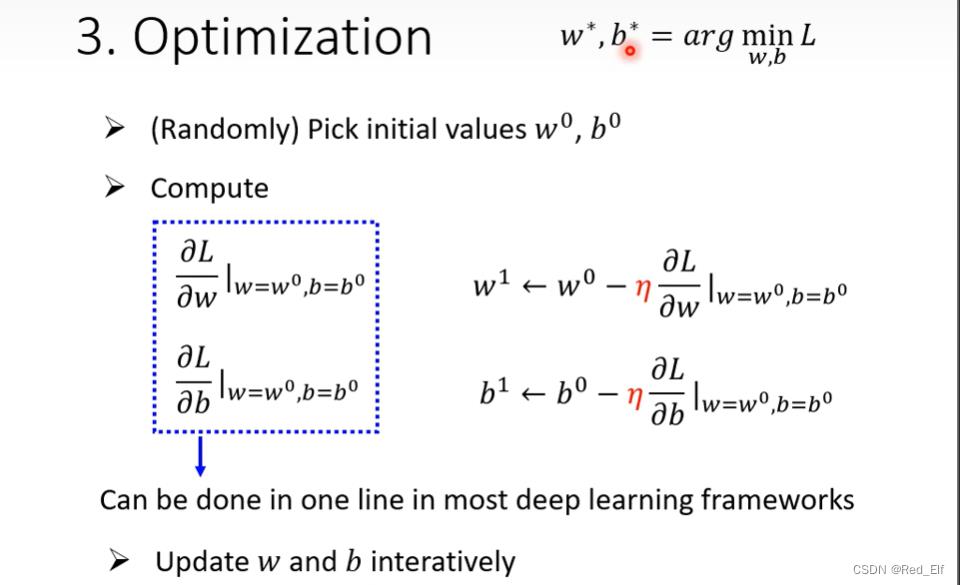
   超参数（hyper parameter）：机器学习中，需要自己设定的参数

   学习率

   全局最小值与局部最小值的问题。后续补充，在2.1部分（手动跳转吧~ 无法页面内部跳转，气死我啦ヽ(*。>Д<)o゜）

   这个问题并不是最主要的，最常见的。其实是学习率！

   找到使loss最小的$w,b$的值

   

1.3.2 改进（很牛逼，建议有基础后回看）

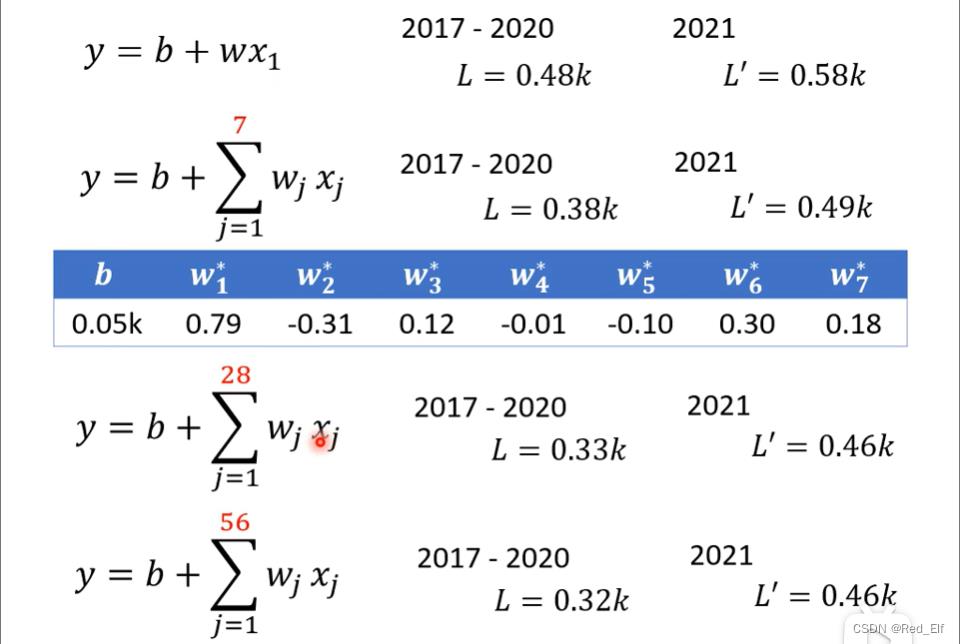
线性模型太过简单。

model bias：线性模型具有很大的限制

怎么避免model bias？需要更复杂的含有未知参数的函数。

线性函数都可以用一段一段的函数组成，即可用常数+若干个蓝色函数表示。

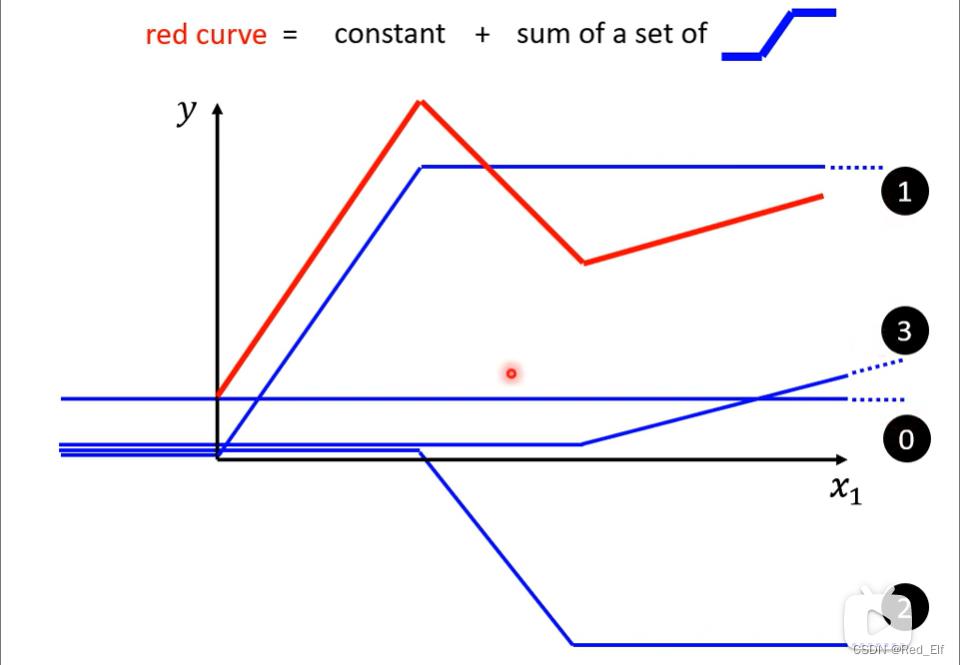
那怎么表示蓝色函数呢？

sigmoid function（S函数）：
KaTeX parse error: No such environment: align at position 8: \\begin̲a̲l̲i̲g̲n̲̲ y &= c\\frac1…

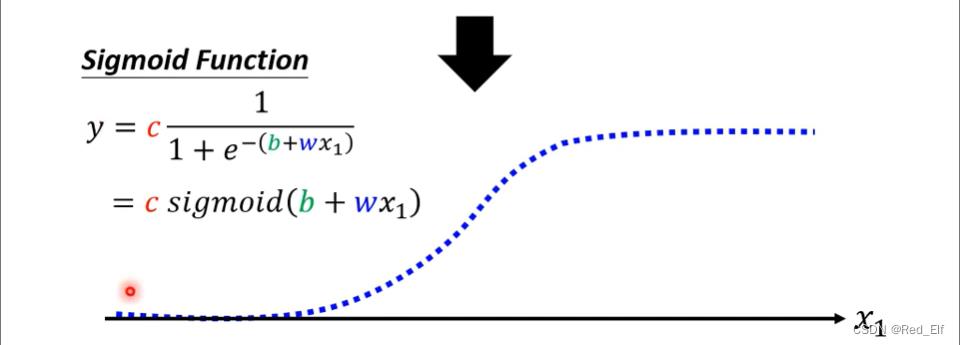
调整sigmoid函数的$c,b,w$制作各式各样的蓝色函数

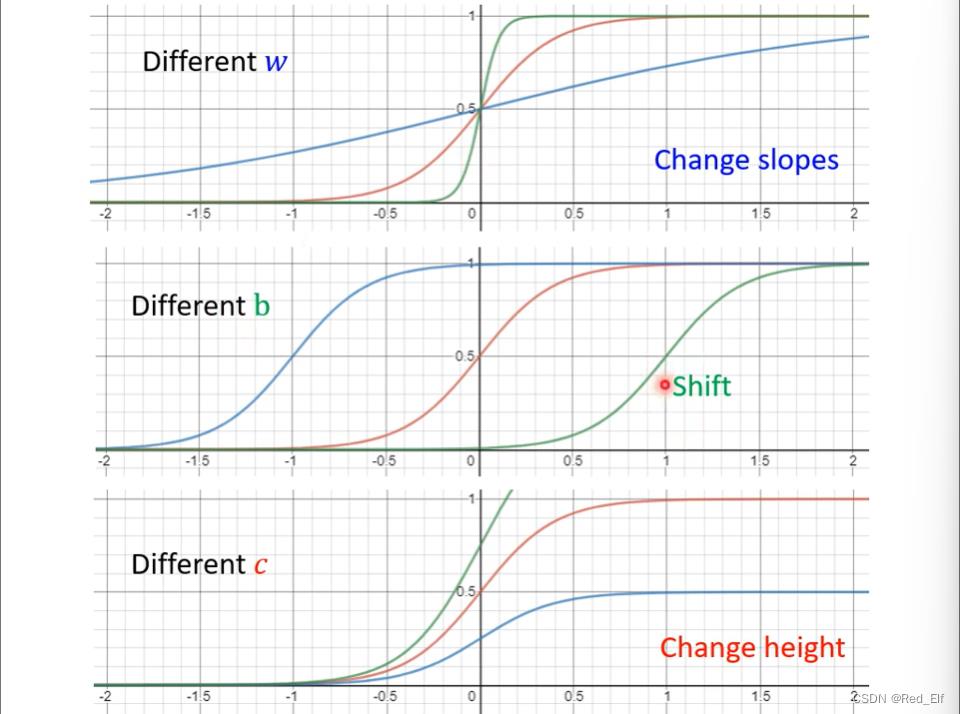
所以…
$$y=b+\sum _i{c}_{i}sigmoid(b_i+w_i{x}_1)$$

延伸一下（前方高能！！！）：

若$y=b+{\sum }_j{w}_j{x}_j$，则$y=b+{\sum }_i{c}_{i}sigmoid(b_i+{\sum }_j{w}_{ij}{x}_j)$

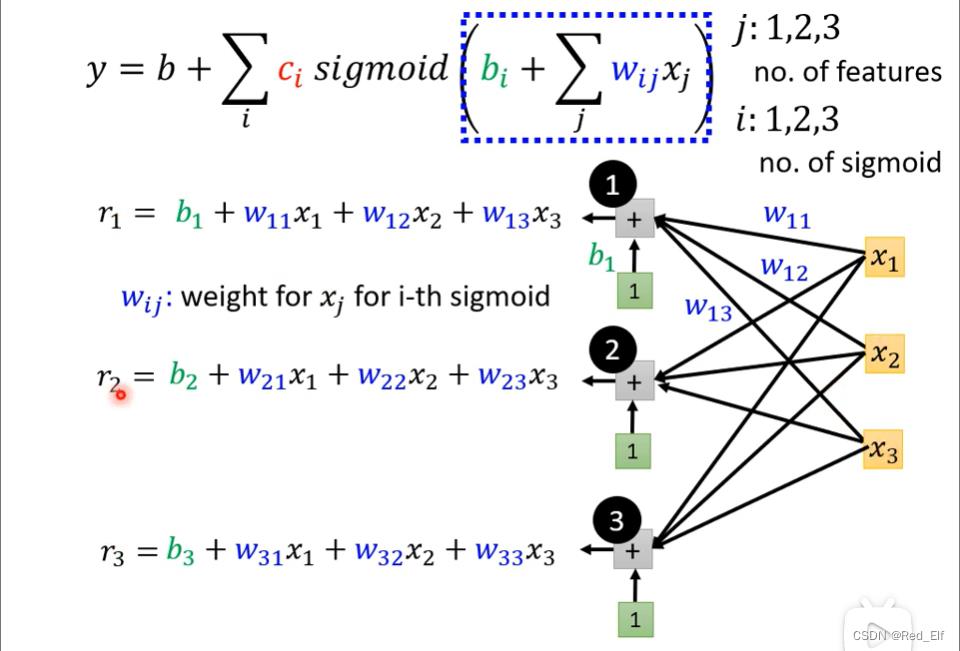
绝了哇！！！这不就是神经网络的隐藏层计算嘛！！！

用矩阵表示一下

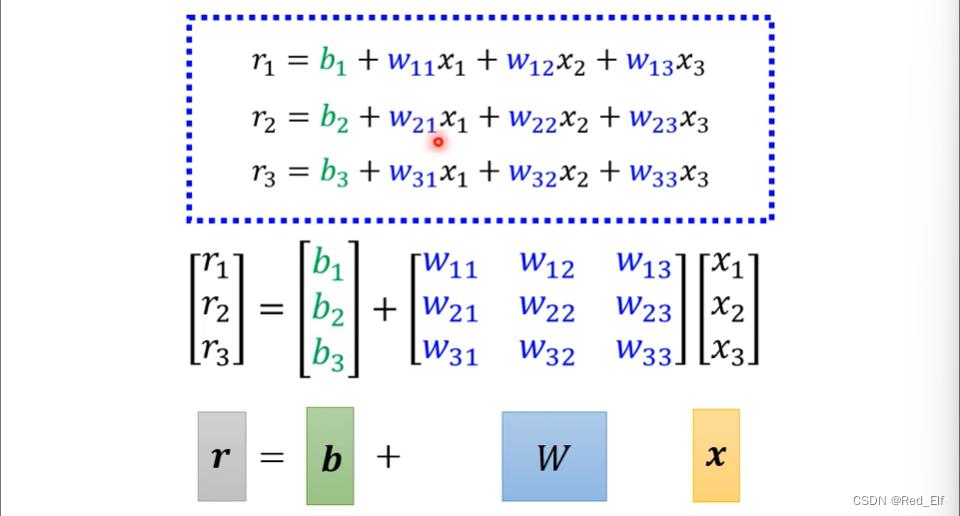
然后对每个$r$计算sigmoid
$$\alpha =\sigma (r)$$

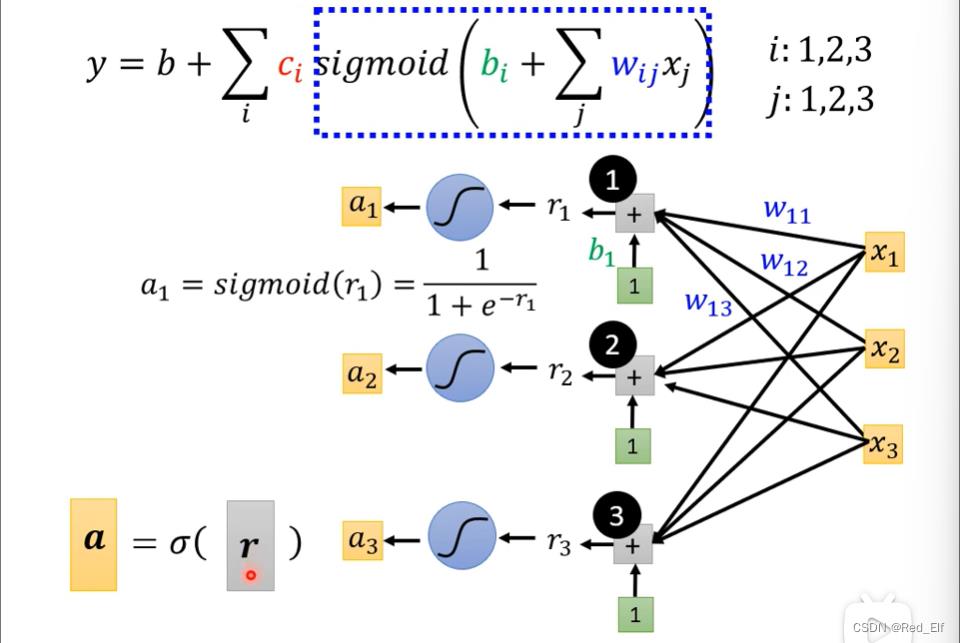
最后求y
$$y=b+c^T\alpha$$

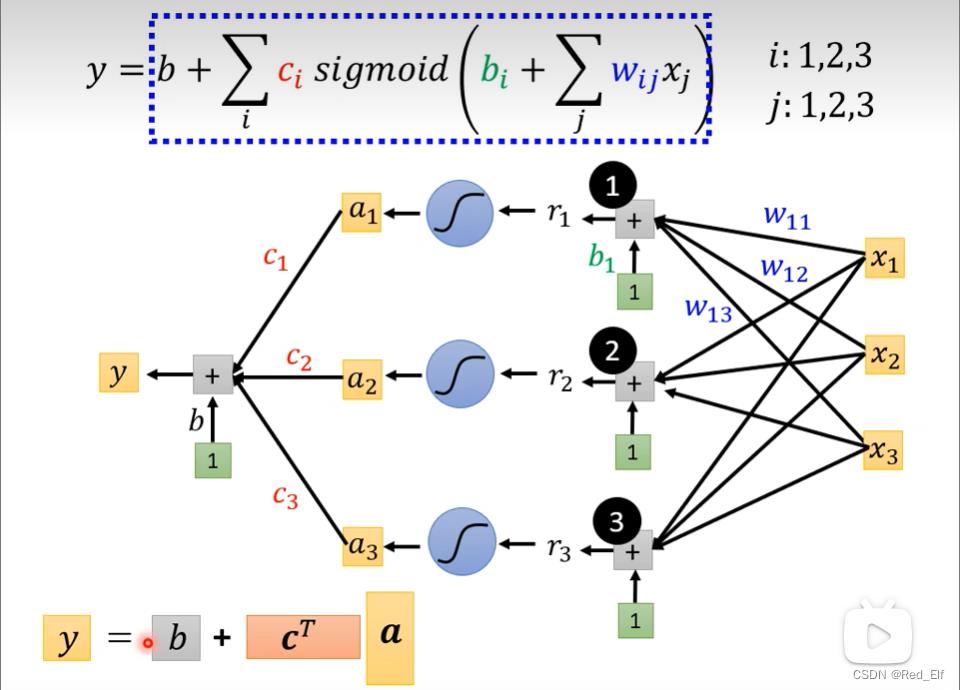
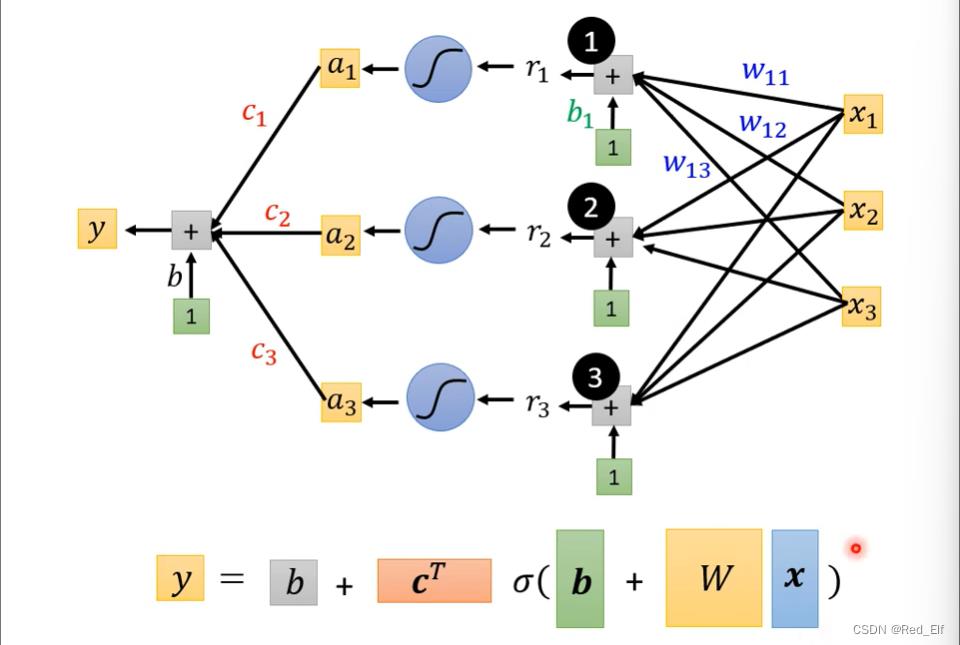
整理一下
$$y=b+c^T\sigma (b+Wx)$$

其中$x$是特征向量（feature），$W,b,c^T,b$（注意两个b不是一个意思哦~）是未知参数 ，将未知参数列成一列，统称为$\theta$.

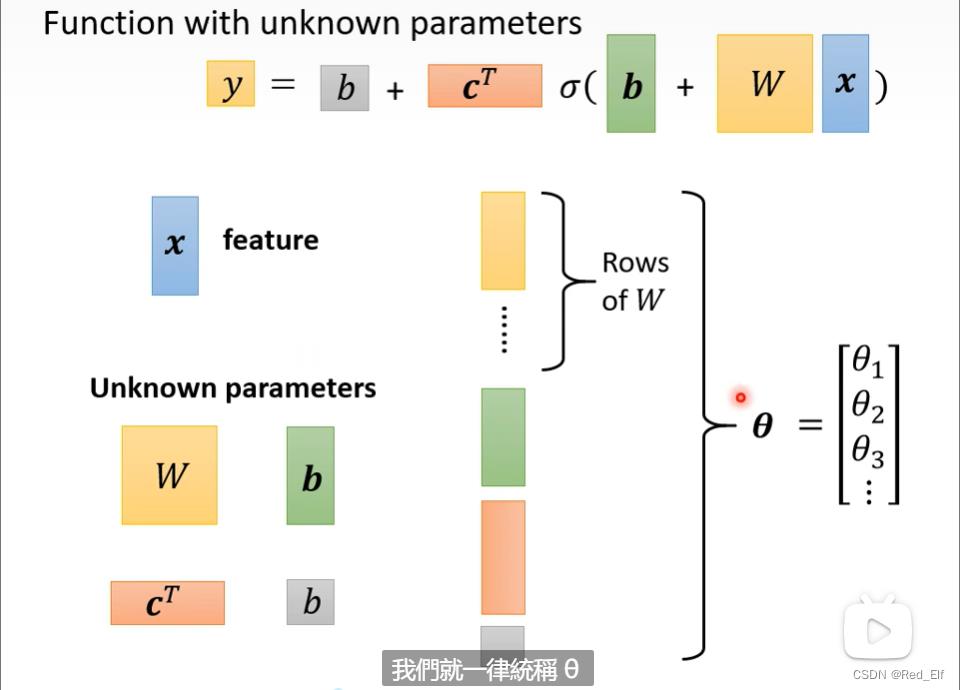
完美，更新了训练过程的第一步！！！

接下来，就是计算loss咯，没有什么变化，只是参数用$\theta$表示，因为参数太多啦。所以loss函数为$L(\theta )$.

最后是优化，

梯度 gradient。一般不会有梯度为零的情况。

可能数据很多，不方便训练，可以将数据分为几个batch（后续补充，为什么这样做，在2.2部分），用一个batch计算损失值，然后**更新（update）**参数，再选下一个batch，继续更新，直到最后一个batch。

把所有的batch看过一遍，称为一个epoch。

1.3.3 激活函数

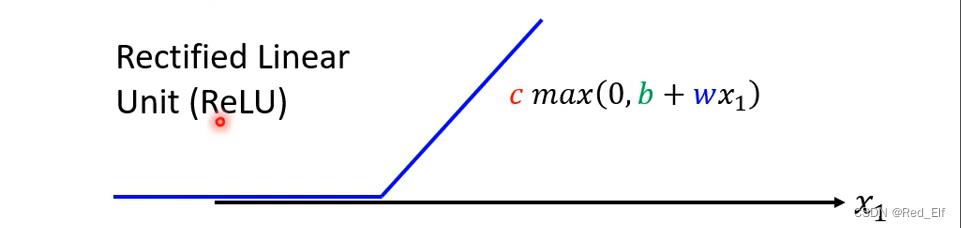
ReLU (Rectified Linear Unit)
$$y=cmax(0,b+w{x}_1)$$

Hard Sigmoid就可以用ReLU组合表示
$$y=b+\sum _{2i}{c}_{i}max(0,b_i+\sum _j{w}_{ij}{x}_j)$$
ReLU、Sigmoid就称为激活函数（activation function）

还有很多激活函数，后续补充…

对于激活函数还有一种解释：

如果都是线性关系，无论有多少层，最后都会化简成一个线性关系式，那前面的那么多层有什么用嘞，所以用激活函数将线性关系转化为非线性关系，让每一层都可以起到提取特征的作用

其实本质上都是让函数更加复杂。

1.3.4 神经网络Neural Network

可以再经历一**层（layer）**计算，层数自己设定，为超参数。

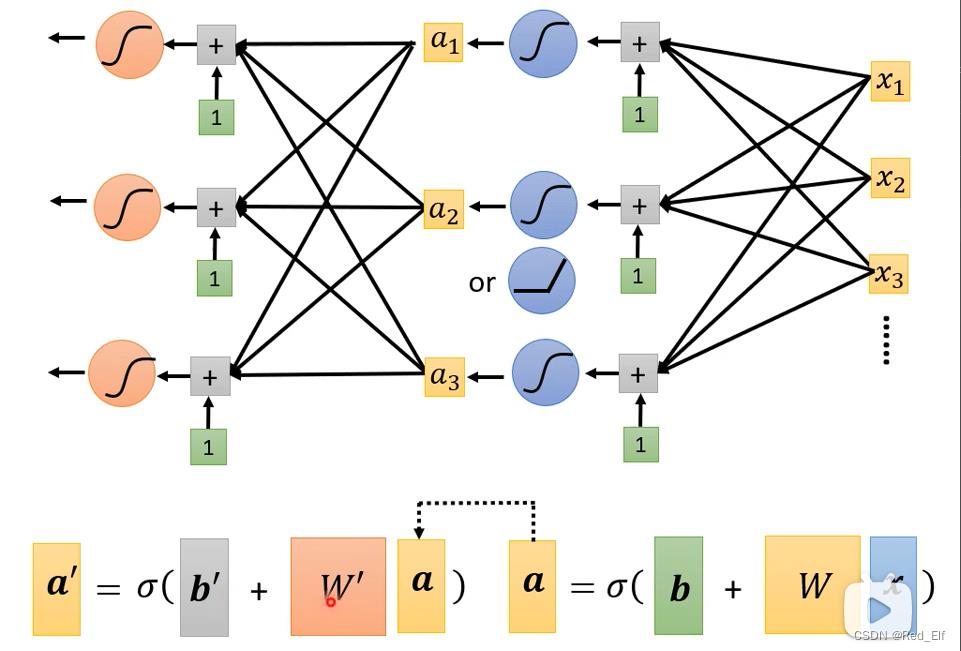
Neuron 神经元

Neural network 神经网络

换个高大上的名字

hidden layer 隐藏层

deep learning 深度学习

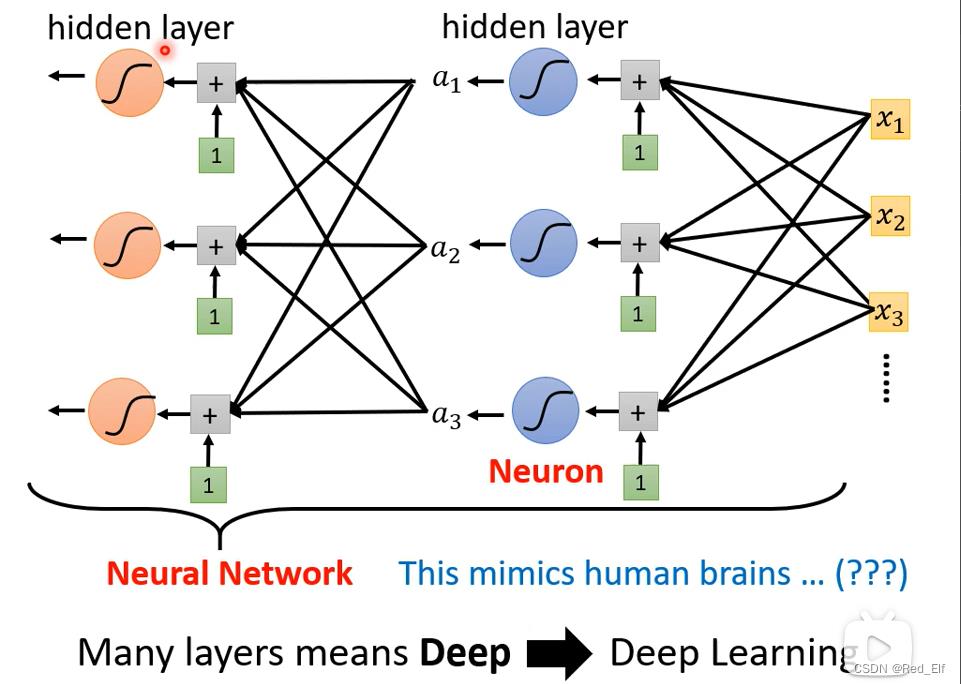
之后网络越来越深，贼多层。

但是为什么要更深，而不是更宽呢，后续补充。

越深就越好吗？不是，会出现过拟合（Overfitting），简单来说就是，练习题都会做，全对，一到考试就不会，错的离谱。

1.4 深度学习简介

• 传送门：深度学习简介

全连接前向传播神经网络 Fully connect feedforward network

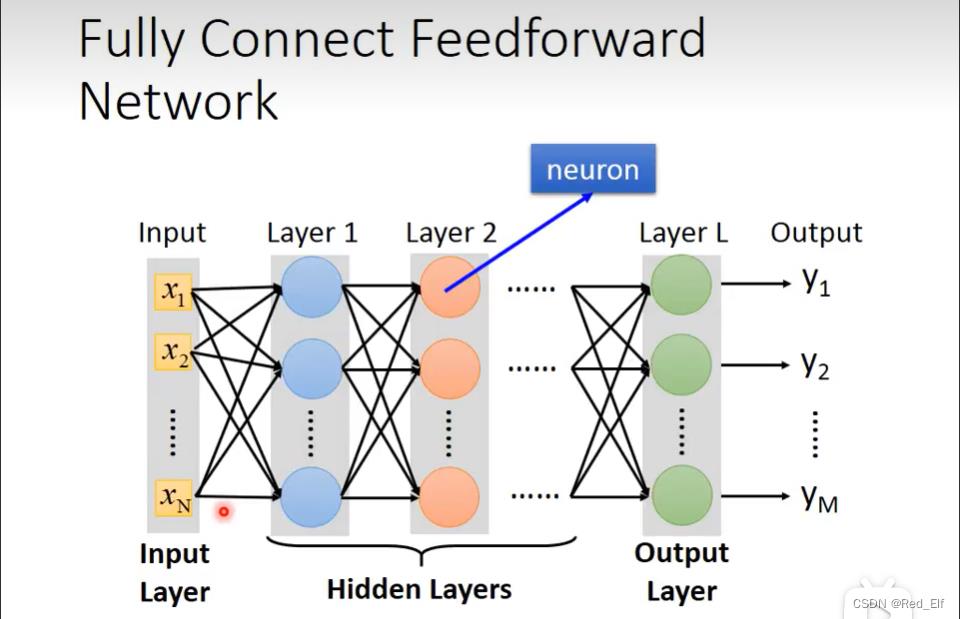
层数和神经元数的确定，嗯~，靠直觉（经验啦）。当然这个结构也是可以靠自动学习出来的（e.g. evolutionary artificial neural network）

1.4.1 反向传播（back propagation）

• 传送门：反向传播

快速计算梯度的方法而已

链式法则会吧？不会百度一下喽。

接下来是反向传播求loss值对每个参数的偏导的过程：

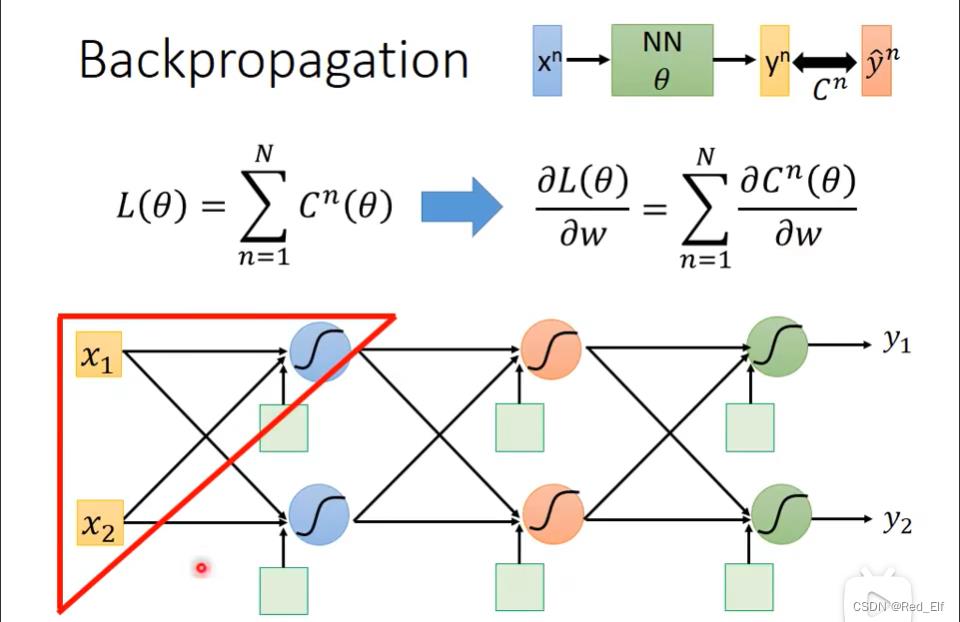
局部放大

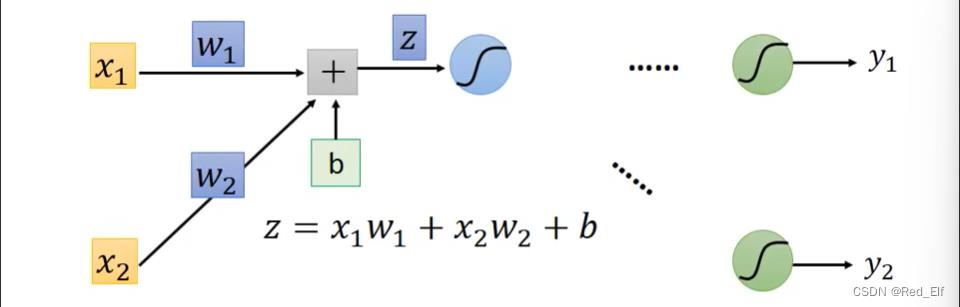
想求C对w的偏导，是不是可以用链式法则展开一下
$$\frac{\partial C}{\partial w}=$$