李宏毅机器学习课程笔记

Posted 2022-12-14 三つ叶

课程资源

B站视频
课程网址
课程笔记
问答整理

下面仅记录自己的所得所感

第一节

Regression

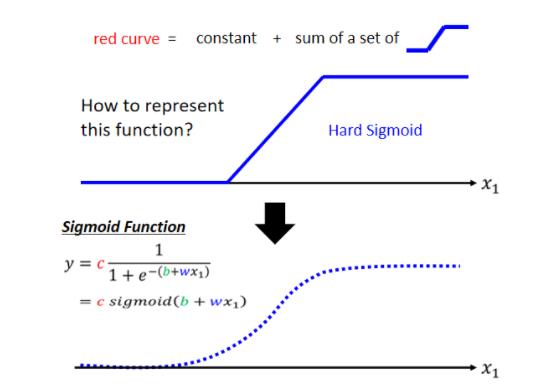
从单变量回归引入，再sigmoid/RELU拟合函数从而一步步到深度学习的框架，介绍的非常巧妙。尤其在sigmoid/RELU拟合函数那里，听了之后很有收获。
老师在引入的例子中用的x表示的是前几天的数据关系，不过我理解的时候还是觉得用特征来理解好不少。

to learn more——backpropagation

就是应用链时法则，从后往前求微分，https://blog.csdn.net/zzhhjjjj/article/details/120788339

第二节

overfitting

一般会出现这样的情况：模型太简单，出现high bias的情况（训练误差和验证误差都比较大）；模型太复杂，出现overfitting的状况（训练误差小，验证误差大）

Cross Validation

把Training的资料分成两半,一部分叫作Training Set,一部分是Validation Set
你在Validation Set上面,去衡量它们的分数,你根据Validation Set上面的分数,去挑选结果，最终在test set中去测评模型的泛化能力。

N-fold Cross Validation

N-fold Cross Validation就是你先把你的训练集切成N等份,在这个例子裡面我们切成三等份,切完以后,你拿其中一份当作Validation Set,另外两份当Training Set,然后这件事情你要重复三次

也就是说,你先第一份第二份当Train,第三份当Validation,然后第一份第三份当Train,第二份当Validation,第一份当Validation,第二份第三份当Train

然后接下来 你有三个模型,你不知道哪一个是好的,你就把这三个模型,在这三个setting下,在这三个Training跟Validation的,data set上面,通通跑过一次,然后把这三个模型,在这三种状况的结果都平均起来,把每一个模型在这三种状况的结果,都平均起来,再看看谁的结果最好

Local Minimum And Saddle Point

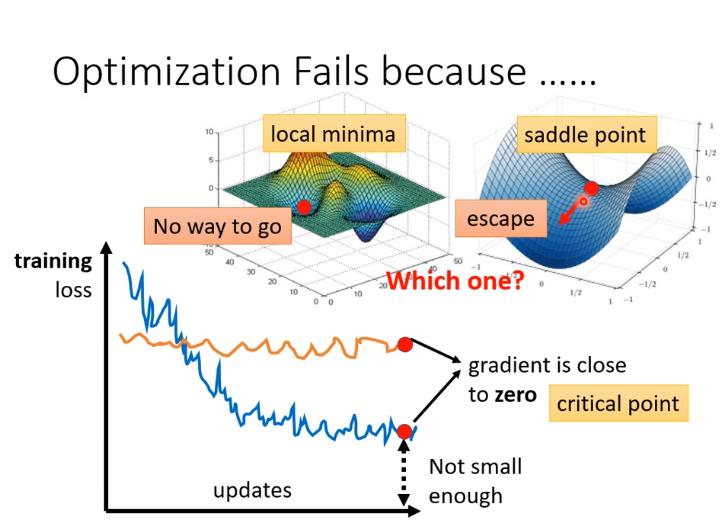
过去常见的一个猜想,是因為我们现在走到了一个地方,这个地方参数对loss的微分為零

讲到gradient為零的时候,大家通常脑海中最先浮现的,可能就是local minima。

但gradient为零还可能是其他情况,比如说 saddle point,所谓的saddle point,像图中显示那样,它在左右这个方向是比较高的,前后这个方向是比较低的,它就像是一个马鞍的形状,所以叫做saddle point,那中文就翻成鞍点

像saddle point这种地方,它也是gradient為零,但它不是local minima,那像这种gradient為零的点,统称為critical point,所以你可以说你的loss,没有办法再下降,也许是因為卡在了critical point,但你不能说是卡在local minima,因為saddle point也是微分為零的点

判断微分为0的情况

要知道我们loss function的形状,可是我们怎麼知道,loss function的形状呢,network本身很复杂,用复杂network算出来的loss function,显然也很复杂,我们怎麼知道loss function,长什麼样子,虽然我们没有办法完整知道,整个loss function的样子

但是如果给定某一组参数,比如说蓝色的这个${\theta }^{{}^{\prime }}$,在${\theta }^{{}^{\prime }}$附近的loss function,是有办法被写出来的,它写出来就像是这个样子

那如果我们今天走到了一个critical point,意味著gradient為零,也就是绿色的这一项完全都不见了

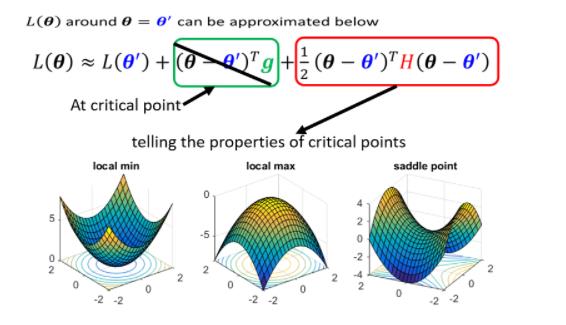
判断方法如下

Don’t afraid of saddle point

对于saddle point的情况，从图中我们也可以形象地看出它的loss是有办法可以继续下降的

Saddle Point v.s. Local Minima

当维度很多的时候，其实我们是有很多“路”可以走的，很难出现真正H为正定的情况

从经验上看起来,其实local minima并没有那麼常见,多数的时候,你觉得你train到一个地方,你gradient真的很小,然后所以你的参数不再update了,往往是因為你卡在了一个saddle point

Batch and Momentum

Batch

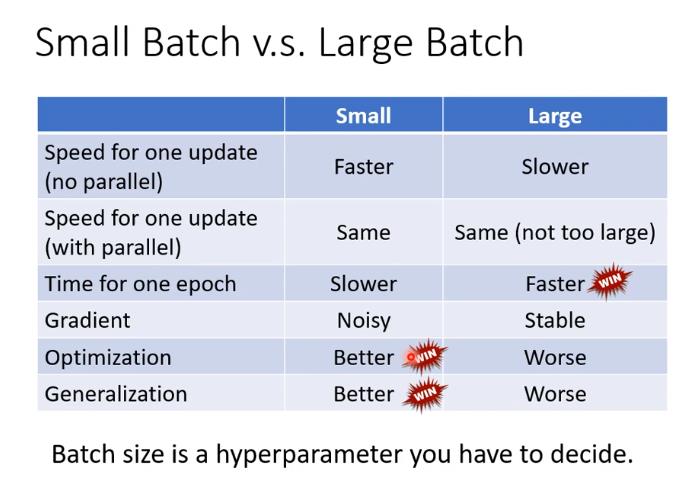
介绍了small batch和large batch的优缺点，并且解释了产生这些现象的原因，建议直接看原文

Momentum

加上 Momentum 以后,每一次我们在移动我们的参数的时候,我们不是只往 Gradient Descent,我们不是只往 Gradient 的反方向来移动参数,我们是** Gradient 的反方向,加上前一步移动的方向**,两者加起来的结果,去调整去到我们的参数,

Conclude：Smaller batch size and momentum help escape critical points.

Adaptive Learning Rate

如果在某一个方向上,我们的gradient的值很小,非常的平坦,那我们会希望learning rate调大一点,如果在某一个方向上非常的陡峭,坡度很大,那我们其实期待,learning rate可以设得小一点。因此，我们希望learning rate可以自适应的进行调整。

RMSProp

在RMS Prop裡面,它决定你可以自己调整,现在的这个gradient,你觉得它有多重要

Adam

Learning Rate Scheduling

让$\eta$成为一个随时间改变调整的量

(一)、什么是Warmup?
Warmup是在ResNet论文中提到的一种学习率预热的方法，它在训练开始的时候先选择使用一个较小的学习率，训练了一些epoches或者steps(比如4个epoches,10000steps),再修改为预先设置的学习率来进行训练。

(二)、为什么使用Warmup?
由于刚开始训练时,模型的权重(weights)是随机初始化的，此时若选择一个较大的学习率,可能带来模型的不稳定(振荡)，选择Warmup预热学习率的方式，可以使得开始训练的几个epoches或者一些steps内学习率较小,在预热的小学习率下，模型可以慢慢趋于稳定,等模型相对稳定后再选择预先设置的学习率进行训练,使得模型收敛速度变得更快，模型效果更佳。

ExampleExampleExample：Resnet论文中使用一个110层的ResNet在cifar10上训练时，先用0.01的学习率训练直到训练误差低于80%(大概训练了400个steps)，然后使用0.1的学习率进行训练。

(三)、Warmup的改进
(二)所述的Warmup是constant warmup，它的不足之处在于从一个很小的学习率一下变为比较大的学习率可能会导致训练误差突然增大。于是18年Facebook提出了gradual warmup来解决这个问题，即从最初的小学习率开始，每个step增大一点点，直到达到最初设置的比较大的学习率时，采用最初设置的学习率进行训练。

Summary of Optimization

那讲到这边可能有同学会觉得很困惑,这一个momentum是考虑,过去所有的gradient,这个σ也是考虑过去所有的gradient,一个放在分子一个放在分母,都考虑过去所有的gradient,不就是正好抵销了吗,

但是其实这个Momentum跟这个σ,它们在使用过去所有gradient的方式是不一样的,Momentum是直接把所有的gradient通通都加起来,所以它有考虑方向,它有考虑gradient的正负号,它有考虑gradient是往左走还是往右走

但是这个Root Mean Square,它就不考虑gradient的方向了,它只考虑gradient的大小,记不记得我们在算σ的时候,我们都要取平方项,我们都要把gradient取一个平方项,我们是把平方的结果加起来,所以我们只考虑gradient的大小,不考虑它的方向,所以Momentum跟这个σ,算出来的结果并不会互相抵销掉

Batch Normalization

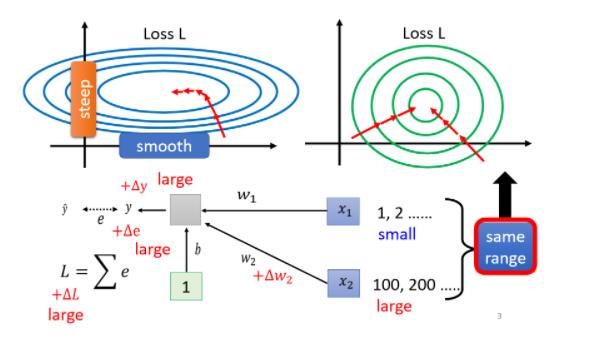
为什么要Normalization？
如上图所示，当我们 input 的 feature,每一个 dimension 的值,它的 scale 差距很大的时候,我们就可能產生像这样子的 error surface（左图）,就可能產生不同方向,斜率非常不同,坡度非常不同的 error surface。
如果我们可以给不同的 dimension,同样的数值范围的话,那我们可能就可以製造比较好的 error surface,让 training 变得比较容易一点，即如右图所示。

在具体的Feature Normalization中，还会有各种各样的问题和解决手段，如何Normalization？deeping learning的每一个layer是否都需要Normalization？如何对testing数据集Normalization？

To learn more——Optimization for Deep Learning

由于这两集没有找到相关的课程笔记，我将在这篇文章中加以记录学习

第三节

Classification

label的表示

分类问题有别于回归问题，在分类问题中，我们一般采用One-hot vector的方法表示分类结果(label的表示)。所谓One-hot vector，就是将所有分类结果排成一个列向量，每个元素为一个分类结果，元素为1，则代表其对应的分类结果为该One-hot vector的结果

Classification with softmax

经过刚刚的讨论，我们知道了label的表示，那么我们在训练时，是怎么将features一步步得到最终的预测结果的呢？过程又与Regression又有什么不同呢？

通过上图，我们可以看到，Classification的训练过程相比于Regression问题，其实就是在Regression的结果后再加一个softmax函数，那么softmax其实就是下面这个样子
$$y_i^{{}^{\prime }}=\frac{exp(y_i)}{{\sum }_{j}exp(y_i)}$$
图示化如下

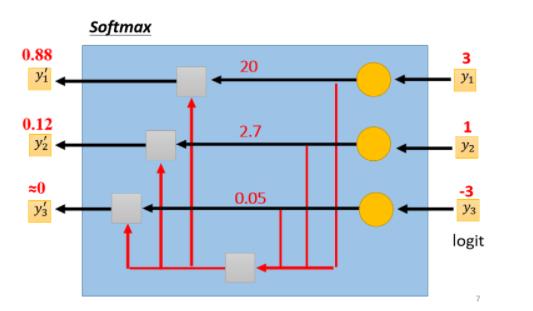
具体为什么要用softmax，参阅

Loss of Classification

就我之前所了解的，Classification的问题的损失函数为
$$-\ln (w,b)=\sum _i^n-[{\hat{y}}^i\ln f_{w,b}(x^i)+(1-{\hat{y}}^i)\ln (1-f_{w,b}(x^i))]$$

但是，当我试图将多分类的问题套用在这个公式的时候，才发现？？？压根套不上呀！

事实上，上式仅仅是对多分类损失函数在二分类问题上的一个形式。真正的形式理应是这样的
$$-\ln L(w,b)=\sum _i^n\sum _k^m-{\hat{y}}_k^i\ln f_{w,b}(x_k^i)$$

举个栗子，假设我们的一个sample经过softmax后得到的$y=f_{w,b}(x)=\left[\begin{array}{c}0.9\\ 0.1\end{array}\right]$，其label为$\hat{y}=\left[\begin{array}{c}1\\ 0\end{array}\right]$，那么在第一个式子里计算出的值为 $-(1\ln 0.9+0\ln 0.1)=-\ln 0.9$，第二计算结果即为$-\ln 0.9-0\ln 0.1$。再比方说，我们的另一个sample经过softmax后得到的$y=f_{w,b}(x)=\left[\begin{array}{c}0.1\\ 0.8\\ 0.1\end{array}\right]$,其label为$\hat{y}=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$,此时我们有$-\ln L(w,b)=-0\ln 0.1-1\ln 0.8以上是关于李宏毅机器学习课程笔记的主要内容，如果未能解决你的问题，请参考以下文章$

李宏毅机器学习课程笔记

学习笔记李宏毅2021春机器学习课程第5.1节：Transformer

李宏毅2020机器学习深度学习笔记1+2 &&深度学习基础与实践课程笔记2

李宏毅机器学习笔记（2016年的课程）：Support Vector Machine (SVM)

李宏毅机器学习笔记（2016年的课程）：Support Vector Machine (SVM)

学习笔记李宏毅2021春机器学习课程第7.2节：自监督学习