正则化小结
Posted 栋次大次
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了正则化小结相关的知识,希望对你有一定的参考价值。
正则化
L1
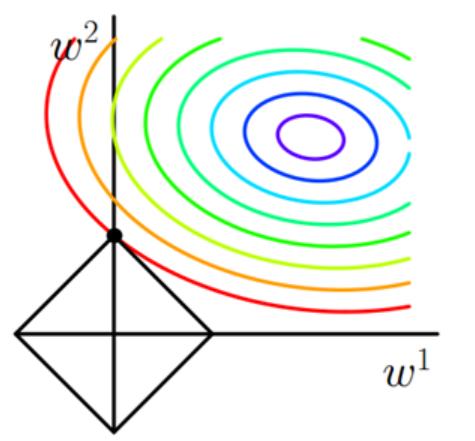
L1正则项就是一个L1范数,相当于为模型添加了一个先验知识:w服从零均值拉普拉斯分布。
J = J 0 + α ∑ w ∣ w ∣ J=J_0+\\alpha \\sum_w|w| J=J0+α∑w∣w∣
增加了对所有权重w参数的绝对值之和,迫使更多的w为零,使得产生稀疏模型。
L2
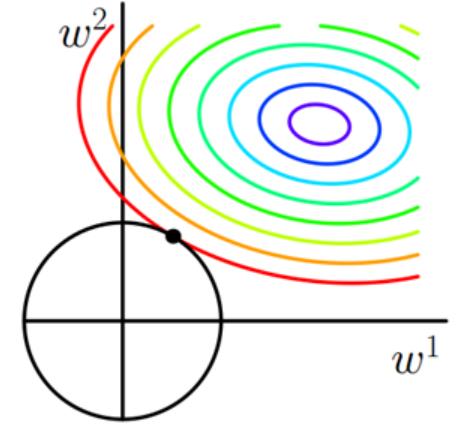
J = J 0 + α ∑ w w 2 J=J_0+\\alpha \\sum_w w^2 J=J0+α∑ww2
增加所有权重w参数的平方之和,迫使w尽可能趋向于零但不为零(L2的导师趋于零)。
L2正则化和过拟合的关系:
拟合过程通常都倾向于让权值尽可能的小,最后构造一个所有参数都比较小的模型。一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。(若参数很大,那么只要数据偏移一点,就会对结果造成很大的影响,如果参数小,抗扰动能力强)
不用L0正则化的原因:
根据上边的讨论,系数参数可以防止过拟合,因此用L0范数(非零参数的个数)正则项可以防止过拟合。
但具体中,L0正则项很难求解,是个NP难问题。
不正则化参数b的原因:
如果对b进行惩罚,其实作用不大,因为在输出结果的贡献中,参数b对于输入的改变时不敏感的,参数b只是加了偏置。w会对不同的数据产生不一样的加权。
稀疏:对于模型,指的是参数有较少的非零值,其作用有:
- 去掉冗余特征,使模型更简单,防止过拟合
- 降低运算量,防止维度爆炸。
batchnorm
随着深度神经网络多层的叠加,每一层的参数更新会导致上层的输入数据分布发生变化,层层叠加导致高层的输入分布变化会非常剧烈,使得高层需要不断去重新适应底层的参数更新。
随着网络加深,参数分布不断往激活函数两端移动(梯度变小),导致反向传播出现梯度消失,收敛困难。
原理:在每层激活函数前,加入BN,将参数重新拉回0-1正太分布,加速收敛。
理想情况下,normalization的均值和方差应当是整个数据集,但为了简化计算,就采用mini_batch的操作。机器学习中的白话(eg. PCA)也可以起到规范化分布的作用,但是计算成本过高。

BN最后一步是缩放操作,加入两个学习参数,用于保持模型的表达能力。(不加缩放,每层学习的特征都被归一化为标准的正太分布,降低模型的表达能力)。
训练和测试:测试时均值和方差不再用每个mini-batch来代替,而是训练过程中记录下每个batch的均值和方差,训练完成后计算整体均值和方差用于测试。可学习参数固定。
四种主流的normalization:
- batch normalization:纵向规范化
- layer normalization:对于单个样本
- weight normalization:对于参数
- cosine normalization:余弦规范化,同时考虑参数和数据
BN对于Relu是否有效?
有效。学习率稍微设置大一点,Relu函数就会落入负区间,神经元无法激活,导致dead relu问题。BN可以将数据分布拉回来。
多卡同步
原因:对于BN来说,用batch的均值和方差来估计全局的均值和方差,但因此batch越大越好,但一张卡容量有效,过小batch起不到bn的归一化效果。
原理:利用多卡同步,单卡计算后,多卡之间通信计算出整体的均值和方差,用于bn计算,等同于batchsize大小。
2次同步?第一次同步获得全局均值,然后第二次计算全局方差。
1次同步?一次传递完成,计算出全局均值和方差。
总结:
- 加入Bn可以放心调参,较大的学习率可以提高学习速度
- Bn降低了数据之间的绝对差异,有一个去相关的性质,更多的考虑从相对差异性,因此在分类任务上有更好的效果。
layernorm
LN通常用在RNN网络,RNN可以展开成一个隐藏层共享参数的MLP,随着时间片的增多,展开后的MLP的层数也在增多,最终层数由输入数据的时间片数量决定。
在一个batch中,各个样本长度不同(针对时序数据:语音等),在后边的时间片,只有一个样本还有数据,基于这个样本的统计信息不能反映全局分布,所以这时BN的效果不好。
设
H
H
H 是一层中隐层节点的数量,
l
l
l 是层数,我们可以计算LN的归一化统计量
μ
\\mu
μ 和
σ
\\sigma
σ :
μ
l
=
1
H
∑
i
=
1
H
a
i
l
σ
l
=
1
H
∑
i
=
1
H
(
a
i
l
−
μ
l
)
2
\\mu^l=\\frac1H \\sum_i=1^H a_i^l \\quad \\sigma^l=\\sqrt\\frac1H \\sum_i=1^H\\left(a_i^l-\\mu^l\\right)^2
μl=H1i=1∑Hailσl=H1i=1∑H(ail−μl)2
注意上面统计量的计算是和样本数量没有关系的,它的数量只取决于隐层节点的数量,所以只要隐层节点的数量足够多,我们就能保证
L
N
L N
LN 的归一化统计量足够具有代表性。通过
μ
l
\\mu^l
μl 和
σ
l
\\sigma^l
σl 可以得 到归一化后的值
a
^
l
\\hata^l
a^l :
a
^
l
=
a
l
−
μ
l
(
σ
l
)
2
+
ϵ
\\hat\\mathbfa^l=\\frac\\mathbfa^l-\\mu^l\\sqrt\\left(\\sigma^l\\right)^2+\\epsilon
a^l=(σl)2+ϵal−μl
其中
ϵ
\\epsilon
ϵ 是一个很小的小数,防止除 0 (论文中忽略了这个参数)。
在LN中我们也需要一组参数来保证归一化操作不会破坏之前的信息,在LN中这组参数叫做增益 (gain)
g
g
g 和偏置 (bias)
b
b
b (等同于BN中的
γ
\\gamma
γ 和
β
\\beta
β ) 。假设激活函数为
f
f
f ,最终LN的输 出为:
h
l
=
f
(
g
l
⊙
a
^
l
+
b
l
)
\\mathbfh^l=f\\left(\\mathbfg^l \\odot \\hat\\mathbfa^l+\\mathbfb^l\\right)
hl=f(gl⊙a^l+bl)
https://zhuanlan.zhihu.com/p/54530247
https://www.jianshu.com/p/91b54246b51c
dropout
减轻过拟合。(相当于间接的多模型 )
原理:前向传播时按照概率p随机关闭神经元。在本次反向传播时,只更新未关闭的神经元。下次训练时恢复,重复两个操作。
训练和测试
测试时需要关闭dropout,否则仍然随机关闭神经元,导致网络不稳定。
若什么都不做,会导致训练和测试结果不同。为了平衡训练和测试的差异,采取使训练和测试的输出期望相等的操作。
训练时除以p:假设一个神经元的输出激活值为a,在不使用dropout的情况下,其输出期望为a,如果使用dropout,神经元就可能有保留和关闭两种状态,把它看作一个离散型随机变量,它就符合概率论的0-1分布,其输出激活值的期望变为p*a+(1-p)*0=pa,此时若保持期望和不使用dropout时一致,需要除以p,反之测试需要乘p。
为什么可以降低过拟合?
- ensemble效果:训练过程中每次随机关闭不同的神经元,网络结构已经发生变化,整个dropout的训练过程相当于很多不同的网络取平均,进而达到ensemble效果。
- 减少神经元之间复杂的共适应性关系:dropout导致每两个神经元不一定每一次都出现在网络中,减轻神经元之间的依赖关系,迫使网络无法关注特殊情况,而只能学习一些更加鲁棒的特征。
BN和dropout共同使用出现的问题:
dropout为了平衡训练和测试之间的差异,会通过随机失活对的概率来对神经元进行缩放,进而会改变方差。如果再加一层BN,又会将方差拉回(0,1)分布,进而产生冲突。
处理方法:
- 始终将dropout放在BN后
- 使用高斯Dropout
过拟合 欠拟合 防止的方法
欠拟合:模型复杂度低,在训练集上表现就很差,一般刚开始训练是欠拟合。
措施:增加网络的复杂度或者在模型中增加特征
过拟合:训练误差和测试误差之间差距太大。模型过于复杂,过度拟合训练集,泛化能力差。
原因:1. 训练数据样本单一,样本不足。2. 训练数据中噪声干扰过大。噪声指训练数据中的干扰数据,过多的干扰会导致记录了很多噪声特征,忽略了真实输入和输出之间的关系。3. 模型过于复杂。
措施:
-
数据增强(结果过拟合的根本性方法)
-
控制模型的复杂度,选择合适的模型
-
降低特征的数量,删除冗余特征。
-
L1和L2正则化
-
dropout
-
提前终止训练。为什么能防止?开始迭代,w的值会变得越来越大,到后边会很大,所以提前终止,就是在中间点停止迭代,将会得到一个合适的值,于L2的效果相似。
缺点:没有采取不同的方式来解决优化损失函数和过拟合这两个问题。考虑的东西变得复杂,停止了优化,可能会发现算是函数的值不够小,同时又不希望过拟合。
https://zhuanlan.zhihu.com/p/356298455
各位读者老爷,求个赞,点个关注😜
欢迎交流深度学习,语音识别,声纹识别等相关知识
以上是关于正则化小结的主要内容,如果未能解决你的问题,请参考以下文章