利用凸变形解决”安装栅栏“问题

Posted 2022-11-25 &小小白&

二十一、安装栅栏

21.1、题设要求

  在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。

示例 1:

输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]

解释:

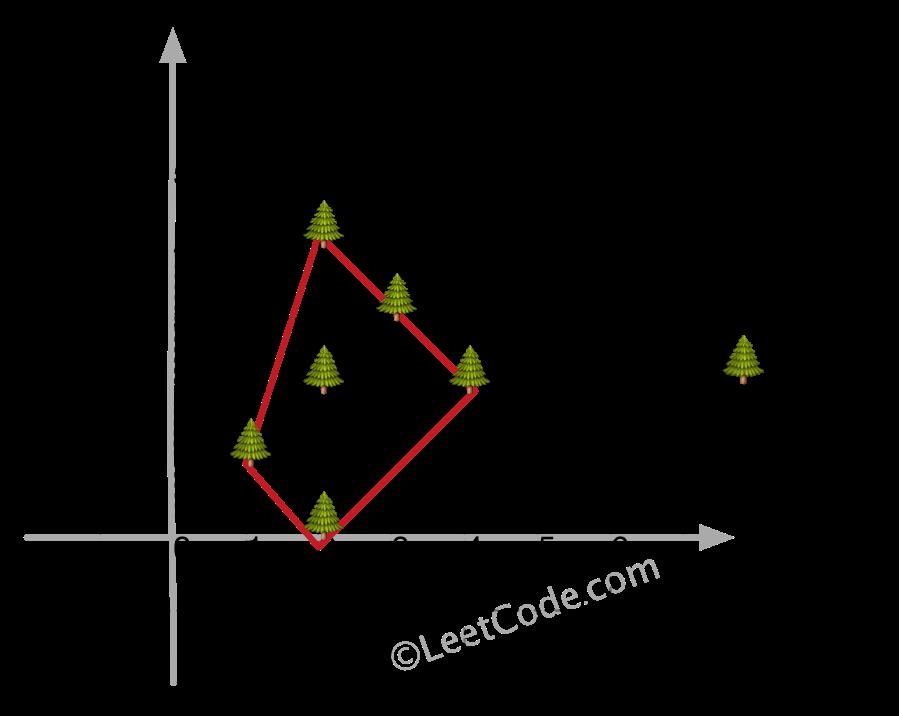
示例 2:

输入: [[1,2],[2,2],[4,2]]
输出: [[1,2],[2,2],[4,2]]

解释:

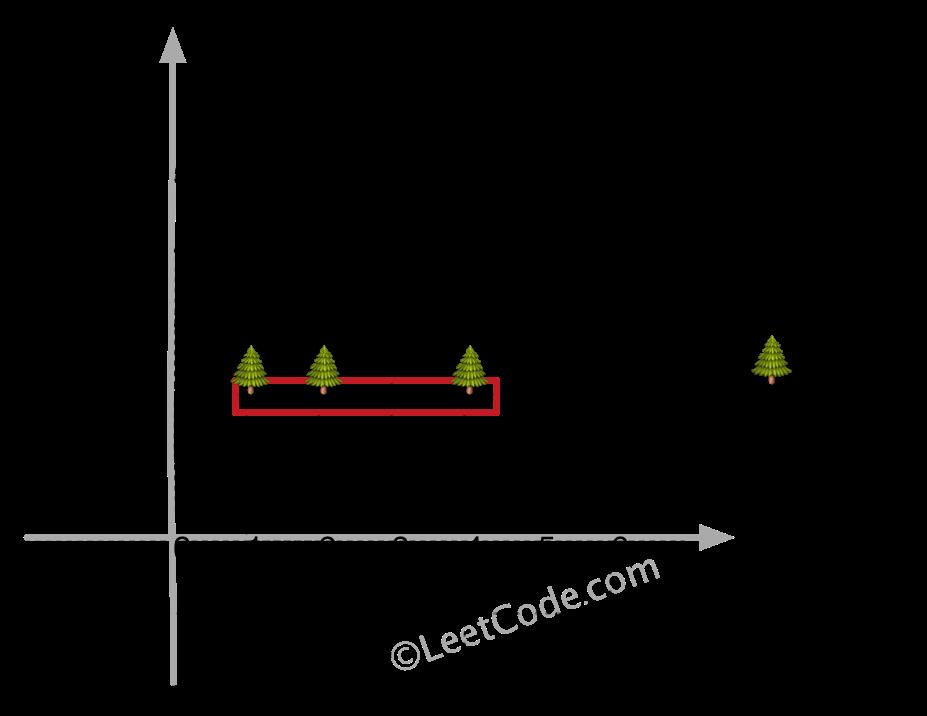
  即使树都在一条直线上，你也需要先用绳子包围它们。

注意:

所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
输入的整数在 0 到 100 之间。
花园至少有一棵树。
所有树的坐标都是不同的。
输入的点没有顺序。输出顺序也没有要求。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/erect-the-fence

21.2、解题思路

  向量叉积：向量pq和向量qr的叉积可以判别，r相对于pq的方向，大于0在向量pq的左侧，小于0，在向量pq的右侧

方法：Andrew

1. 排序，x从小到大排序，x相等的情况，按y从小到大排序
2. 最左边的点一定属于外边界（不然其他点围不住它）
3. 左到右：按照数组顺序逐渐添加新的点，选择的倒数第二个点为p,倒数第一个点为q,现在的点为r
   3.1、假设使用向量叉积可以判别r在pq右侧，则可放弃q,使用使用pr

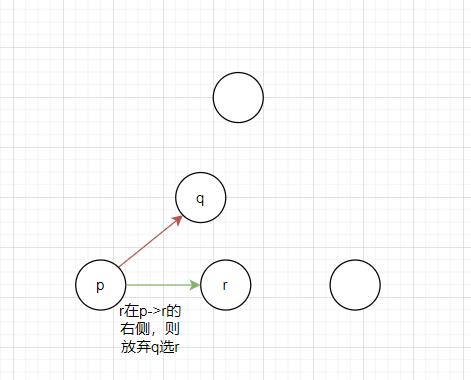
    这个过程删除q点
    r在pq左侧或同向的情况，添加r
  4. 右到左：按照数组顺序逐渐添加新的点，选择的倒数第二个点为p,倒数第一个点为q,现在的点为r
  和 3 的过程相同，都是不断判别r是否在pq右侧，从而选择是否放弃q的过程
  区别：
    需要判别是否已访问，已访问点不要重复访问

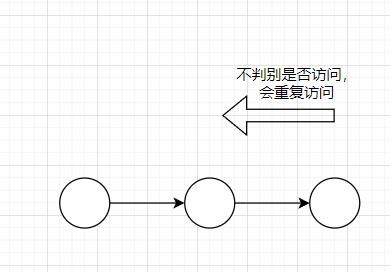
  遍历过程必须加入最左侧点，因为需要删除右到左的凹下去的形状，回到最左侧可以删掉部分多余的点

  最终结果需要排除掉最左侧点，因为头尾写了两次

  先找到所有树中最左边的树,然后找到最左边的树的下一颗树并添加到list中,然后将list转换成arr即可。

21.3、算法

class Solution 
    public int[][] outerTrees(int[][] trees) 
        int n = trees.length;
        //如果树的个数小于4并且在一条直线上,直接输出即可
        if (n < 4 || onSameLine(trees))
            return trees;
        
        int l = 0;
        //找到最左边的点
        for (int i = 0; i < n; i++) 
            if (trees[l][0] > trees[i][0])
                l = i;
            
        
        int p = l;
        List<int[]> list = new ArrayList<>();
        //找到下一个点并添加到数据结构中
        do 
            list.add(trees[p]);
            int q = (p + 1) % n;
            //得到下一个点
            for (int i = 0; i < n; i++) 
                if (i != p && i != q && orientation(trees[p], trees[q], trees[i]) == 1)
                    q = i;
                
            
            //是否在一条直线上
            for (int i = 0; i < n; i++) 
                if (i != p && i != q && onSegement(trees[p], trees[q], trees[i]))
                    list.add(trees[i]);
                
            
            p = q;
        while (p != l);
        int[][] res = new int[list.size()][2];
        //将list中的数据赋值给res并返回结果
        for (int i = 0; i < list.size(); i++) 
            res[i][0] = list.get(i)[0];
            res[i][1] = list.get(i)[1];
        
        return res;
    

    //判断是顺时针方向还是逆时针方向
    /**
    当val为1时,逆时针方向;
    当val为2时,顺时针方向;
    当val为0时,水平方向.
     */
    private int orientation(int [] p,int [] q,int[] r)
        int val = (q[1] - r[1]) * (r[0] - p[0]) - (q[0] - r[0]) * (r[1] - p[1]);
        if (val == 0)
            return 0;
        
        return val > 0 ? 1 : 2;
    

    //返回符合条件的点
    private boolean onSegement(int[] p,int[] q,int[] r)
        return r[0] >= Math.min(p[0], q[0]) && r[0] <= Math.max(p[0], q[0])
                && r[1] >= Math.min(p[1], q[1]) && r[1] <= Math.max(p[1], q[1])
                && orientation(p, q, r) == 0;
    

    //判断是否在一条线上
    private boolean onSameLine(int[][] points)
        for (int i = 0; i < points.length - 2; i++) 
            if (orientation(points[i], points[i + 1], points[i + 2]) != 0)
                return false;
            
        
        return true;
    

参考视频：B站up主郭郭 wg
参考文章：力扣up主钰娘娘