混沌动力学行为研究-分叉图

Posted 2022-03-14 studyer_domi

混沌动力学行为研究的程序说明

1.分岔图：

一个耦合发电机系统：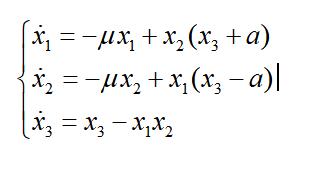

耦合系统函数：

function dx=ouhe1(t,x)

dx(1,1)=-x(4)*x(1)+x(2)*(x(3)+x(5));

dx(2,1)=-x(4)*x(2)+x(1)*(x(3)-x(5));

dx(3,1)=x(3)-x(1)*x(2);

dx(4,1)=0;

dx(5,1)=0;

分岔图程序：

clear;

clc;

Z=[];

for a=linspace(0.5,10.5,500); %舍弃前面迭带的结果，用后面的结果画图：即0.5-10.5分为500点

    [T,Y]=ode45('ouhe1',1,[1;1;1;2;a]);

    [T,Y]=ode45('ouhe1',20,Y(length(Y),:));

    Y(:,1)=Y(:,2)-Y(:,1);

    for k=2:length(Y)

        f=k-1;    

        if Y(k,1)<0  

            if Y(f,1)>0

                y=Y(k,2)-Y(k,1)*(Y(f,2)-Y(k,2))/(Y(f,1)-Y(k,1));

                Z=[Z a+abs(y)*i];

            end     

        else       

            if Y(f,1)<0

                y=Y(k,2)-Y(k,1)*(Y(f,2)-Y(k,2))/(Y(f,1)-Y(k,1));

                Z=[Z a+abs(y)*i];

            end

        end   

    end

end

plot(Z,'.','markersize',1);

title('ouhe映射分岔图');

xlabel('a'),ylabel('|y|')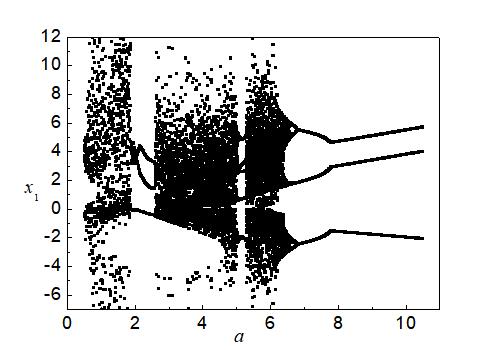

 

2.功率谱：对上面耦合系统的功率谱的研究

clear all

x=zeros(1,10001);y=zeros(1,10001);z=zeros(1,10001);%数组置零

x(1)=1;y(1)=1;z(1)=1;

h=0.001;k=10000;a=3;u=2;

for i=1:k

x(i+1)=x(i)+h*(-u*x(i)+y(i)*(z(i)+a));   %欧拉离散

y(i+1)=y(i)+h*(-u*y(i)+x(i)*(z(i)-a));

z(i+1)=z(i)+h*(z(i)-x(i)*y(i));

end

 

X1=fft(z,16384);                %对x做傅里叶变换，取8192个点

p=X1.*conj(X1)/16384;           %求x的模及功率谱密度，单位：dB 同样可求y或z

c=100*[0:8191]/16384;           %取双边，也可取单边c=[0:4095]/0.8192;            

%title('题目')                  %顶端题目

plot(c,log10(p(1:8192)),'k')%画出左半部分

 axis([0 4 -3 6]);  %限制横、纵坐标范围

%plot(c,abs(X1(1:4096)))     有时候也可用x的绝对值表示功率大小，没求对数

xlabel('\\itf\\rm/HZ','fontsize',18,'fontName','times new Roman','fontweight','bold','color','k'); %加横坐标,\\it表倾斜，\\rm表复正

ylabel('power spectrum/dB','fontsize',18,'fontName','times new Roman','fontweight','bold','color','k');  %纵坐标标示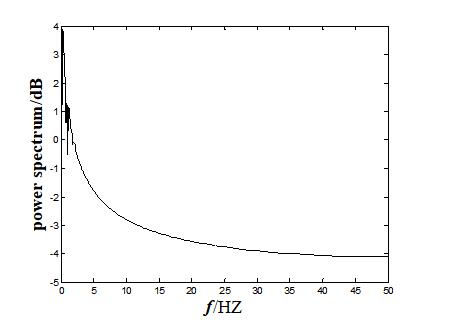

3.最大李雅谱指数程序：仍对上述耦合系统

clear;  %与ouhe系统的分岔图（fotran）符合的很好

clc;

d0=1e-8;

le=0;

lsum=0;

x=1;

y=1;

z=1;

x1=1;

 

y1=1;

z1=1+d0;

for i=1:500   

    [T1,Y1]=ode45('ouhe1',[0,1],[x;y;z;4.05;7.0]);   

    [T2,Y2]=ode45('ouhe1',[0,1],[x1;y1;z1;4.05;7.0]);   

    n1=length(Y1);

    n2=length(Y2);

    x=Y1(n1,1);

    y=Y1(n1,2);

    z=Y1(n1,3);

    x1=Y2(n2,1);

    y1=Y2(n2,2);

    z1=Y2(n2,3);

    d1=sqrt((x-x1)^2+(y-y1)^2+(z-z1)^2);

    x1=x+(d0/d1)*(x1-x);

    y1=y+(d0/d1)*(y1-y);

    z1=z+(d0/d1)*(z1-z);

    if i>100

        lsum=lsum+log(d1/d0);   

    end

end

        le=lsum/(i-100)

最大李雅谱指数谱程序：仍对上述耦合系统

clear; %可调参数区间和步长，如a的第5和36行

clc;

LE1=[];

d0=1e-8;

for a=linspace(0.5,10.5,300);

   le=0;

   lsum=0;

   x=1;

   y=1;

   z=1;

   x1=1;

   y1=1;

   z1=1+d0;

 for i=1:150   

    [T1,Y1]=ode45('ouhe1',[0,1],[x;y;z;2;a]);   

    [T2,Y2]=ode45('ouhe1',[0,1],[x1;y1;z1;2;a]);   

    n1=length(Y1);

    n2=length(Y2);

    x=Y1(n1,1);

    y=Y1(n1,2);

    z=Y1(n1,3);

    x1=Y2(n2,1);

    y1=Y2(n2,2);

    z1=Y2(n2,3);

    d1=sqrt((x-x1)^2+(y-y1)^2+(z-z1)^2);

    x1=x+(d0/d1)*(x1-x);

    y1=y+(d0/d1)*(y1-y);

    z1=z+(d0/d1)*(z1-z);

     if i>50

        lsum=lsum+log(d1/d0);   

     end

  end

        le=lsum/(i-50);

        LE1=[LE1 le];

end  

        a=linspace(0.5,10.5,300);

        plot(a,LE1,'-');

        title('largest Lyapunov exponents of ouhe1');

        xlabel('parameter a'),ylabel('largest Lyapunov exponents');

        grid    

双参数空间的最大李雅谱指数谱程序：仍对以上耦合系统

clear; %可调参数区间和步长

clc;

global u a

N1=linspace(0,0,200);

N2=linspace(0,0,400);

for I=1:200

    u=1.5+I*0.025;

      d0=1e-8;

   for L=1:400

       a=0.5+L*0.025;

          le=0;

          lsum=0;

          x=1;

          y=1;

          z=1;

          x1=1;

          y1=1;

          z1=1+d0;

      for i=1:150   

         [T1,Y1]=ode45('ouhe1',[0,1],[x;y;z;u;a]);   

         [T2,Y2]=ode45('ouhe1',[0,1],[x1;y1;z1;u;a]);   

         n1=length(Y1);

         n2=length(Y2);

         x=Y1(n1,1);

         y=Y1(n1,2);

         z=Y1(n1,3);

         x1=Y2(n2,1);

         y1=Y2(n2,2);

         z1=Y2(n2,3);

         d1=sqrt((x-x1)^2+(y-y1)^2+(z-z1)^2);

         x1=x+(d0/d1)*(x1-x);

         y1=y+(d0/d1)*(y1-y);

         z1=z+(d0/d1)*(z1-z);

        if i>50

          lsum=lsum+log(d1/d0);   

        end

      end

           le=lsum/(i-50);

           LE1(I,L)=le;

           N2(L)=a;

   end

     N1(I)=u;



end   



   [X,Y]=meshgrid(N1,N2);

   Z=LE1;

   pcolor(X,Y,Z); %画伪彩图

   %colormap jet,shading interp %连续变化的变异饱和色图，表面画伪彩图

   %contourf(X,Y,Z)%画等高线

     

 title('largest Lyapunov exponents of ouhe1')

 xlabel('parameter \\itu')

 ylabel('parameter \\ita')

 zlabel('最大李雅普指数\\delta','FontSize',12)

4.李雅谱指数程序：仍对以上耦合系统

clear;

clc;

x=1;

y=1;

z=1;

h=0.003;

a=3.5;u=2;

V=eye(3);

S=V;

b1=0;

k=50000;

for i=1:k   

    x1=x+h*(-u*x+y*(z+a));    

    y1=y+h*(-u*y+x*(z-a));    

    z1=z+h*(z-x*y);

    x=x1;y=y1;z=z1;   

    J=[-u  a+z   y    

       z-a  -u   x    

       -y   -x   1];   

           

    J=eye(3)+h*J;    

    B=J*V*S;    

    [V,S,U]=svd(B);

    a_max=max(diag(S));

    S=(1/a_max)*S;    

    b1=b1+log(a_max);

end

Lyapunov=(log(diag(S))+b1)/(k*h)

李雅谱指数谱程序：仍对以上耦合系统

clear;%奇异值分解法计算ouhe系统的李雅普诺夫指数谱

clc;

Z1=[];

Z2=[];

Z3=[];

x=1;

y=1;

z=1;

h=0.002;

u=2;

%a=3;

k=10000;

for a=linspace(0.5,10.5,1000);

    V=eye(3);

    S=V;

    b1=0;

    lp=0;

  for i=1:k   

   x1=x+h*(-u*x+y*(z+a));    

    y1=y+h*(-u*y+x*(z-a));    

    z1=z+h*(z-x*y);

    x=x1;y=y1;z=z1;   

    J=[-u  a+z   y    

       z-a  -u   x    

       -y   -x   1];   

           

    J=eye(3)+h*J;    

    B=J*V*S;    

    [V,S,U]=svd(B);

    a_max=max(diag(S));

    S=(1/a_max)*S;    

    b1=b1+log(a_max);



  end

    lp=(log(diag(S))+b1)/(k*h);

    Z1=[Z1 lp(1)];

    Z2=[Z2 lp(2)];

    Z3=[Z3 lp(3)];

     

end

     a=linspace(0.5,10.5,1000);

    plot(a,Z1,'-',a,Z2,'-',a,Z3,'-');

    title('Lyapunov exponents of ouhe');

    xlabel('parameter a'),ylabel('lyapunov exponents');

grid on

6.三维、二维以及时间序列图：

耦合系统的函数程序：

function dx=ouhe(t,x)

dx=zeros(3,1);

a=3;u=2;

dx(1)=-u*x(1)+x(2)*(x(3)+a);

dx(2)=-u*x(2)+x(1)*(x(3)-a);

dx(3)=x(3)-x(1)*x(2);

图程序：

clc;

clear;

[t,x]=ode45('ouhe',[0 1000],[1 -1 1]);

subplot(2,2,1); plot(x(:,1),'k','markersize',0.5);

xlabel('t/ms','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

ylabel('x','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

subplot(2,2,2); plot(x(:,2),'k','markersize',0.5);

xlabel('t/ms','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

ylabel('y','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

subplot(2,2,3); plot(x(:,3),'k','markersize',0.5);

xlabel('t/ms','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

ylabel('z','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

subplot(2,2,4); plot3(x(:,1),x(:,2),x(:,3),'k','markersize',0.5);grid on;

xlabel('x','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

ylabel('y','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

zlabel('z','fontsize',12,'fontName','times new Roman','fontweight','bold','color','k');

figure(2);plot3(x(:,1),x(:,2),x(:,3),'k','markersize',0.5);grid on;

xlabel('\\itx\\rm_1','fontsize',20,'fontName','times new Roman','fontweight','bold','color','k');

ylabel('\\itx\\rm_2','fontsize',20,'fontName','times new Roman','fontweight','bold','color','k');

zlabel('\\itx\\rm_3','fontsize',20,'fontName','times new Roman','fontweight','bold','color','k');

取参数a=3:0.001:4,迭代初值x(0)=0.1，计算Logistic映射的Lyapunov指数，并做可视化呈现

clear all;
hold on
alpha0=3:0.001:4;
N=1000;
for j=1:length(alpha0
alpha=alpha0(j);
x0=0.1;%初始值
s=0;
for ii=1:N
df=alpha-2*alpha*x0;
s=s+log(abs(df));%lambda叠加
x0=alpha*x0*(1-x0);%x迭代
end
Lm(j)=s/N;% 指数
end
plot(alpha0,Lm,'r')

N维离散系统动力学Mapping的分岔图与李雅普诺夫指数计算

clear all;

clc



a=4;

b1=1;

b2=1;

d=0.5;

c1=1.08;

c2=1;

z=0.5;

m=0.25;

p=0.5;

T=0.1;

S=0.1;

k2=0.15;



N1 = 100;

N2 = 400;

k10 = 0:0.001:0.4;

f = zeros(N1+N2,length(k10));

f2 = zeros(N1+N2,length(k10));





for kk=1:length(k10)

    x0=2.5;

    y0=2.35;

    k1=k10(kk)

    L1=0;L2=0;

    %     s=zeros(2,1);

    J1=eye(2);

    for j = 1:N1+N2

        x1=x0+ k1.*x0.*(a-2*b1.*x0+d.*y0+b1.*(c1+(1-m).*z-S));

        y1=y0+ k2.*y0.*(a-2*b2.*y0+d.*x0+b2.*(c2-p.*m.*z+T));

        f(j,kk) =x1;

        f2(j,kk) =y1;

        j1=1 + a*k1 + d*k1*y1 + b1*k1 *(c1 - S - 4*x1 + z - m*z);

        j2=d*k1*x1;

        j3=d*k2*y1;

        j4=1 + a*k2 + d *k2 *x1 + b2 *k2 *(c2 + T - 4 *y1 - m *p* z);

        x0=x1;y0=y1;

    end

end



hold on

f = f(N1+1:end,:);

plot(k10,f,'b.','MarkerSize',1)

ylabel('Price');



hold on

f2 = f2(N1+1:end,:);

plot(k10,f2,'r.','MarkerSize',1)

xlabel('\\mu');

ylabel('Price');



% plot(k10,Lm2,'r','linewidth',0.5)

plot(k10,Lm1,'b')

line([0 0.4],[0 0])

=0 临界点

<0稳定 >0不稳定，分叉