数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质示例 )
Posted 韩曙亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质示例 )相关的知识,希望对你有一定的参考价值。
文章目录
一、傅里叶变换时移性质
傅里叶变换频移性质 :
" 序列信号 x ( n ) x(n) x(n) " 的 " 傅里叶变换 A " ,
" 序列信号 x ( n ) x(n) x(n) " 与 " 单位复指数 e j ω 0 n e^j \\omega_0 n ejω0n " 相乘 , 得到的 " 序列 B " ,
注意这里的 单位复指数 中的 ω 0 \\omega_0 ω0 就是 傅里叶变换 中的移位 ,
求该 " 序列 B " 的 " 傅里叶变换 C " ,
" 傅里叶变换 A " 与 " 傅里叶变换 C " 这两个频域信息形状相同 , 位移相差 ω 0 \\omega_0 ω0 ;
也就是说
" 傅里叶变换 A " 移位 ω 0 \\omega_0 ω0 后, 得到 " 傅里叶变换 C " ;
使用公式表示为 :
S F T [ e j ω 0 n x ( n ) ] = X ( e j ( ω − ω 0 ) ) SFT[e^j \\omega_0 nx(n)] = X(e^j ( \\omega - \\omega_0 )) SFT[ejω0nx(n)]=X(ej(ω−ω0))
二、傅里叶变换时移性质示例
已知序列
x 1 ( n ) = 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 x_1(n)=\\1,2,3,4,5,6,7,8,9,9,8,7,6,5,4,3,2,1\\ x1(n)=1,2,3,4,5,6,7,8,9,9,8,7,6,5,4,3,2,1
x 2 ( n ) x_2(n) x2(n) 序列 是 x 1 ( n ) x_1(n) x1(n) 序列 乘以 " 单位复指数 " e j ω 0 n e^j \\omega_0 n ejω0n , 其中 ω 0 = π 2 \\omega_0 = \\cfrac\\pi2 ω0=2π , 表示为 :
x 2 ( n ) = x 1 ( n ) e j π n / 2 x_2(n) = x_1(n ) e^j \\pi n / 2 x2(n)=x1(n)ejπn/2
x 1 ( n ) = 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 x_1(n)=\\1,2,3,4,5,6,7,8,9,9,8,7,6,5,4,3,2,1\\ x1(n)=1,2,3,4,5,6,7,8,9,9,8,7,6,5,4,3,2,1 序列的 " 幅频特性 " , 即 x 1 ( n ) x_1(n) x1(n) 的傅里叶变换取模 :
∣ X 1 ( e j ω ) ∣ |X_1(e^j\\omega)| ∣X1(ejω)∣
如下图所示 :

x 2 ( n ) x_2(n) x2(n) 序列的 " 幅频特性 " , 即 x 2 ( n ) x_2(n) x2(n) 的傅里叶变换取模 :
∣ X 2 ( e j ω ) ∣ |X_2(e^j\\omega)| ∣X2(ejω)∣
如下图所示 :
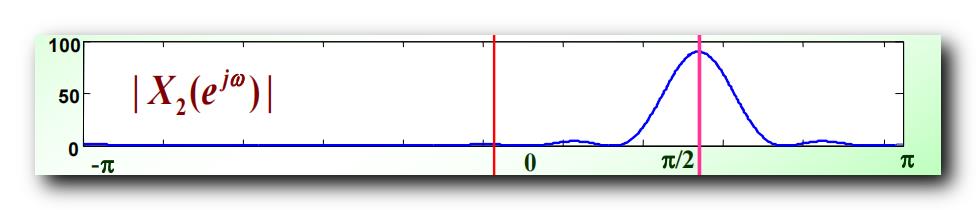
x 2 ( n ) = x 1 ( n ) e j π n / 2 x_2(n) = x_1(n ) e^j \\pi n / 2 x2(n)=x1(n)ejπn/2 序列相对于 x 1 ( n ) x_1(n) x1(n) 序列 , 其 傅里叶变换 平移了 π 2 \\cfrac\\pi2 2π ;
x 1 ( n ) x_1(n) x1(n) 和 x 2 ( n ) x_2(n) x2(n) 幅频特性 相差 π 2 \\cfrac\\pi2 2π ;
根据 " 傅里叶变换频移性质 " , x 2 ( n ) x_2(n) x2(n) 的幅频特性 , 相对于 x 1 ( n ) x_1(n) x1(n) 的幅频特性 , 向右平移了 π 2 \\cfrac\\pi2 2π 单位 ;
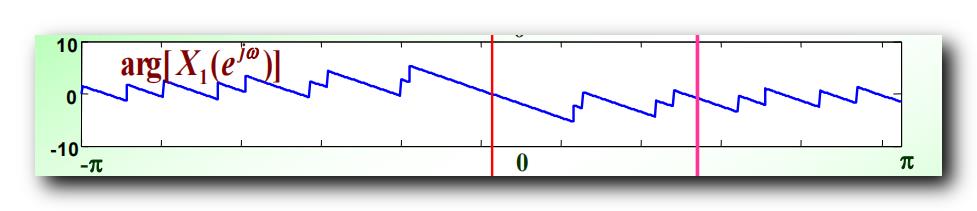
x 1 ( n ) x_1(n) x1(n) 的 " 相频特性 " 如下 :
x 2 ( n ) x_2(n) x2(n) 的 " 相频特性 " 如下 :

x 2 ( n ) = x 1 ( n ) e j π n / 2 x_2(n) = x_1(n ) e^j \\pi n / 2 x2(n)=x1(n)ejπn/2 序列相对于 x 1 ( n ) x_1(n) x1(n) 序列 , 其 傅里叶变换 平移了 π 2 \\cfrac\\pi2 2π ;
x 1 ( n ) x_1(n) x1(n) 和 x 2 ( n ) x_2(n) x2(n) 相频特性 相差 π 2 \\cfrac\\pi2 2π ;
根据 " 傅里叶变换频移性质 " , x 2 ( n ) x_2(n) x2(n) 的相频特性 , 相对于 x 1 ( n ) x_1(n) 以上是关于数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质示例 )的主要内容,如果未能解决你的问题,请参考以下文章
数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质 | 证明过程 )
数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质 | 证明过程 )
数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质示例 | PCM 音频信号处理 | 使用 matlab 进行频移操作 )
数字信号处理傅里叶变换性质 ( 傅里叶变换频移性质示例 | PCM 音频信号处理 | 使用 matlab 进行频移操作 )