蓝桥杯 K倍区间 python

Posted 2022-02-08 风信子的猫Redamancy

蓝桥杯 K倍区间 python

题目描述

给定一个长度为 NN 的数列，$A_1,A_2,\cdots A_N$​​​，如果其中一段连续的子序列 $A_i,A_i+1,\\cdots A_j(i\\leq j) $​之和是 KK 的倍数，我们就称这个区间 [i, j][i,j] 是 K 倍区间。

你能求出数列中总共有多少个 KK 倍区间吗？

输入描述

第一行包含两个整数 N 和 K$(1\le N,K\le 10^5)$

以下 N 行每行包含一个整数 $A_i(1\le A_i\le 10^5)$​

输出描述

输出一个整数，代表 K 倍区间的数目。

输入输出样例

示例

输入

5 2
1
2
3
4
5

输出

6

运行限制

• 最大运行时间：2s
• 最大运行内存: 256M

解题思路

思路也很简单，简单来说，就是得到每一个和，我们可以利用前缀来求，比如我们得到了一个sum的数组，[i,j]区间的和也就是sum[j] - sum[i-1]，这样我们就可以得到我们的和，然后判断和是否能够%K为0，如果能就计数+1

但是毫无疑问，这样做是一定会TLE的，无法AC的

看了一些大佬的思路，这里面用了一些数学的知识

当区间和对K取模等于0即 ( sum[j]-sum[i-1] )%K= 0 ( 化为sum[j]%K=sum[i-1] %K ) 时此区间满足条件要求。

所以对每个sum[i]，求其值时顺求其对K的取模，最后得到一模数列，方便计算。

得到模数列，需选取模数列中的相同模进行组合，但题目限制了时空复杂度，此行不可行。

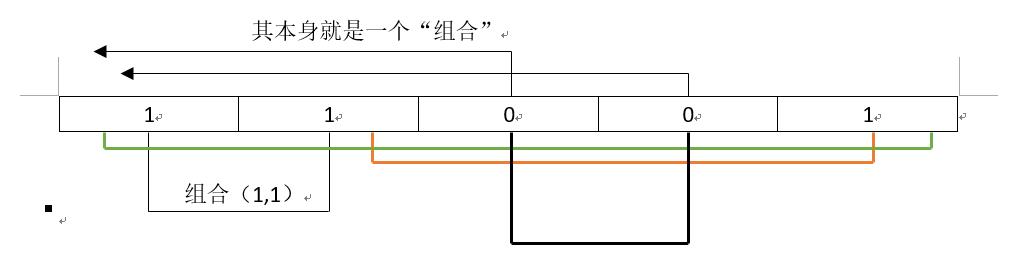
以题目中的第一个测试用例为例，求得模数列为 1 1 0 0 1

手动组合体验一下组合过程：

首元素 1 本身组合不了

第二个 1 可以与前面一个 1 组合

第三个元素 0 本身组合不了

第四个元素 0 可以与第三个元素 0 组合

第五个元素 1 可以与前面两个1 组合两次。（可以看出只要迭代加上前面已经出现过的相同模即可，假如存在第六个元素 1 ，此时它前面有 3 个 模 1 ，它可以与他们3个一一组合，一共在3种情况，所以加上3即可）

注意：模为0的情况，其本身不需要和其他0进行组合，因为他们不用和其他模相等（相减），自己这个数列本身就满足K倍。

代码

import os
import sys

# 请在此输入您的代码
N,K = map(int,input().split())
ans = 0
cnt = [0]*K

for i in range(N):
  num = int(input())
  ans += num
  cnt[ans%K] += 1

ans = cnt[0]
for i in range(0,K):
  if cnt[i]:
    ans += cnt[i] * (cnt[i] - 1)//2

print(ans)

有时候，可能在看题解的时候，会发现有人把 $cnt[0]$​​ 设为1，直接初始化为1进行求解，得到的结果是正确的，这也涉及到一些数学知识，在前面的思路过程中，我们说，我们需要对模为0的直接进行一个加和，比如说，模为0的有m个，他们的组合是 $C_m^2$​​ 个，由于模为0本身也是一种情况，所以说，得到的组合和本身就是 $C_m^2+m$​​ 个，这里我们就可以有一个数学的公式转化
$$C_m^2+m=\frac{m\ast (m-1)}{2}+m=m(\frac{m-1}{2}+1)=\frac{(m+1)\ast m}{2}=C_{m+1}^2$$

所以对于我们的计算来说，我们可以一开始就将第一个置为0，我们也可以进行加和，两者结果是相等的