Tensor：Pytorch神经网络界的Numpy

Posted 2022-01-21 李元静

目录

• Tensor
• • 创建Tensor
  • 修改Tensor维度
  • 截取元素
  • 简单的数学运算
  • 归并操作
  • 比较操作
  • 矩阵运算

Tensor

Tensor，它可以是0维、一维以及多维的数组，你可以将它看作为神经网络界的Numpy，它与Numpy相似，二者可以共享内存，且之间的转换非常方便。

但它们也不相同，最大的区别就是Numpy会把ndarray放在CPU中进行加速运算，而由Torch产生的Tensor会放在GPU中进行加速运算。

对于Tensor，从接口划分，我们大致可分为2类：

1. torch.function：如torch.sum、torch.add等。
2. tensor.function：如tensor.view、tensor.add等。

而从是否修改自身来划分，会分为如下2类：

1. 不修改自身数据，如x.add(y)，x的数据不变，返回一个新的Tensor。
2. 修改自身数据，如x.add_(y)，运算结果存在x中，x被修改。

简单的理解就是方法名带不带下划线的问题。

现在，我们来实现2个数组对应位置相加，看看其效果就近如何：

import torch

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
print(x + y)
print(x.add(y))
print(x)
print(x.add_(y))
print(x)

运行之后，效果如下：

下面，我们来正式讲解Tensor的使用方式。

创建Tensor

与Numpy一样，创建Tensor也有很多的方法，可以自身的函数进行生成，也可以通过列表或者ndarray进行转换，同样也可以指定维度等。具体方法如下表（数组即张量）：

函数	意义
Tensor(*size)	直接从参数构造，支持list，Numpy数组
eye(row,column)	创建指定行列的二维Tensor
linspace(start,end,steps)	从start到end，均匀切分成steps份
logspace(start,end,steps)	从10^start到10^and，均分成steps份
rand/randn(*size)	生成[0,1)均匀分布/标准正态分布的数据
ones(*size)	生成指定shape全为1的张量
zeros(*size)	生成指定shape全为0的张量
ones_like(t)	返回与t的shape相同的张量，且元素全为1
zeros_like(t)	返回与t的shape相同的张量，且元素全为0
arange(start,end,step)	在区间[start,end)上，以间隔step生成一个序列张量
from_Numpy(ndarray)	从ndarray创建一个Tensor

这里需要注意Tensor有大写的方法也有小写的方法，具体效果我们先来看看代码：

import torch

t1 = torch.tensor(1)
t2 = torch.Tensor(1)
print("值0,类型1".format(t1, t1.type()))
print("值0,类型1".format(t2, t2.type()))

运行之后，效果如下：

可以看到，tensor与Tensor生成的值的类型就不同，而且t2（Tensor）返回一个大小为1的张量，而t1（tensor）返回的就是1这个值。

其他示例如下：

import torch
import numpy as np

t1 = torch.zeros(1, 2)
print(t1)
t2 = torch.arange(4)
print(t2)
t3 = torch.linspace(10, 5, 6)
print(t3)
nd = np.array([1, 2, 3, 4])
t4 = torch.from_numpy(nd)
print(t4)

其他例子基本与上面基本差不多，这里不在赘述。

修改Tensor维度

同样的与Numpy一样，Tensor一样有维度的修改函数，具体的方法如下表所示：

函数	意义
size()	返回张量的shape，即维度
numel(input)	计算张量的元素个数
view(*shape)	修改张量的shape，但View返回的对象与源张量共享内存，修改一个，另一个也被修改。Reshape将生成新的张量，而不要求源张量是连续的，View(-1)展平数组
resize	类似与view，但在size超出时，会重新分配内存空间
item	若张量为单元素，则返回Python的标量
unsqueeze	在指定的维度增加一个“1”
squeeze	在指定的维度压缩一个“1”

示例代码如下所示：

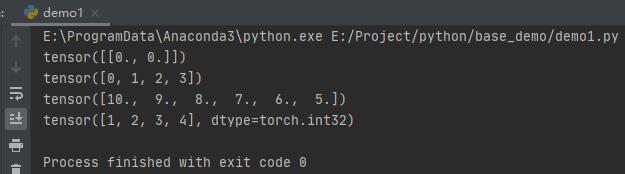
import torch

t1 = torch.Tensor([[1, 2]])
print(t1)
print(t1.size())
print(t1.dim())
print(t1.view(2, 1))
print(t1.view(-1))
print(torch.unsqueeze(t1, 0))
print(t1.numel())

运行之后，效果如下：

截取元素

当然，我们创建Tensor张量，是为了使用里面的数据，那么就不可避免的需要获取数据进行处理，具体截取元素的方式如表：

函数	意义
index_select(input,dim,index)	在指定维度选择一些行或者列
nonzero(input)	获取非0元素的下标
masked_select(input,mask)	使用二元值进行选择
gather(input,dim,index)	在指定维度上选择数据，输出的维度与index一致（index的类型必须是LongTensor类型的）
scatter_(input,dim,index,src)	为gatter的反操作，根据指定索引补充数据(将src中数据根据index中的索引按照dim的方向填进input中)

示例代码如下所示：

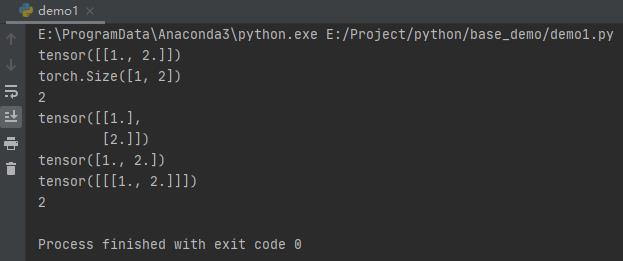
import torch

# 设置随机数种子，保证每次运行结果一致
torch.manual_seed(100)
t1 = torch.randn(2, 3)
# 打印t1
print(t1)
# 输出第0行数据
print(t1[0, :])
# 输出t1大于0的数据
print(torch.masked_select(t1, t1 > 0))
# 输出t1大于0的数据索引
print(torch.nonzero(t1))
# 获取第一列第一个值，第二列第二个值，第三列第二个值为第1行的值
# 获取第二列的第二个值，第二列第二个值，第三列第二个值为第2行的值
index = torch.LongTensor([[0, 1, 1], [1, 1, 1]])
# 取0表示以行为索引
a = torch.gather(t1, 0, index)
print(a)
# 反操作填0
z = torch.zeros(2, 3)
print(z.scatter_(1, index, a))

运行之后，效果如下：

我们a = torch.gather(t1, 0, index)对其做了一个图解，方便大家理解。如下图所示：

当然，我们直接有公司计算，因为这么多数据标线实在不好看，这里博主列出转换公司供大家参考：

当dim=0时,out[i,j]=input[index[i,j]][j]
当dim=1时,out[i,j]=input[i][index[i][j]]

简单的数学运算

与Numpy一样，Tensor也支持数学运算。这里，博主列出了常用的数学运算函数，方便大家参考：

函数	意义
abs/add	绝对值/加法
addcdiv(t,v,t1,t2)	t1与t2逐元素相除后，乘v加t
addcmul(t,v,t1,t2)	t1与t2逐元素相乘后，乘v加t
ceil/floor	向上取整/向下取整
clamp(t,min,max)	将张量元素限制在指定区间
exp/log/pow	指数/对数/幂
mul(或*)/neg	逐元素乘法/取反
sigmoid/tanh/softmax	激活函数
sign/sqrt	取符号/开根号

需要注意的是，上面表格所有的函数操作均会创建新的Tensor，如果不需要创建新的，使用这些函数的下划线"_"版本。

示例如下：

t = torch.Tensor([[1, 2]])
t1 = torch.Tensor([[3], [4]])
t2 = torch.Tensor([5, 6])
# t+0.1*(t1/t2)
print(torch.addcdiv(t, 0.1, t1, t2))
# t+0.1*(t1*t2)
print(torch.addcmul(t, 0.1, t1, t2))
print(torch.pow(t,3))
print(torch.neg(t))

运行之后，效果如下：

上面的这些函数都很好理解，只有一个函数相信没接触机器学习的时候，不大容易理解。也就是sigmoid()激活函数，它的公式如下：

归并操作

简单的理解，就是对张量进行归并或者说合计等操作，这类操作的输入输出维度一般并不相同，而且往往是输入大于输出维度。而Tensor的归并函数如下表所示：

函数	意义
cumprod(t,axis)	在指定维度对t进行累积
cumsum	在指定维度对t进行累加
dist(a,b,p=2)	返回a,b之间的p阶范数
mean/median	均值/中位数
std/var	标准差/方差
norm(t,p=2)	返回t的p阶范数
prod(t)/sum(t)	返回t所有元素的积/和

示例代码如下所示：

t = torch.linspace(0, 10, 6)
a = t.view((2, 3))
print(a)
b = a.sum(dim=0)
print(b)
b = a.sum(dim=0, keepdim=True)
print(b)

运行之后，效果如下：

需要注意的是，sum函数求和之后，dim的元素个数为１，所以要被去掉，如果要保留这个维度，则应当keepdim=True，默认为False。

比较操作

在量化交易中，我们一般会对股价进行比较。而Tensor张量同样也支持比较的操作，一般是进行逐元素比较。具体函数如下表：

函数	意义
equal	比较张量是否具有相同的shape与值
eq	比较张量是否相等，支持broadcast
ge/le/gt/lt	大于/小于比较/大于等于/小于等于比较
max/min(t,axis)	返回最值，若指定axis，则额外返回下标
topk(t,k,dim)	在指定的dim维度上取最高的K个值

示例代码如下所示：

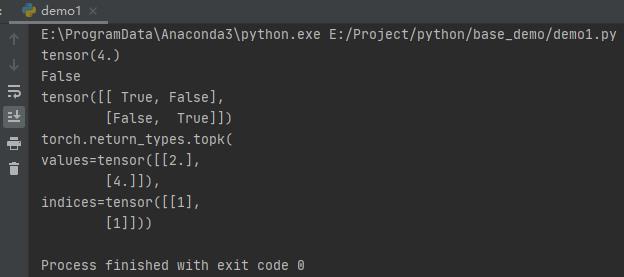
t = torch.Tensor([[1, 2], [3, 4]])
t1 = torch.Tensor([[1, 1], [4, 4]])
# 获取最大值
print(torch.max(t))
# 比较张量是否相等
# equal直接返回True或False
print(torch.equal(t, t1))
# eq返回对应位置是否相等的布尔值与两者维度相同
print(torch.eq(t, t1))
# 取最大的2个元素，返回索引与值
print(torch.topk(t, 1, dim=0))

运行之后，输出如下：

矩阵运算

机器学习与深度学习中，存在大量的矩阵运算。与Numpy一样常用的矩阵运算一样，一种是逐元素相乘，一种是点积乘法。函数如下表所示：

函数	意义
dot(t1,t2)	计算t1与t2的点积，但只能计算1维张量
mm(mat1,mat2）	计算矩阵乘法
bmm(tatch1,batch2)	含batch的3D矩阵乘法
mv(t1,v1)	计算矩阵与向量乘法
t	转置
svd(t)	计算t的SVD分解

这里有3个主要的点积计算需要区分，dot()函数只能计算1维张量，mm()函数只能计算二维的张量，bmm只能计算三维的矩阵张量。示例如下：

# 计算1维点积
a = torch.Tensor([1, 2])
b = torch.Tensor([3, 4])
print(torch.dot(a, b))
# 计算2维点积
a = torch.randint(10, (2, 3))
b = torch.randint(6, (3, 4))
print(torch.mm(a, b))
# 计算3维点积
a = torch.randint(10, (2, 2, 3))
b = torch.randint(6, (2, 3, 4))
print(torch.bmm(a, b))

运行之后，输出如下：