Java版高级数据结构树论基础&二叉树

Posted 2022-01-15 chenry777

本文涉及代码见博主的github : https://github.com/chenruoyu0319/data-structure-for-java/tree/main/%E6%A0%91%E8%AE%BA%E5%9F%BA%E7%A1%80

一、树的定义

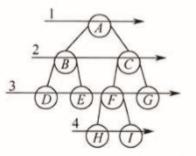
上图中，123都是数，4是图

在树形结构里面有几个重要的术语：

1.结点：树里面的元素。

2.父子关系：结点之间相连的边

3.子树：当结点大于1时，其余的结点分为的互不相交的集合称为子树

4.度：一个结点拥有的子树数量称为结点的度（用于区分叶子节点）

5.叶子：度为0的结点

6.孩子：结点的子树的根称为孩子结点

7.双亲：和孩子结点对应

8.兄弟：同一个双亲结点

9.森林：由N个互不相交的树构成深林

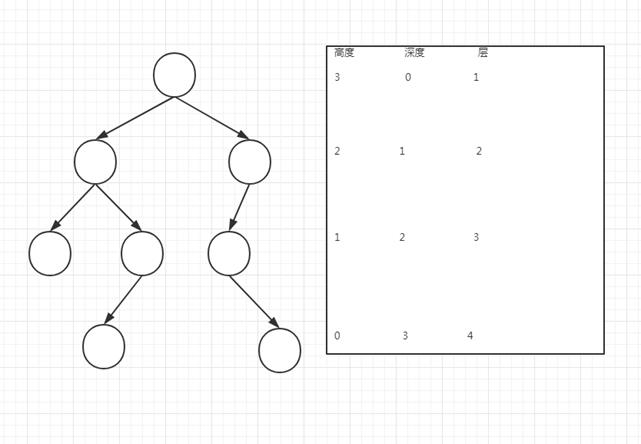
结点的高度：结点到叶子结点的最长路径

结点的深度：根结点到该结点的边个数

结点的层数：结点的深度加1

树的高度：根结点的高度

二、二叉树（Binary Tree）

在树形结构中最重要的就是二叉树，很多经典的算法与数据结构其实都是通过二叉树发展而来。二叉树是一种特殊的树形结构，每个节点至多只有两颗子树，在二叉树的第N层上至多有2^(N-1)个结点。几个常见的二叉树:

平衡二叉树

二叉查找树

红黑树

完全二叉树：除最后一层外，其他的结点个数必须达到最大，并且最后一层结点都连续靠左排列。可以用于堆排序；大顶堆，小顶堆；

满二叉树：除叶子结点外，每个结点都有左右两个子结点。

三、思考？为什么要分满二叉树和完全二叉树呢？

因为通过定义可以看出，完全二叉树只是满二叉树里面的一个子集

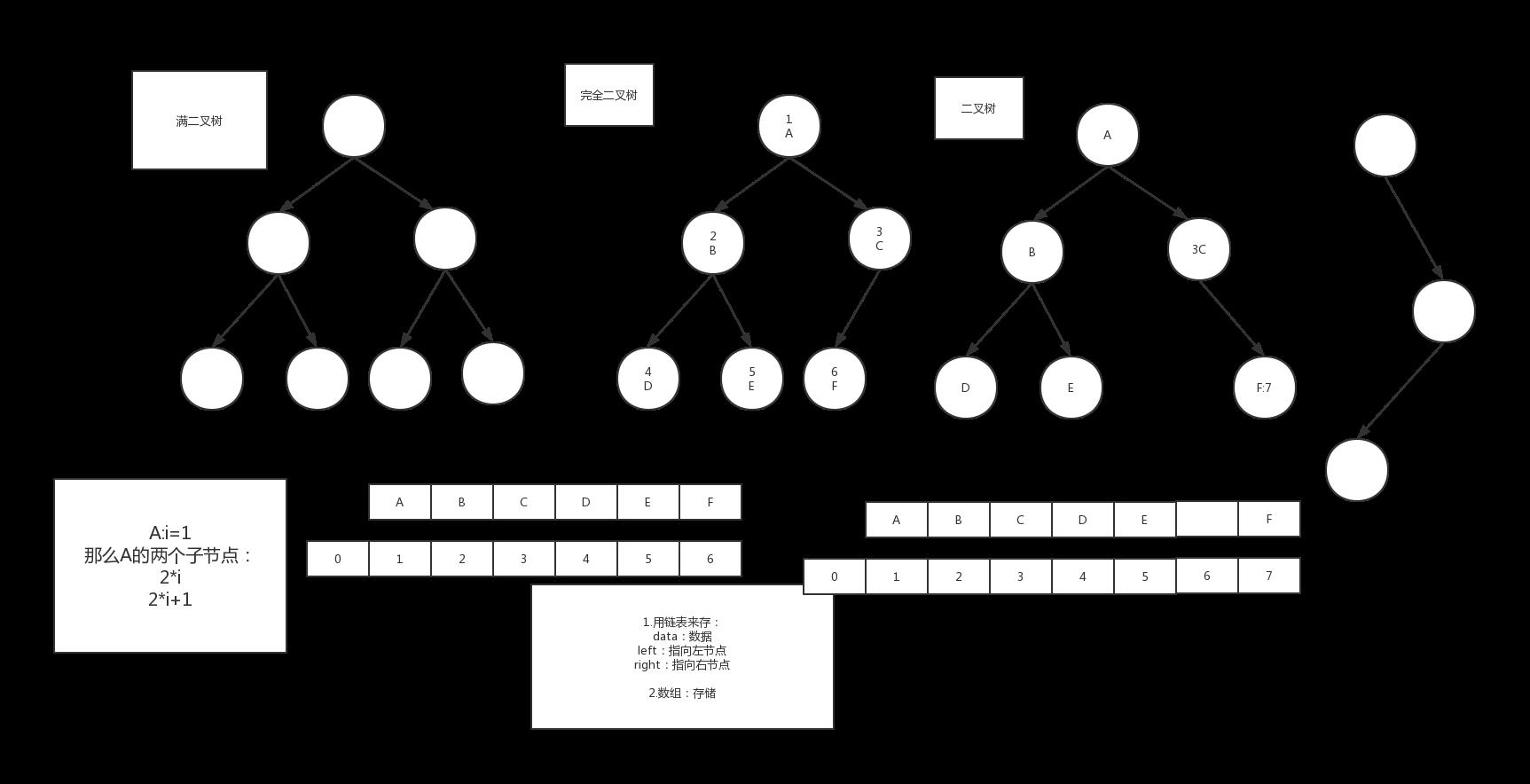
要想清楚上面那个问题我们要从树形结构的存储开始：下面是一个完全二叉树

因为数组的遍历速度远大于链表，所以我们肯定要优先考虑能否基于数组存储：例如完全二叉树，我们就可以利用数组下标来实现对它的遍历。假设A为i，则B=2*i,C=2*i+1，依次类推

但是假如是下面第二图这种情况，用数组存储会发生什么情况？

你会发现如果用数组来存储的话会浪费很多空间(有些空间实际上没有存储数据)，那怎么办呢？大家最先想到的肯定是链表，对的，

是要借用链表来实现，但是数组的性能是高效的，也不需要开额外的指针，所以如果是一课完全

二叉树的话我们就可以用数组来实现，这也是为什么还要分一个完全二叉树出来的根本原因。

后面的堆还会在来看这个结构。

完全二叉树用数组存储的分析过程：

四、二叉树的遍历

对于一种二叉树，通常有四种遍历方式：前序、中序、后序、层次

遍历的原则：所有的遍历都是以根节点为基准点

重要口诀：根节点输出！每次递归都是一颗新的子树。也可以理解成按口诀顺序输出。左边如果有就走左边，左边没有就输出根走右边。其中根，就是每一个子树的开始 。

比如上图，每次进行的循环路径走下面的分叉，每次递完一条分叉就归到A

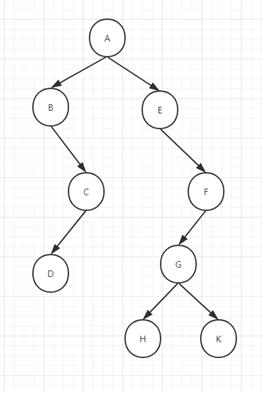
前序：根 左 右 ABCDEFGHK

中序：左 根 右 BDCAEHGKF

后序：左 右 根 DCBHKGFEA

层次：ABECFDGHK

如何实现层次遍历？进行层次遍历需要一个队列。先将二叉树根结点入队，然后出队，访问该结点，若它有左子树，则将左子树根结点入队；若它有右子树，则将右子树根结点入队。然后出队，对出队结点访问，如此反复，直到队列空。

五、由遍历序列构造二叉树

由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树。

由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树。

由二叉树的层次序列和中序序列也可以唯一地确定一棵二叉树。

由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树。

由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树。

由二叉树的层次序列和中序序列也可以唯一地确定一棵二叉树。

这告诉我们一个道理：想要利用遍历序列来唯一确定地构造一棵二叉树，中序序列是必不可少的。