经典折半查找算法

Posted 2022-01-15 Maynor大数据

本文完整阅读需要的基础知识：循环结构，数组，函数，递归。

n个由小到大排好序的数,再给一个数x,判断这个数在数组中有没有出现过,如果有,就输出这个数在数组的位置,没有就输出”NO”. 样例:输入:
6 //以下有6个数 1 4 6 8 9 10 9 //要找的x
输出: 5 //第5个数 方法:如果采用顺序查找,要经过5次才找到。
而用折半查找,开始的比较区间是1-6, 先取中间一个数,即第3个数6,
9比6大,说明在6的后面,下面就把区间变成4-6,
取中间数,即第5个数9,正好找到,这样总次数变成2次查找。

现在我们要完成这样的任务：如何在数组a的区间[first,last]内寻找key，其中a数组是有序的， 我们假设非降次序的（即：a[ first ] <= a[ first+1 ] <= … <= a[ last ] ） 中搜索key， 找到key时返回其在数组中的位置，否则返回-1 。

顺序查找（从头到尾查找一遍）

int binarySearch(int a[], int first int last, int key) 
	for (int i=first; i<=last; i++)
		if (a[i]==key) return i;
	return -1;

普通的二分查找（非递归）

int binarySearch(int a[] , int first, int last, int key) 
	int left = first;
	int right = last;
	while (left <= right) 
		int mid = (left + right)/2;  // mid = left + ((right- left) / 2);
		if (key == a[mid]) 
                      return mid;
		else if (a[mid] < key ) 
                      left = mid + 1;
		else  if( a[mid]  > key) 
                      right = mid - 1;
	
	return -1; // 未找到key

用递归算法完成二分查找

int binarySearch(int a[], int first ,int last, int key) 
	// 找到x时返回其在数组中的位置，否则返回-1
	if ( first > last) return -1;// 未找到x
	else 
		int mid = ( first + last)/2;
		if (a[mid]==key)   
                     return mid;
		else  if ( a[mid]< key )   
                     return binarySearch(a, mid+1,last ,key);
		else if( a[mid] > key) 
                     return binarySearch( a, first, mid-1, key);
	

提醒：

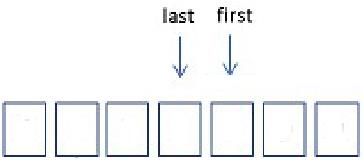
注意查找的范围【first，last】,每次查找的范围：前后都是闭区间的范围。
注意 while(first <= last)循环（递归同理）的终止条件是： first 与 last错位, 即 first == last + 1

##常犯的错误：竟然找不到某些数字
分析代码：为啥 找不到数字13呢？

#include <bits/stdc++.h>
using namespace std;
const  int  N =10;
int a[12]= 0 ,5, 13,19, 21,37,56,64,75,80,88,92;
int my_research(int L, int R, int key) 
	int first = L, last = R;
	while(first < last)     //这里有错误噢
		int middle =  (first+last)/2;
		if( a[middle]==key)
			return middle;
		else if( a[middle] < key ) 
                        first = middle+1;
		else if( a[middle] > key ) 
                        last=middle-1;
	
	return -1;


int main() 
	cout <<  my_research(1, 11,13);
	return 0;

火急提醒：while(first < last) 循环的终止条件是：first == last， 当first == last时候，【first，last】区间内还有一个值，但可惜循环已经结束了。

如果要查找有序数组里面的存在多个元素key， 要找到最左边的和最右边的位置呢？

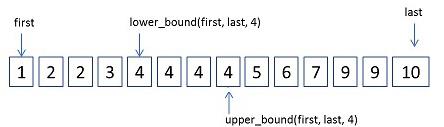
留意一下：lower_bound 和 upper_bound 分别返回哪位置。

lower_bound : 二分查找求下界

#include <bits/stdc++.h>
using namespace std;
const  int  N =10;
int a[12]= 0 ,5, 13,21, 21,21,21,64,75,80,88,92;
int my_lower_bound(int L, int R, int key) 
	int first = L, last = R;
	while(first <= last) 
		int middle =  (first+last)/2;
		if( a[middle] == key ) 
                    last = middle-1; // first 按兵不动， last移动
                else if(  a[middle] >  key  ) 
                    last = middle-1; 
		else if( a[middle] <  key )
                    first = middle+1; 
	
	return first;


int main() 
	cout <<  my_lower_bound(1, 12,21);
	return 0;

若 a[middle] ==key ,至少已经找到一个，然后左边可能还有， 因此区间变成 【first , middle】
若 a[middle] > key ,所找的位置，不可在后面, 因此区间变成【first , middle -1】
若 a[middle] < key ,所找的位置不可能是middle，也不可能在前面 因此区间变成 【middle+1， last】

upper_bound:

#include <bits/stdc++.h>
using namespace std;
const  int  N =10;
int a[12]= 0 ,5, 13,21, 21,21,21,64,75,80,88,92;
int my_upper_bound(int L, int R, int key) 
	int first = L, last = R-1;
	while(first <= last) 
                int middle =  (first+last)/2;
		if( a[middle] == key )
			first = middle+1;  // last 按兵不动，first移动
                else if( a[middle] >  key )
			last = middle-1 ;
		else if( a[middle] <  key )
			first = middle+1;
 	
	return last;


int main() 
	cout <<  my_upper_bound(1, 12,21);
	return 0;

思考：如果有序数组里面的不存在元素key

如果有序数组里面的不存在元素key

lower_bound 中的first位置停在哪里？

返回一个非递减序列 [ first, last ] 中的。当key存在多个时，返回key出现的第一个位置。 若果不存在，first停在第一个大于key的位置，即返回一个这样的下标： 在此处插入key，序列依然有序。

return ( first < length && a[first] == key ) ? first : -1;
upper_bound的last位置停在哪里呢？

返回一个非递减序列[ first, last ]中。当key存在多个时，返回key出现的最后一个位置。若果不存在， right停在第一个大于key的位置，即返回一个这样的下标： 在此处插入key，序列依然有序。

return ( last > 0 && a[last] == key ) ? last : -1;

你经常遇到的死循环

#include <bits/stdc++.h>
using namespace std;
const  int  N =10;
int a[12]= 0 ,5, 13,21, 21,21,21,64,75,80,88,92;
int wrong_lower_bound(int L, int R, int key) 
	int first = L, last = R;
	while(first <= last) 
		int middle =  (first+last)/2;
		if( a[middle] == key ) 
			last = middle; 
                else if(  a[middle] >  key  ) 
			last = middle-1; 
		else if( a[middle] <  key )
			first = middle+1; 
	
	return first;

int main() 
	cout <<  wrong_lower_bound(1, 12,21);
	return 0;

bug出现在这里： if( a[middle] == key ) last = middle; 如果first ==last ， middle = (first+last)/2 = first位置。 [first, middle] 与[fist, last]区间一样，将发生死循环。

说白了就是因为mid=（first+last）/2不会取到last值

为了这篇完整性，特地安排了这一节。具体细节日后再解析。

二分答案（不只是查找值）题目描述中若出现类似： “最大值最小”的含义，这个答案就具有单调性，可用二分答案法。这个宏观的最优化问题，可以抽象为一个函数，其“定义域”是该问题的可行方案。

满足 >=x的范围中查找最小的一个

考虑“求某个条件C(x)的最小x” ，这个问题，对于任意满足C(x)的x，如果所有的x’ > x 也满足C（x’）的话，这个问题可以想像成一个特殊的单调函数，在s的一侧不合法，在s的另一侧不合法，我们就可以用二分法找到某得分界点。

查找满足 <=x 的范围中的最大的一个。

实数区域上的二分

确定好精度 以 L + esp < R 为循环条件 ,一般需要保留2位小数时候，则取精度eps = le-4

while（ L+ esp  < R） 
     double  mid =  (L + R) /2
     if (   ) R = middle
     else   L = middle

   

或者干脆采用循环固定次数的方法，也是不错的策略

for(int i=0; i<100; i++) 
	double middle = (L+R) /2;
	if(  )  L=middle;
	else R =middle