基于相空间重构的混沌背景下微弱信号检测方法仿真

Posted 2022-01-14 fpga&matlab

1.1算法参数取值对系统性能的影响

        在研究算法性能之前，首先需要分析各个参数对算法整体性能的影响，本文将重点考虑相空间重构参数和m，SVM支持向量机参数C和。这里分别对四个参数进行性能影响测试，首先对延迟参数进行分析，其仿真结果如下所示：

 

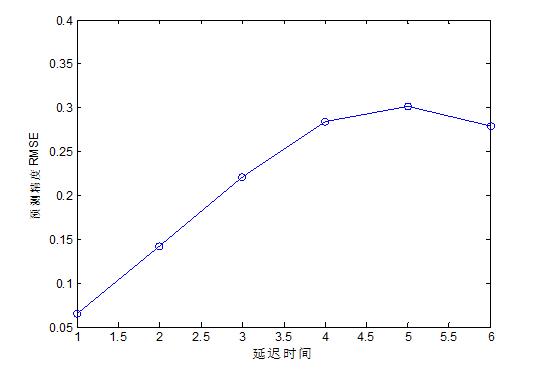
图1 延迟参数对系统预测性能的影响仿真分析

        从图1的仿真结果可知，随着延迟时间的增加，系统性能基本上呈现逐渐降低。但是当延迟时间大于5的时候，性能性能又出现了一定程度的提升。因此，该参数和性能性能并不是线性变化的关系。

 

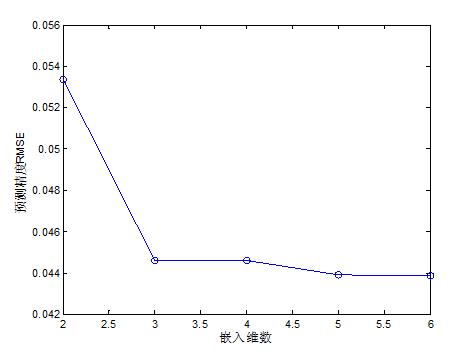
图2 嵌入维数对系统预测性能的影响仿真分析

        从图2的仿真结果可知，随着嵌入维数的增加，系统性能基本上呈现逐渐提升。但当嵌入维数大于3的时候，系统的性能基本保持平稳状态。

 

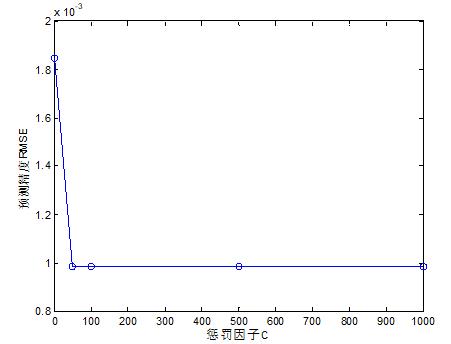
图3 惩罚因子对系统预测性能的影响仿真分析

        从图3的仿真结果可知，随着惩罚因子的增加，系统的性能在出现一次提升之后，当惩罚因子大于50的时候，性能基本保持不变。

 

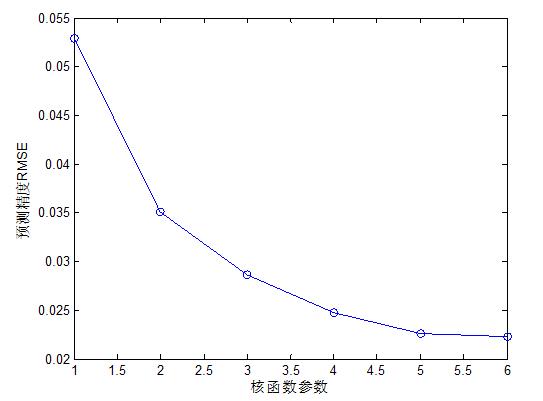
图4 核函数参数对系统预测性能的影响仿真分析

        从图4的仿真结果可知，随着核函数参数的增加，系统的性能在出现了逐渐的提升，随着核函数参数的不断增加，系统性能提升逐渐变缓。

        从上面对四个参数的对比仿真分析可知，四个参数对系统性能影响并不是满足线性关系的，四个参数相互之间有着一定程度的相关性，因此，采用传统的单个参数分析的方法并不能获得最优的参数设置。针对这个问题，本文将分别提出一种基于PSO优化参数和SVM的预测方法以及一种基于GA+PSO改进优化算法和SVM的预测方法。

1.2混沌背景下微弱瞬态信号的检测方法仿真与分析

         首先，对于SVM算法的预测效果进行测试，通过人工任意设置四个参数（2，3，300.9962，2.93），并在481点到520点加入一个幅度为0.0004的随机的瞬间信号，然后使用SVM算法进行预测，其仿真结果如下图所示：

 

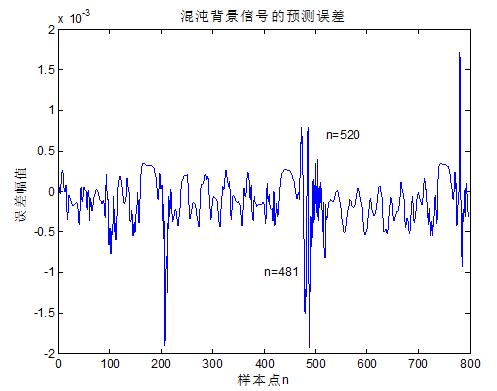
图5 基于SVM算法的微弱瞬态信号检测仿真

        从图5的仿真结果可知，预测误差的整体RMSE值在10的-3次左右，在不考虑参数优化的情况下，通过任意设置参数的方式，其预测结果较差，上图仿真结果中，200点，780点均出现了错误的检测结果，从而因此错误预测。由此可见，通过参数优化对预测效果的提升有着决定性的作用。

​

 

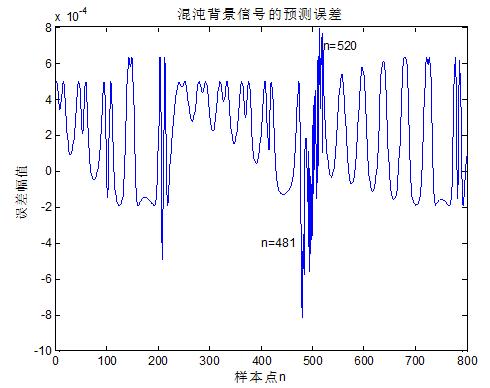
图6 基于PSO优化的SVM算法的微弱瞬态信号检测仿真

        从图6的仿真结果可知，预测误差的整体RMSE值在10的-4次左右，且改善了部分区域干扰的影响，上图中，200点的干扰信号已经小于481点和520点的幅度，在481点到520点的区域出现了较大的幅度，说明瞬时微弱信号的存在，总体而言，通过PSO优化之后，系统的预测性能得到了明显的改善。

         下面对通过GAPSO联合优化参数的SVM进行对含有微弱瞬态信号的混沌背景信号进行预测，通过GAPSO优化，获得（2，2，551.6683，0.2098），获得如下的仿真结果：

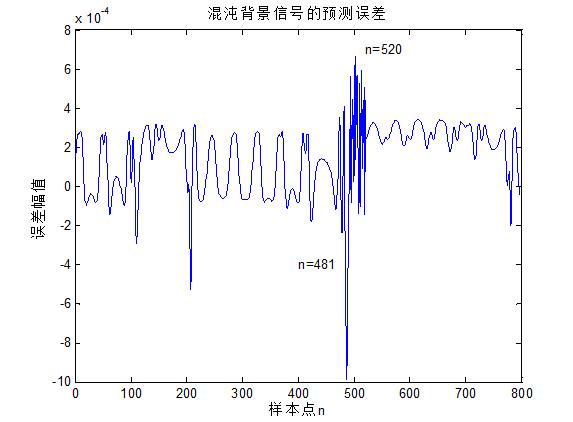
图7基于GAPSO优化的SVM算法的微弱瞬态信号检测仿真

        从图7的仿真结果可知，预测误差的整体RMSE值在10的-4次左右，且改善了部分区域干扰的影响，上图中，在481点到520点的区域出现了较大的幅度，说明瞬时微弱信号的存在。在481点和520点的幅度相对于其余误差信号的幅度明显大于基于PSO优化，总体而言，通过GAPSO优化之后，系统的预测性能得到了明显的改善，且性能优于基于PSO优化的SVM预测算法。

表1 三种算法微弱信号的检测结果对比

	瞬态信号检测RMSE	周期信号检测RMSE
SVM	3.3310e-04	0.0014
PSO+SVM	3.2514e-04	3.7837e-04
GAPSO+SVM	2.2683e-04	2.5819e-04

从三种算法的RMSE值对比可知，GAPSO+SVM算法性能最优。

clc;
clear;
close all;
warning off;
addpath 'func\\'
addpath 'func_SVM_toolbox\\'
addpath 'func_SVM_toolbox\\java\\'
addpath 'func_SVM_toolbox\\java\\libsvm\\'
addpath 'func_SVM_toolbox\\matlab\\'
addpath 'func_SVM_toolbox\\matlab-implement[by faruto]\\'
addpath 'func_SVM_toolbox\\python\\'
addpath 'func_SVM_toolbox\\svm-toy\\'
addpath 'func_SVM_toolbox\\tools\\'
addpath 'func_SVM_toolbox\\windows\\'
%作为对比，直接通过SVM算法，没有通过优化算法直接进行算法的仿真；

%四大参数%参数为人工的任意的设置方式产生
tao   = 2;
m     = 3;
C     = 300.9962;
gamma = 2.93;

%导入数据
load 训练\\X_train.mat;
load 测试\\X_test.mat;

X_train0 = X_train;
X_test0  = X_test;

figure;
plot(X_test0);
xlabel('样本点n');
ylabel('幅值');

[y1,input1ps] = mapminmax(X_train0');
[y2,input2ps] = mapminmax(X_test0');
X_train       = y1';
X_test        = y2';
 
%先进行相空间重构
[Xn ,dn ] = func_CC(X_train,tao,m);
[Xn1,dn1] = func_CC(X_test,tao,m);

 
t  = 1/1:1/1:length(dn1)/1;
f  = 0.05;
sn = 0.0002*sin(2*pi*f*t);
%叠加
dn1 = dn1 + sn';
 
%SVM训练%做单步预测
cmd = ['-s 3',' -t 2',[' -c ', num2str(C)],[' -g ',num2str(gamma)],' -p 0.000001']; 
model = svmtrain(dn,Xn,cmd);
%SVM预测
[Predict1,error1] = svmpredict(dn1,Xn1,model);
RMSE              = sqrt(sum((dn1-Predict1).^2)/length(Predict1));
Err               = dn1-Predict1;
%误差获取
clc;
RMSE 
 

figure;
plot(Err,'b');
title('混沌背景信号的预测误差'); 
xlabel('样本点n');
ylabel('误差幅值');

Fs = 1;
y  = fftshift(abs(fft(Err)));
N  = length(y)
fc = [-N/2+1:N/2]/N*Fs;

figure;
plot(fc(N/2+2:N),y(N/2+2:N));
xlabel('归一化频率');
ylabel('频谱');
text(0.06,0.07,'f=0.05Hz');

  

A-07-06