推荐系统笔记：基于潜在因子模型的协同过滤（latent factor model）

Posted 2022-01-12 UQI-LIUWJ

1 基本思想

        基本思想是利用评分矩阵行和列的高度相关性。数据具有内在的丰富关联性，并且生成的数据矩阵通常可以通过各条目均有数值的低秩矩阵很好地近似。

        潜在因子模型被认为是推荐系统中的最新技术。这些模型利用众所周知的降维方法来填充缺失的条目。

        降维方法通常用于数据分析的其他领域，以在少量维度中表示底层数据。

        降维方法的基本思想是旋转坐标轴，从而消除维度之间的成对相关性。

        降维方法的关键思想是可以从不完整的数据矩阵中稳健地估计维度减少的、旋转的和完全指定的表示。一旦获得了完全指定的表示，就可以将其旋转回原始轴系以获得完全指定的表示 。

        矩阵分解方法提供了一种巧妙的方法，可以同时利用行和列的相关性来估计整个数据矩阵。

2 从几何角度理解LFM

        从集合角度理解就是找到一组潜在向量，组成一个超平面，该超平面可以很好地代表观测点。

         假设一个电影评级场景，其中三个项目对应于尼禄、角斗士和斯巴达克斯这三部电影。

        为便于讨论，假设评级是连续值，位于 [−1, 1] 范围内。假设评分是正相关的，那么评分的 3 维散点图可能大致沿一维线排列，如图 3.6 所示

         由于数据大多沿一维线排列，这意味着去除噪声变化后原始数据矩阵的秩约为 1。例如，图 3.6 的秩 1 近似值将是穿过数据中心并与拉长的数据分布对齐的一维线（或潜在向量）。

        诸如主成分分析 (PCA) 和（以均值为中心的）奇异值分解 (SVD) 等降维方法通常将数据沿这条线的投影表示为近似值。

        当 m × n 评级矩阵的秩为 p （p远小于minm, n 时）（去除噪声变化后），数据可以近似表示在 p 维超平面上。

        在这种情况下，只要 p 维超平面已知，通常可以使用少至 p 个指定条目来稳健地估计用户的缺失评分。例如，在图 3.6 的情况下，只需指定一个评级即可确定其他两个评级，因为评级矩阵在去除噪声后的秩仅为 1。

        例如，如果斯巴达克斯的评分固定为 0.5，那么尼禄和角斗士的评分可以估计为一维潜在向量与轴平行超平面的交集，这个超平面如图 3.6 所示。

       实际上，不需要条目完整的数据矩阵来估计主要的潜在向量。估计具有缺失数据的矩阵的潜在向量的能力是潜在因子方法成功的关键。

        所有这些方法的基本思想是找到一组潜在向量，其中数据点（代表用户对每个item都有评分）与这些潜在向量张成的超平面的平均平方距离尽可能小。

        因此，我们必须使用部分指定的数据集来恢复数据近似所在的低维超平面。通过这样做，我们可以隐式地捕获数据相关结构中的潜在冗余，并一次性重建所有缺失值。正是这些隐含冗余的知识帮助我们预测矩阵中缺失的条目。值得注意的是，如果数据没有任何相关性或冗余性，那么潜在因子模型将根本不起作用。

 3 从代数角度理解LFM

        我们先考虑所有条目都有数值的一个m×n 维矩阵R，它的秩为k，k远小于minm,n。那么R可以分解为m×k维的矩阵U和n×k维的矩阵V的乘积（U和V的每一列可以分别看作矩阵R行向量空间和列向量空间的基，另一个矩阵可以看作是这组基张成矩阵R时的系数）

        

        即使R的秩大于k，R也可以用秩为k的U和V矩阵近似 ，此时误差是残差矩阵的Frobenius 范数||||^2

        那么矩阵分解的含义是什么，它对行和列高度相关的矩阵的影响是什么？

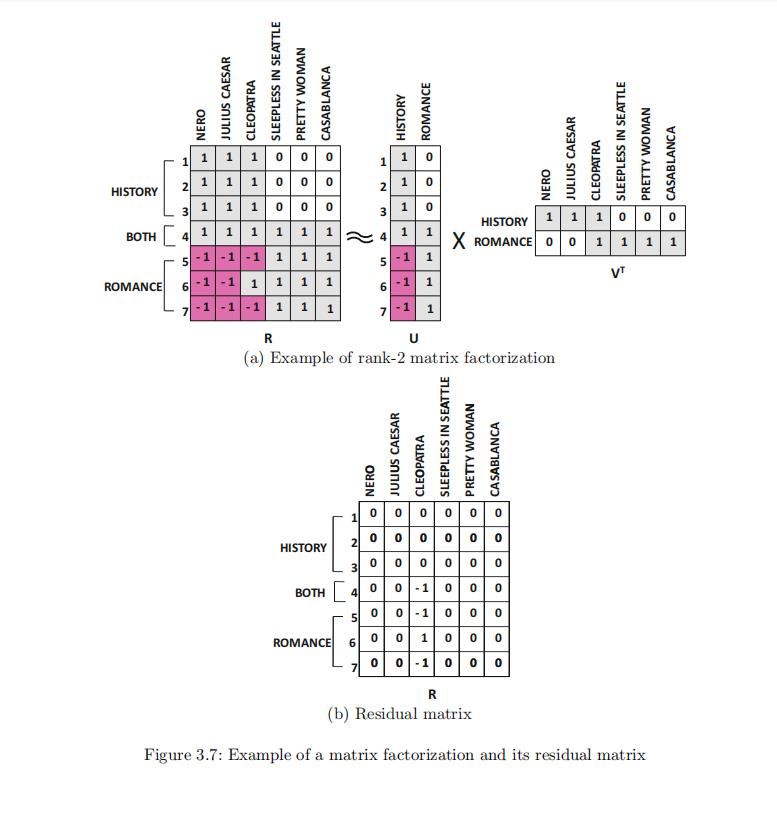
         我们考虑一个这样的矩阵分解案例，7个用户6部电影，打分的可选集合为1,-1,0。

        六部电影从语义上有两个分类：浪漫类和历史类，其中电影Cleopatra两个分类都属于。        

        每个用户对喜欢电影的类型都有自己的偏好（比如用户1喜欢历史类，用户4都喜欢）

         我们可以看到此时矩阵R的某些行/某些列 有着很高的关联度。（比如列向量的电影中，属于历史类的电影之间，属于浪漫类的电影之间【但不同类的电影之间可能就没有多少关联度，这个也很直观】）

        于是打分矩阵R可以分解成矩阵U和矩阵V的乘积形式。这两个矩阵都有着很明显的语义信息：

        U矩阵表示了不同用户对于两类电影的偏好程度；V矩阵表示了不同电影属于的类别

        与此同时我们也计算量残差矩阵，可以看到只有 Cleopatra这一列对应的条目非零。这也很好理解：Cleopatra属于两个类别，和前面的单独浪漫类电影/单独历史类电影不一样。

         在这个例子中，矩阵 R 中的每个条目都具有数值，因此从缺失值估计的角度来看，分解并不是特别有用。

        当矩阵 有缺失条目时，该方法的关键有用性就出现了，但仍然可以分别稳健地估计潜在因子 U 和 V 的所有条目。这仍然可以从稀疏的数据中得到。 一旦矩阵 U 和 V 被估计出来，整个评分矩阵就可以一次被估计出来。

         需要指出的是，U,V的行/列 通常在语义上是不可解释的，做不到像上述3.7一样。 潜在向量通常可能是正值和负值的任意向量，并且很难对其进行语义解释。 然而，它确实代表了评分矩阵中的主要相关联模式。

      某些形式的分解，例如非负矩阵分解，会被明确设计为 为潜在向量实现更大的可解释性。

        各种矩阵分解方法之间的主要区别在于对 U 和 V 施加的约束（例如，潜在向量的正交性或非负性）和目标函数的性质（例如，最小化 Frobenius 范数或最大化似然 生成模型中的估计）。 这些差异对矩阵分解模型在各种现实场景中的可用性起着关键作用。