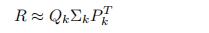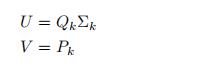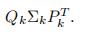推荐系统笔记：基于SVD的协同过滤

Posted 2022-01-14 UQI-LIUWJ

1 奇异值分解

        奇异值分解(SVD)是矩阵分解的一种形式，其中U和V的列被约束为相互正交

        相互正交的优点是概念之间可以完全独立，并且可以用散点几何解释它们。

        然而，这种分解的语义解释通常比较困难，因为这些潜在的向量包含正的和负的量，并且受到它们与其他概念的正交性的限制。

        对于完全指定的矩阵，利用特征分解方法进行奇异值分解是比较容易的。

        考虑一个完全指定的矩阵R，可以使用如下方式来近似R（截断SVD）：

        

        其中k远小于 minm,n（R的维度）

        和分别是和 最大的k个特征值对应的特征向量组成的矩阵，是 （或者说）的最大的k个特征值的平方根组成的对角矩阵

         换句话说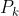，包含了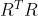 最大特征值对应的那些特征向量，这是行空间的降维近似 所需的基。

        则表示在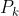的基下，原始矩阵R的表示。

2 奇异值分解—>矩阵分解

        于是我们可以把奇异值分解看成矩阵分解：

        （是一个对角矩阵，不会改变U各列向量的正交性质） 

        此时我们也是用来预测观测矩阵R，只不过此时用户矩阵U和项目矩阵V各自的行向量两两正交。换言之，只要U和V各自的行向量两两正交，我们也可以将矩阵分解改写成SVD分解的形式。

        于是，SVD分解的目标函数可以写成 

         很容易看出，SVD分解与无约束因子分解情况的唯一区别是SVD分解存在正交约束。

        换句话说，与无约束矩阵分解相比，SVD分解使用相同的目标函数，但是在更小的解空间中被优化。

        虽然看起来正交约束的存在会增加误差近似的J。事实证明, 如果R矩阵是完全指定的，且不使用正则化的话，SVD分解和无限制的矩阵分解得到的最优目标J值是相同的。因此，对于完全指定的矩阵，奇异值分解的最优解是无约束矩阵分解的备选最优解之一。

        在R没有完全指定的情况下，这并不一定是真的，目标函数J 仅在有观测的项上计算。在这种情况下，无约束矩阵分解通常会对观察到的条目提供较低的误差。然而，由于不同模型的可泛化程度不同，对未观测条目的相对性能的优劣可能是不可预测的。

 3 简单的使用SVD进行 协同过滤的方法

        在本小节中，我们讨论如何解决矩阵 R 不完全指定时的情况。这是一种最简单的方法

        第一步是通过减去用户 i 的平均评分 μi 来平均居中 R 的每一行。 这些逐行平均值需要存储下来，因为最终将需要它们再加回到对应行的元素中，来重建缺失条目的原始评分。

        令剧中后的矩阵由 Rc 表示。 然后，将 Rc 的缺失条目设置为 0。（将缺失条目设置为相应用户目前的平均评分）

        然后将 SVD 应用于 Rc 以获得 分解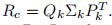。 由此产生的用户矩阵和项目矩阵由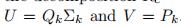给出。

        设 U 的第 i 行是 k 维向量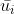，V 的第 j 行是k 维向量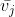。 然后，用户 i 对项目 j 的评分 rij 估计为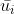和 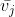的点积，加上均值μi：

4  改进：迭代SVD

        这种方法的主要问题是用逐行均值替换缺失的条目会导致相当大的偏差。

推荐系统笔记： 基于邻居的协同过滤问题 中的降维_UQI-LIUWJ的博客-CSDN博客

       

        不同于那一章节，此时我们可以用另一种迭代的方法来解决这个问题，该方法通过改进对缺失条目的估计来迭代地减少偏差。 该方法使用以下步骤：

（1） 初始化

        将 R 的第 i 行中缺失的条目初始化为该行的均值 μi 以创建 Rf 。

  (2) 迭代步骤

        （2.1）迭代步骤1：对Rf进行svd分解，用前k大的特征值近似Rf，

        （2.2）用2.1得到的 来更新 R中的缺失值

重复（2），直到收敛为止

        当缺失条目的数量很大时，该方法可能会陷入局部最优。（收敛时的局部最优可能对初始化的选择很敏感。）

        我们可以使用推荐系统笔记：无任何限制的矩阵分解_UQI-LIUWJ的博客-CSDN博客中所述的方法，先学习到一个初始的B矩阵。然后有观测值的条目减去相应的 ，然后用0初始化未观测值。 这种方法会得到一个更很好的结果，因为它初始化的方式相对来说更合理一些。

 5 投影梯度下降法

        迭代方法非常昂贵，因为它适用于完全指定的矩阵。 对于较小的矩阵很容易实现，但在大规模设置中不能很好地扩展。

        一种更有效的方法是在前面部分的优化模型中添加正交性约束。  令 S 为评级矩阵中指定条目的集合。 优化问题（带正则化）表述如下：

        该模型与无约束矩阵分解的主要区别在于增加了正交性约束，这使得问题更加困难。

        可以使用投影梯度下降方法，其中 U 或 V  某一列中的所有元素一次更新。 在投影梯度下降中，U（或 V ）的第 p 列的更新后的方向，投影在与 前(p-1)列正交的方向上

         和 推荐系统笔记：无任何限制的矩阵分解_UQI-LIUWJ的博客-CSDN博客 中第五小节一样，也是逐列逐列第更新。但不同的是，如果更新后的这一列不和前面的(p-1)列垂直，那么我们可以找到和前面(p-1)列垂直，同时离更新至最近的点，作为投影梯度下降法的更新值。

        

比如假设我们已经更新得到了u1和u2，它们是正交的。我们现在通过增量潜在因子训练，得到了u3，但是u3和u1,u2张成的平面不垂直。于是我们找u3的投影，作为u3的更新值

 6 外推推荐 out-of-sample recommendation

        许多矩阵完成方法（如矩阵分解）只能对训练时已包含在评分矩阵中的用户和项目进行预测。

        如果在分解时未将新用户和项目包含在原始评分矩阵 R 中，则从因子 U 和 V 对新用户和项目进行预测通常并不容易。

        正交基向量的一个优点是可以更轻松地利用它们为新用户和项目执行样本外推荐。 这个问题也被称为归纳矩阵完成。

        推荐系统笔记：基于潜在因子模型的协同过滤（latent factor model）中提供的几何解释有助于理解为什么正交基向量有助于预测缺失的评分。

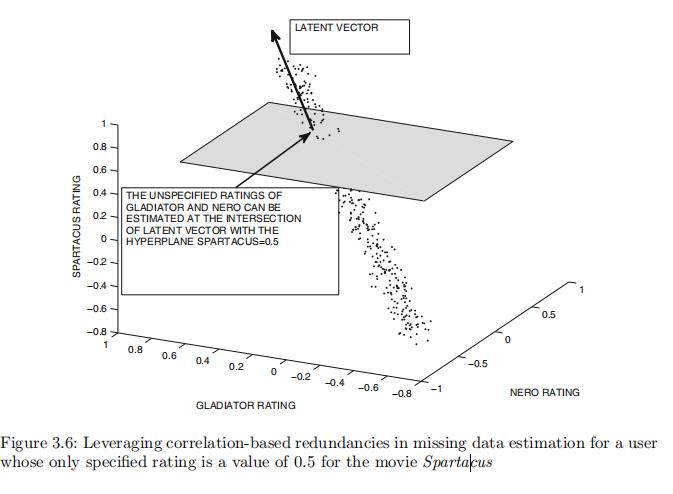
一旦获得了潜在向量，就可以将指定评分中的信息投影到相应的潜在向量上； 当向量相互正交时，这要容易得多。 考虑 SVD 分别获得潜在因子 U 和 V 的情况。 V 的列（基））定义了一个通过原点的 k 维超平面 H1。

        在图 3.6 中，潜在因子的数量为 1，因此显示了单个潜在向量（即一维向量）。 基有两个因子组成，它就会是二维平面。  

        现在想象一个新用户的评分已添加到系统中。 请注意，此新用户未在 U 或 V 中的潜在因子中表示。

        考虑新用户指定了总共 h 个评分的场景。 该用户未评分的这些电影的评分可能性空间是一个 (n - h) 维的超平面。

         图 3.6 展示了一个例子，其中斯巴达克斯的一个电影的打分是固定的，超平面定义在其他两个维度上。 让这个超平面用 H2 表示。

         然后目标是确定 H2 上的点，该点尽可能接近 H1。